双因素方差分析原理分析步骤与案例分析

双因素方差分析(ANOVA)是一种用于研究两个分类自变量对一个连续因变量影响的统计方法。下面我将详细介绍其原理、分析步骤，并通过一个实际案例进行演示。

一、双因素方差分析原理

1. 基本概念

双因素方差分析用于研究两个分类自变量(X1和X2)对一个连续因变量(Y)的影响，比单因素方差分析能考虑更多因素对结果的影响。

2. 核心分析内容

• 主效应：单个自变量对因变量的独立影响
• 交互效应：两个自变量共同作用对因变量的影响
• 简单效应：一个自变量在另一个自变量不同水平上的影响
• 事后多重比较：当主效应显著时，比较不同水平间的差异

3. 适用条件

• 因变量为连续变量
• 自变量为两个分类变量
• 数据满足正态性和方差齐性(但方差分析对此有一定稳健性)

二、分析步骤

Step 1: 适用条件判断

1. 检查数据是否符合正态分布和方差齐性要求
2. 结合研究设计和专业经验判断是否考察交互作用

Step 2: 是否考察交互作用

根据研究目的决定是否考察交互作用： 考察交互作用——分析主效应和交互效应；不考察交互作用——仅分析主效应。

Step 3: 效应显著性检验

1. 检验主效应和交互效应的显著性
2. 交互作用显著时优先解读交互作用

Step 4: 进一步分析

• 当主效应显著(p<0.05)时：进行事后多重比较
• 当交互作用显著(p<0.05)时：进行简单效应分析

三、案例分析

案例背景

研究不同施肥方式(A、B、C、D)和不同水稻品种(1、2、3)对产量的影响，以及施肥方式和品种是否存在交互作用。

数据格式

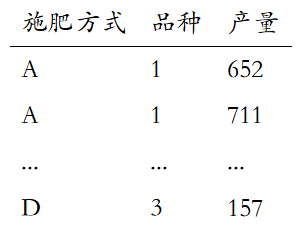
SPSSAU操作步骤

1. 登录SPSSAU(在线SPSS)平台
2. 上传数据后选择【进阶方法】模块"双因素方差分析"
3. 将变量拖拽到相应分析框：
   • 因变量：产量
   • 自变量：施肥方式、品种
4. 勾选【二阶效应】和【简单效应】
5. 事后多重比较选择【LSD】法
6. 点击"开始分析"

结果解读

1. 主效应分析

施肥方式：F=104.962，p=0.000<0.05 → 主效应显著
品种：F=401.889，p=0.000<0.05 → 主效应显著

2. 交互效应分析

施肥方式*品种：F=28.624，p=0.000<0.05 → 交互作用显著

3. 简单效应分析

由于交互作用显著，需要进行简单效应分析，考察： 

- 在不同施肥方式下，品种间的产量差异 

- 在不同品种下，施肥方式间的产量差异

4. 事后多重比较

由于主效应显著，可以进行两两之间事后多重比较，了解： 

- 哪些施肥方式间的产量差异显著 

- 哪些品种间的产量差异显著

四、结论与建议

1. 本案例中施肥方式和品种对产量均有显著影响(主效应显著)
2. 施肥方式和品种存在交互作用，说明不同品种对不同施肥方式的响应不同
3. 建议：
   • 优先关注交互作用分析结果
   • 结合简单效应分析结果，为不同品种选择最优施肥方式
   • 使用SPSSAU(网页SPSS)平台可以轻松完成上述分析

通过双因素方差分析，我们不仅能了解单个因素的影响，还能发现因素间的交互作用，为实际决策提供更全面的依据。