1.二阶系统的调节过程
考虑对于如下所示的二阶系统
{x¨=−a1(x−v0)−a2x˙y=x(1.1)
\begin{cases}
\ddot{x} = -a_1 (x - v_0) - a_{2} \dot{x}\\ \tag{1.1}
y = x
\end{cases}
{x¨=−a1(x−v0)−a2x˙y=x(1.1)
输入单位阶跃信号 v0=1v_0 = 1v0=1时的响应。
希望系统的输出yyy尽可能快的、无超调的跟踪阶跃信号。当a1>0,a2>0a_1>0 ,a_2>0a1>0,a2>0时,该二阶系统可以跟踪输入信号 v0v_0v0,但是过渡过程不一定没有超调和振荡。
对系统方程(1.1)进行拉氏变换:
s2Y(s)−sY(0)−Y′(0)=−a1Y(s)−a2[sY(s)−Y(0)]+a1X(s)s2Y(s)=−a1Y(s)−a2sY(s)+a1X(s)Y(s)[s2+a2s+a1]=a1X(s)
s^2Y(s) - sY(0) - Y^{'}(0) = -a_1Y(s)-a_2[sY(s)-Y(0)]+a_1X(s) \\
s^2Y(s) = -a_1Y(s)-a_2 sY(s)+a_1X(s) \\
Y(s) [s^2+a_2s+a_1] = a_1X(s)s2Y(s)−sY(0)−Y′(0)=−a1Y(s)−a2[sY(s)−Y(0)]+a1X(s)s2Y(s)=−a1Y(s)−a2sY(s)+a1X(s)Y(s)[s2+a2s+a1]=a1X(s)
即可得出该二阶系统传递函数:
Y(s)X(s)=a1s2+a2s+a1(1.2)\frac{Y(s)}{X(s)} = \frac{a_1}{s^2+a_2 s+a_1} \tag{1.2}X(s)Y(s)=s2+a2s+a1a1(1.2)
为了使系统尽可能快且没有超调的跟踪给定的输入阶跃信号,我们设置系统参数使之成为一个临界阻尼的二阶系统。
说明:
1.欠阻尼系统可以使得系统调节时间减少,但是会出现超调和振荡;
2.过阻尼的系统无超调、无振荡,但是调节时间过长;
3.临界阻尼系统系统能在保证尽可能快的跟踪给定的阶跃信号,也可以无超调、无振荡。
因此我们选择适当参数使得该二阶系统为临界阻尼二阶系统。
二阶系统(1.2)的特征方程为:
D(s)=s2+a2s+a1=0(1.3)D(s) = s^2+a_2 s+a_1 = 0 \tag{1.3}D(s)=s2+a2s+a1=0(1.3)
故特征根为:
s1,2=−a2±a22−4a12s_{1,2}= \frac{-a_2 \pm \sqrt {a_2^2-4a_1}}{2}s1,2=2−a2±a22−4a1
若使系统为临界阻尼系统,则
a22−4a1=0,s1,2=−ωna_2^2-4a_1=0,s_{1,2}= -\omega_na22−4a1=0,s1,2=−ωn
即
a2=2a1a_2 = 2\sqrt {a_1}a2=2a1
取a1=r2,a2=2ra_1 =r^2,a_2=2ra1=r2,a2=2r,当r>0r>0r>0时即可保证系统处于临界阻尼状态。
此时系统变为:
{x¨=−r2(x−v0)−2rx˙y=x
\begin{cases}
\ddot{x} = - r^2 (x - v_0) - 2r \dot{x}\\
y = x
\end{cases}
{x¨=−r2(x−v0)−2rx˙y=x
根据二阶系统临界阻尼的特性,我们可以计算出该系统对于单位阶跃响应的调节时间:
在Δ=2\Delta =2Δ=2时,Ts=5.84ωnT_s =\frac{5.84}{\omega_n}Ts=ωn5.84
在Δ=5\Delta =5Δ=5时,Ts=4.75ωnT_s =\frac{4.75}{\omega_n}Ts=ωn4.75
取不同的系统参数r=2,4,6,8r=2,4,6,8r=2,4,6,8,使得系统单位阶跃响应是不同的,matlab仿真如下:
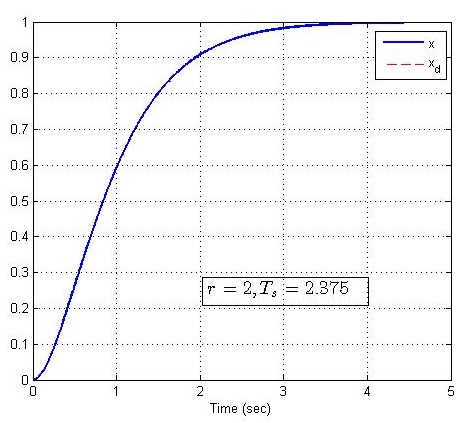
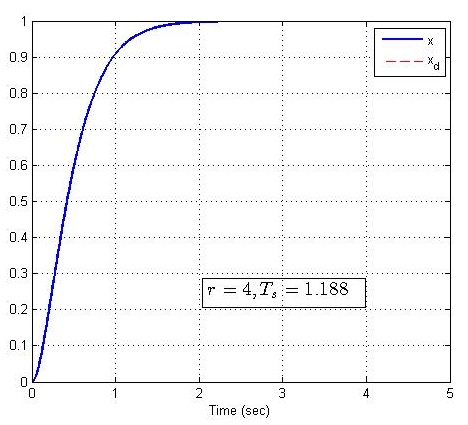
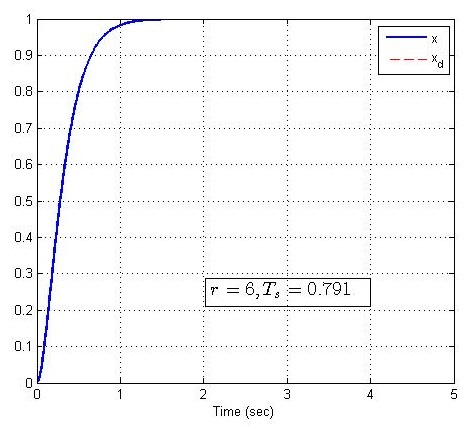
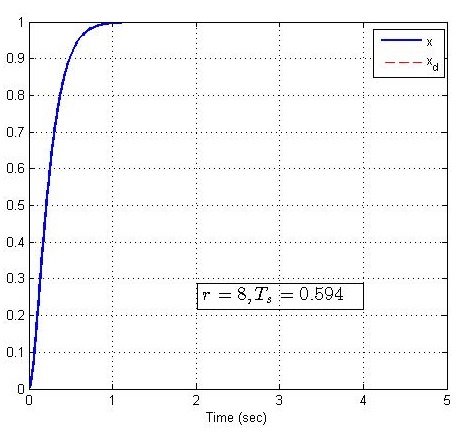
2.加入PD控制的二阶系统调节过程
加入控制器后的系统(1.1)变为
{x¨=−a1x−a2x˙+uy=x(2.1)
\begin{cases}
\ddot{x} = - a_1 x - a_2 \dot{x} + u\\ \tag{2.1}
y = x
\end{cases}
{x¨=−a1x−a2x˙+uy=x(2.1)
取PD控制器
u=k1(v0−x)+k2(v˙0−x˙)=k1(v0−x)+k2(−x˙)u=k_1(v_0 - x)+k_2( \dot{v}_0- \dot{x}) =k_1(v_0 - x)+k_2( - \dot{x})u=k1(v0−x)+k2(v˙0−x˙)=k1(v0−x)+k2(−x˙)
将带入系统方程(2.1),可得
{x¨=−(a1+k1)(x−v0)−(a2+k2)x˙y=x(2.2)
\begin{cases}
\ddot{x} = - (a_1+k_1)(x - v_0) - (a_2 +k_2)\dot{x} \\ \tag{2.2}
y = x
\end{cases}
{x¨=−(a1+k1)(x−v0)−(a2+k2)x˙y=x(2.2)
取a‾1=a1+k1>0,a‾2=a2+k2>0\overline{a}_1 = a_1+k_1>0,\overline{a}_2 = a_2+k_2>0a1=a1+k1>0,a2=a2+k2>0,系统方程(2.2)变为:
{x¨=−a‾1(x−v0)−a‾2x˙y=x(2.3)
\begin{cases}
\ddot{x} = - \overline{a}_1(x - v_0) - \overline{a}_2\dot{x} \\ \tag{2.3}
y = x
\end{cases}
{x¨=−a1(x−v0)−a2x˙y=x(2.3)
为了使闭环系统无超调、无振荡,则需满足
a‾1=r2,a‾2=2r\overline{a}_1 =r^2,\overline{a}_2=2ra1=r2,a2=2r
也就是说,在系统参数a1,a2a_1,a_2a1,a2给定的情况下,控制器参数k1,k2k_1,k_2k1,k2需满足以下关系:
k1=2a1+k1−a2k_1 = 2\sqrt {a_1+k_1} - a_2k1=2a1+k1−a2
系统的特征根为s1,2=−ωn=a‾22s_{1,2}= -\omega_n=\frac{\overline{a}_2}{2}s1,2=−ωn=2a2
当系统参数设定为a1=a2=2a_1=a_2=2a1=a2=2
取PD控制器的控制参数k1=2.0k_1=2.0k1=2.0,为了保证闭环系统为临界阻尼状态,则k2k_2k2需满足:
k2=2a1+k1−a2=24−2=2k_2=2\sqrt {a_1+k_1}-a_2=2\sqrt {4}-2=2k2=2a1+k1−a2=24−2=2.
此时系统的调节时间为
Ts=4.75ωn=4.75a‾2/2=9.5a‾2=9.5a2+k2=2.375T_s=\frac{4.75}{\omega_n}=\frac{4.75}{\overline{a}_2/2}=\frac{9.5}{\overline{a}_2}=\frac{9.5}{a_2+k_2}=2.375Ts=ωn4.75=a2/24.75=a29.5=a2+k29.5=2.375.
matlab仿真如下:
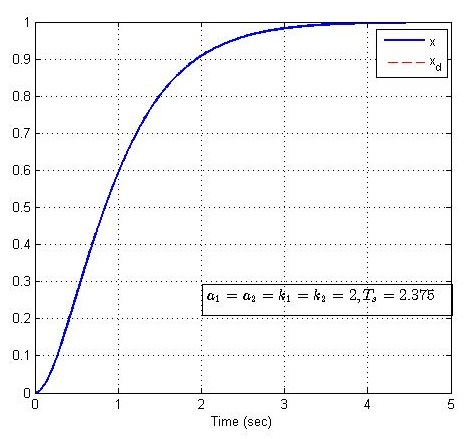
现固定控制器增益k1=k2=2k_1=k_2=2k1=k2=2,分别改变系统参数a1,a2a_1, a_2a1,a2为(3,2),(1,2),(2,3),(3,1),matlab仿真如下:
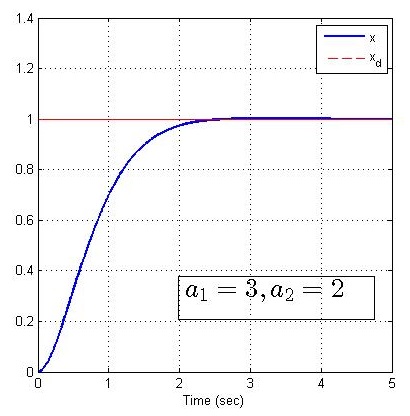
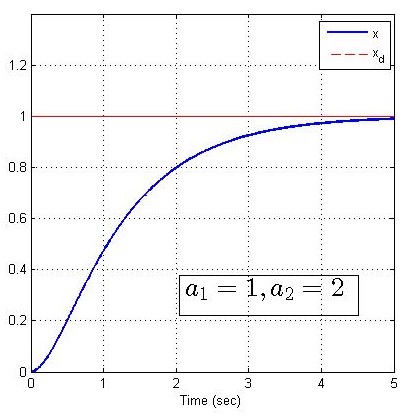
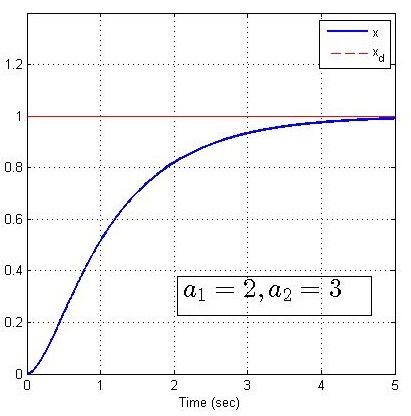
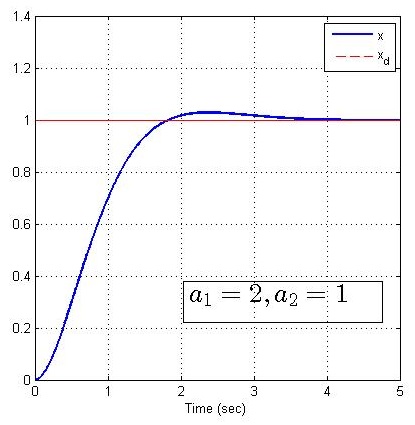
矛盾分析
在阶跃响应中,由于直接取实际输出与期望之间的误差e0=x−v0e_0 = x-v_0e0=x−v0,在系统初始状态下,误差e0=x−v0=−v0e_0 = x-v_0=-v_0e0=x−v0=−v0,为了使系统调节过程加快,取较大的k1k_1k1,但这又容易使闭环系统产生超调。特别是在一些实际生产过程中,系统不允许有超调产生,所以快速性与超调产生矛盾。
若能在初始状态下降低起始误差,那么就可以在不改变系统参数的情况下用较大的增益调节系统,加快过渡过程。
初始误差e0=x−v0e_0 = x-v_0e0=x−v0,无非两种方法,改变初始输出或者改变初始目标,初始输出为0的情况下,改变初始目标值是一种好办法,因此对初始目标值安排过渡过程。
3.加入过渡过程
3.1 加入过度过程的比例控制
定义如下函数:
trns(T0,t)={12(1+sin(π(tT0−12))),t≤T01,t>T0(3.1)
trns(T_0,t) =
\begin{cases}
\frac{1}{2}(1 + sin(\pi(\frac{t}{T_0}- \frac{1}{2}))) , &t \leq T_0\\ \tag{3.1}
1,&t >T_0
\end{cases}
trns(T0,t)={21(1+sin(π(T0t−21))),1,t≤T0t>T0(3.1)
在T0T_0T0时间内,曲线从0单调上升到1并保持不变的曲线,在T0T_0T0时间外,保持1不变。
因此,安排目标过渡过程的P控制后,闭环系统(2.3)变为:
{x¨=−a‾1(x−v0trns(T0,t))−a‾2x˙y=x(3.2)
\begin{cases}
\ddot{x} = - \overline{a}_1(x - v_0trns(T_0,t)) - \overline{a}_2\dot{x} \\ \tag{3.2}
y = x
\end{cases}
{x¨=−a1(x−v0trns(T0,t))−a2x˙y=x(3.2)
先对有无安排过渡过程前后两种情况的仿真结果进行对比,
同样,取不同的系统参数a1=a2=0a_1=a_2=0a1=a2=0,和控制参数k1k_1k1,结果对比如下:取不同
仿真结果对比
(1 无过渡过程 k1=0,3,6k_1=0,3,6k1=0,3,6
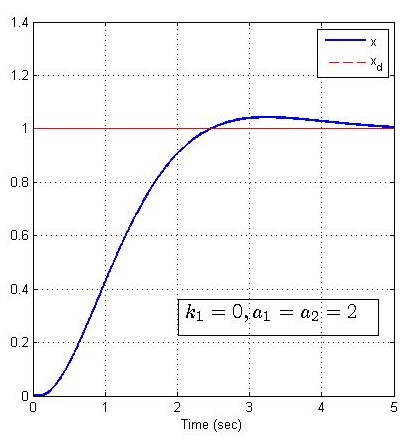
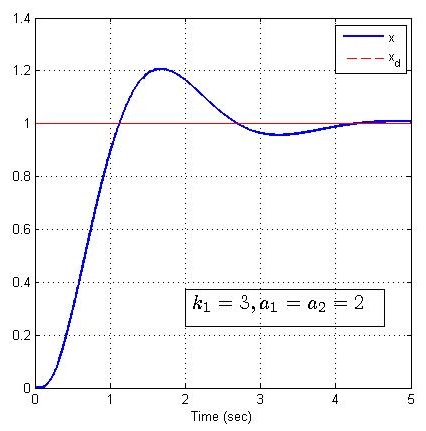
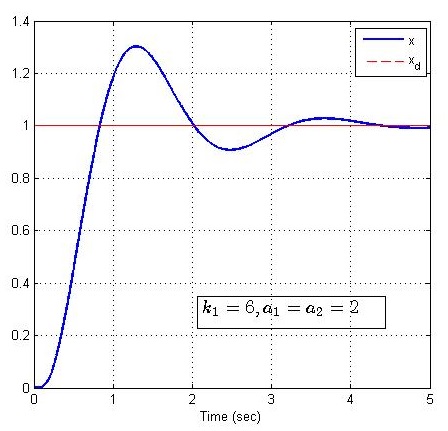
(2 有过渡过程
过渡时间 T0=1T_0 = 1T0=1
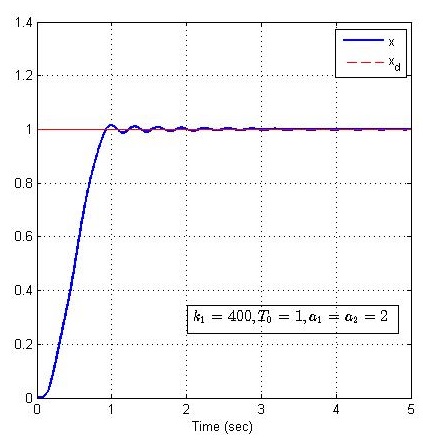
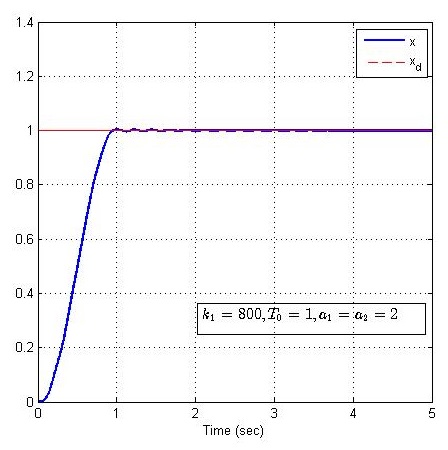
过渡时间 T0=2T_0 = 2T0=2
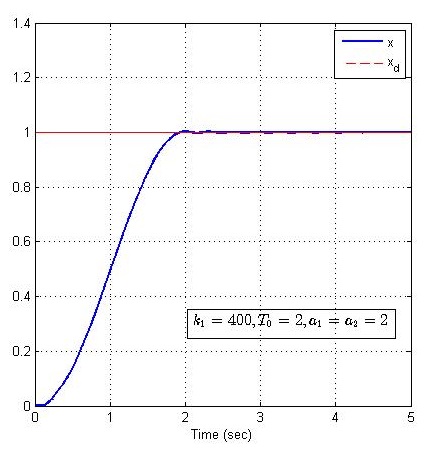
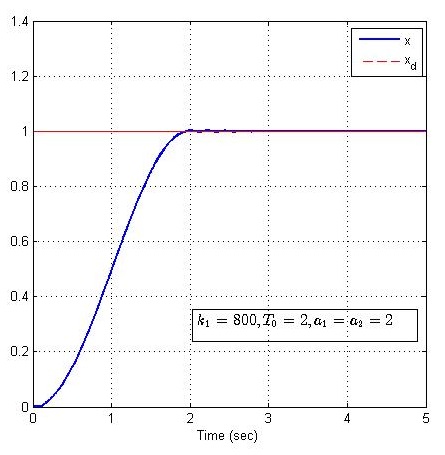
经过对比显示,安排过渡过程,可以在大增益的情况下有效抑制超调产生,并且可以减少调节时间。
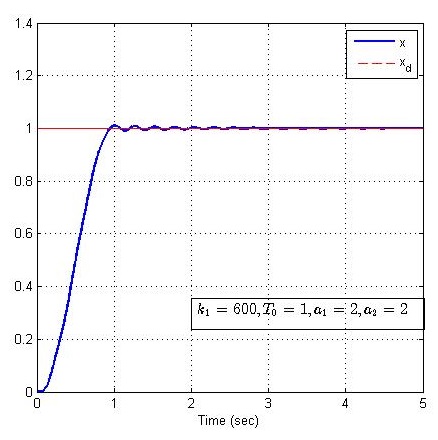
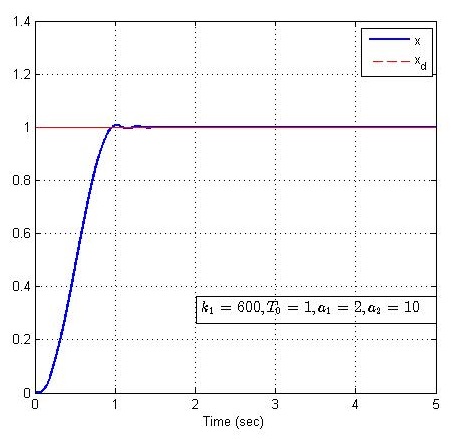
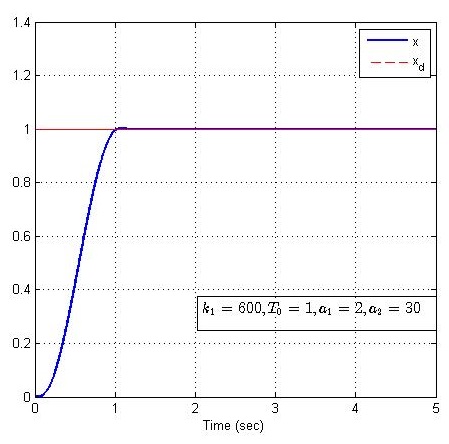
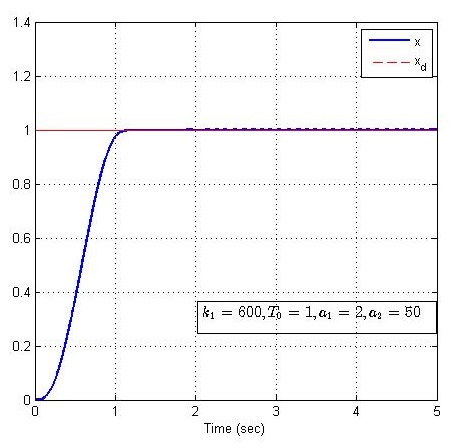
现在探索安排过渡过程的另一个优势,固定控制器参数k1=600k_1 = 600k1=600、系统参数a1=2a_1 = 2a1=2和过渡时间T0=1T_0 = 1T0=1,改变系统参数a2=2,10,30,50a_2 = 2,10,30,50a2=2,10,30,50,仿真结果如下:
小结
由上图可以看出,系统参数a2a_2a2变化明显,但未对系统的阶跃响应产生明显影响,说明事先安排过渡过程能够扩大控制系统的适用范围。
3.2 加入过度过程的比例微分控制
由于安排了过渡过程,那么给定目标的v˙0\dot{v}_0v˙0不恒为零,对过渡过程(3.1)进行求导
dtrns(T0,t)={π2T0cos(π(tT0−12)),t≤T01,t>T0(3.3) dtrns(T_0,t) = \begin{cases} \frac{\pi}{2T_0} cos(\pi(\frac{t}{T_0}- \frac{1}{2})) , &t \leq T_0\\ \tag{3.3} 1,&t >T_0 \end{cases} dtrns(T0,t)={2T0πcos(π(T0t−21)),1,t≤T0t>T0(3.3)
因此,PD控制器为
u=k1(v0trns(T0,t)−x)+k2(v˙0dtrns(T0,t)−x˙)u=k_1(v_0trns(T_0,t) - x)+k_2( \dot{v}_0dtrns(T_0,t)- \dot{x})u=k1(v0trns(T0,t)−x)+k2(v˙0dtrns(T0,t)−x˙)
带入二阶系统,闭环的系统方程(3.2)为:
{x¨=−a‾1(x−v0trns(T0,t))−a‾2(x˙−v0dtrns(T0,t))y=x(3.4)
\begin{cases}
\ddot{x} = - \overline{a}_1(x - v_0trns(T_0,t)) - \overline{a}_2(\dot{x}-v_0dtrns(T_0,t)) \\ \tag{3.4}
y = x
\end{cases}
{x¨=−a1(x−v0trns(T0,t))−a2(x˙−v0dtrns(T0,t))y=x(3.4)
取系统参数a1=a2=2a_1 =a_2 =2a1=a2=2,过渡过程时间为T0=0.5T_0 =0.5T0=0.5,改变控制增益,仿真结果如下:
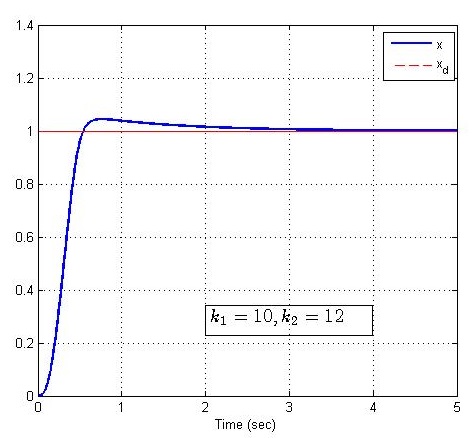
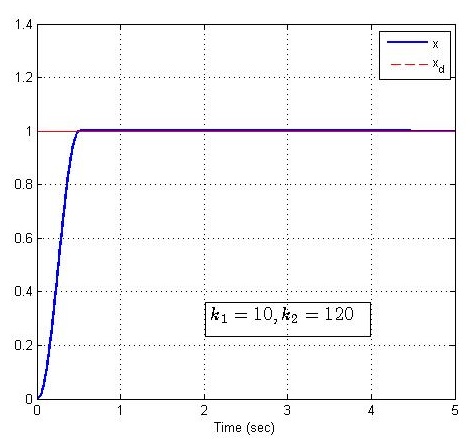
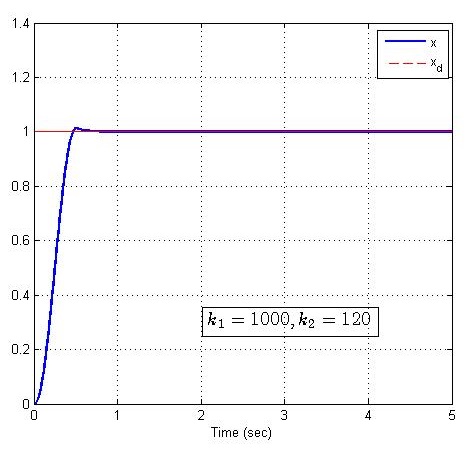
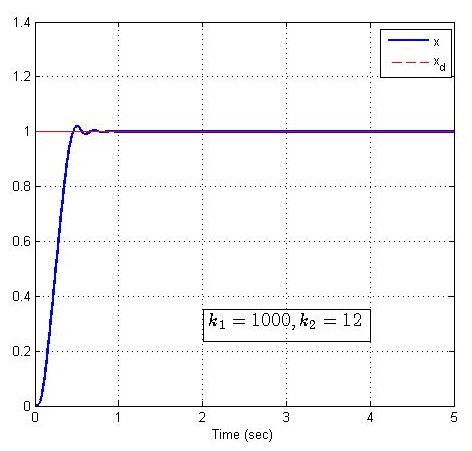
小结
上图仿真表明,PD控制增益在大范围内的不同选取,对过渡过程特性的影响并不大,同样也说明,在这个范围内给定的PD控制增益所能适应的系统参数a1a2a_1 a_2a1a2的范围也很大。
总结
- 事先安排过渡过程是解决超调与快速性矛盾的一种很有效的办法;
- 事先安排过渡过程使误差反馈增益和误差微分反馈增益的选取范围大为扩大,便于控制系统的参数整定;
- 事先安排过渡过程使给定的控制增益所能适应的对象参数范围大为扩大,控制器的鲁棒性更为加强。
参考文献:韩京清 《自抗扰控制技术——估计补偿不确定因素的控制技术》







 本文探讨了二阶系统在调节过程中的表现,分析了加入PD控制后系统的变化。通过仿真展示了加入过渡过程如何在不增加超调的情况下加快调节速度。同时,研究了比例和比例微分控制在有过渡过程时的效果,证明了预先安排过渡过程能提高控制系统适应性和鲁棒性。
本文探讨了二阶系统在调节过程中的表现,分析了加入PD控制后系统的变化。通过仿真展示了加入过渡过程如何在不增加超调的情况下加快调节速度。同时,研究了比例和比例微分控制在有过渡过程时的效果,证明了预先安排过渡过程能提高控制系统适应性和鲁棒性。
















 818
818

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








