正文详见：
5.1 动手实现一个 LLaMA2 大模型
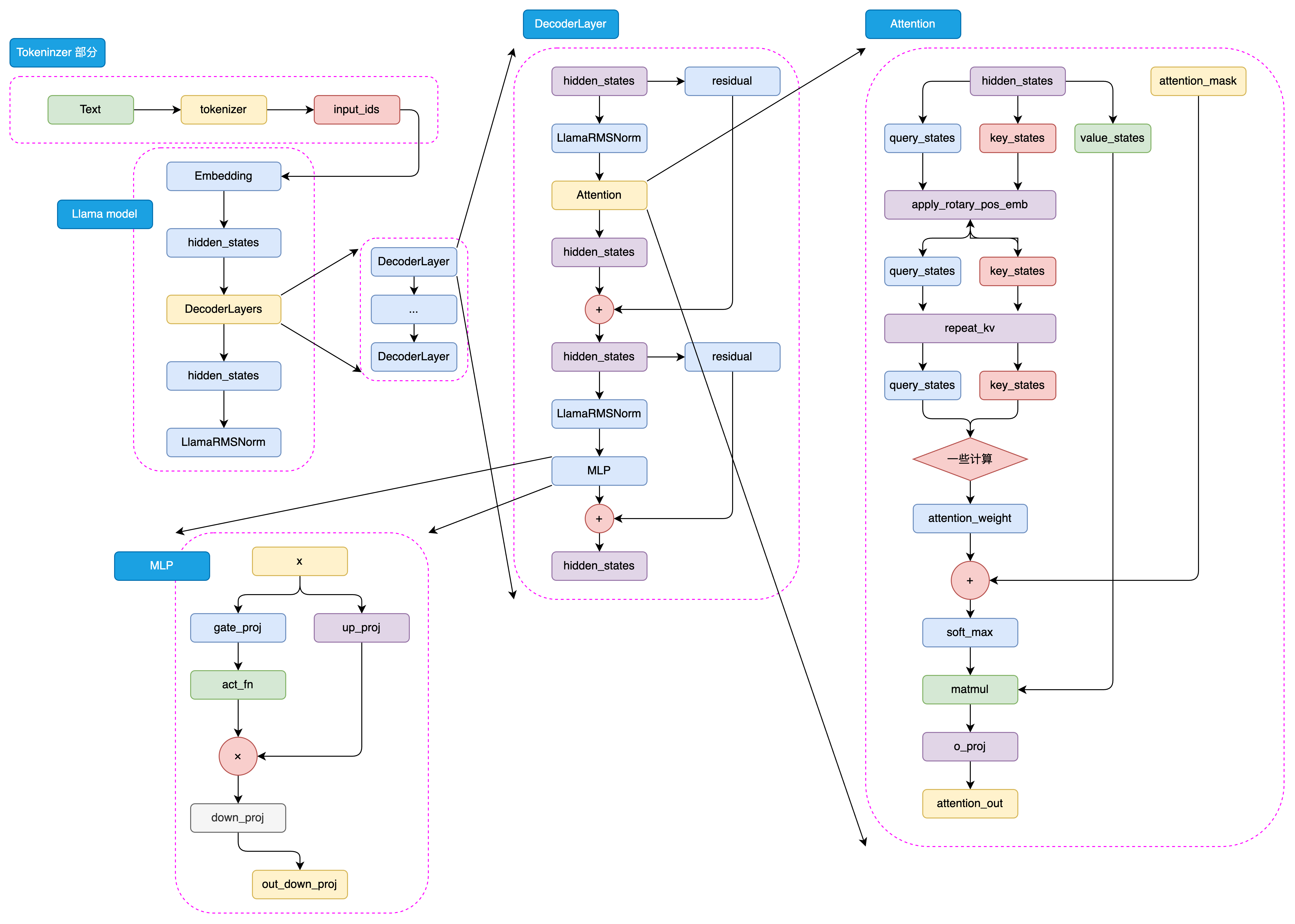
5.1.1 定义超参数
自定义一个ModelConfig类用来记录和存储超参。
# 使用transformers库中的PretrainedConfig
from transformers import PretrainedConfig
class ModelConfig(PretrainedConfig):
model_type = "Tiny-K"
def __init__(
self,
dim: int = 768, # 模型维度
n_layers: int = 12, # Transformer的层数
n_heads: int = 16, # 注意力机制的头数
n_kv_heads: int = 8, # 键值头的数量
vocab_size: int = 6144, # 词汇表大小
hidden_dim: int = None, # 隐藏层维度
multiple_of: int = 64,
norm_eps: float = 1e-5, # 归一化层的eps
max_seq_len: int = 512, # 最大序列长度
dropout: float = 0.0, # dropout概率
flash_attn: bool = True, # 是否使用Flash Attention
**kwargs,
):
self.dim = dim
self.n_layers = n_layers
self.n_heads = n_heads
self.n_kv_heads = n_kv_heads
self.vocab_size = vocab_size
self.hidden_dim = hidden_dim
self.multiple_of = multiple_of
self.norm_eps = norm_eps
self.max_seq_len = max_seq_len
self.dropout = dropout
self.flash_attn = flash_attn
super().__init__(**kwargs)5.1.2 构建 RMSNorm
Layer Norm 要计算标准差，计算量较大，且涉及减法操作，可能影响数值稳定性。
RMSNorm数学公式为：
class RMSNorm(nn.Module):
def __init__(self, dim: int, eps: float):
super().__init__()
# eps是为了防止除以0的情况，对应公式里的ϵ
self.eps = eps
# weight是一个可学习的参数，全部初始化为1，对应公式里的γ
self.weight = nn.Parameter(torch.ones(dim))
def _norm(self, x):
# 计算RMSNorm的核心部分
# x.pow(2).mean(-1, keepdim=True)计算了输入x的平方的均值
# 再加上eps防止分母为0
# torch.rsqrt是平方根的倒数
# 这样就得到了RMSNorm的分母部分
# 最后乘以x，得到RMSNorm的结果
return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
def forward(self, x):
# forward函数是模型的前向传播
# 首先将输入x转为float类型，然后进行RMSNorm，最后再转回原来的数据类型
# 最后乘以weight，这是RMSNorm的一个可学习的缩放因子
output = self._norm(x.float()).type_as(x)
return output * self.weight5.1.3 构建 LLaMA2 Attention
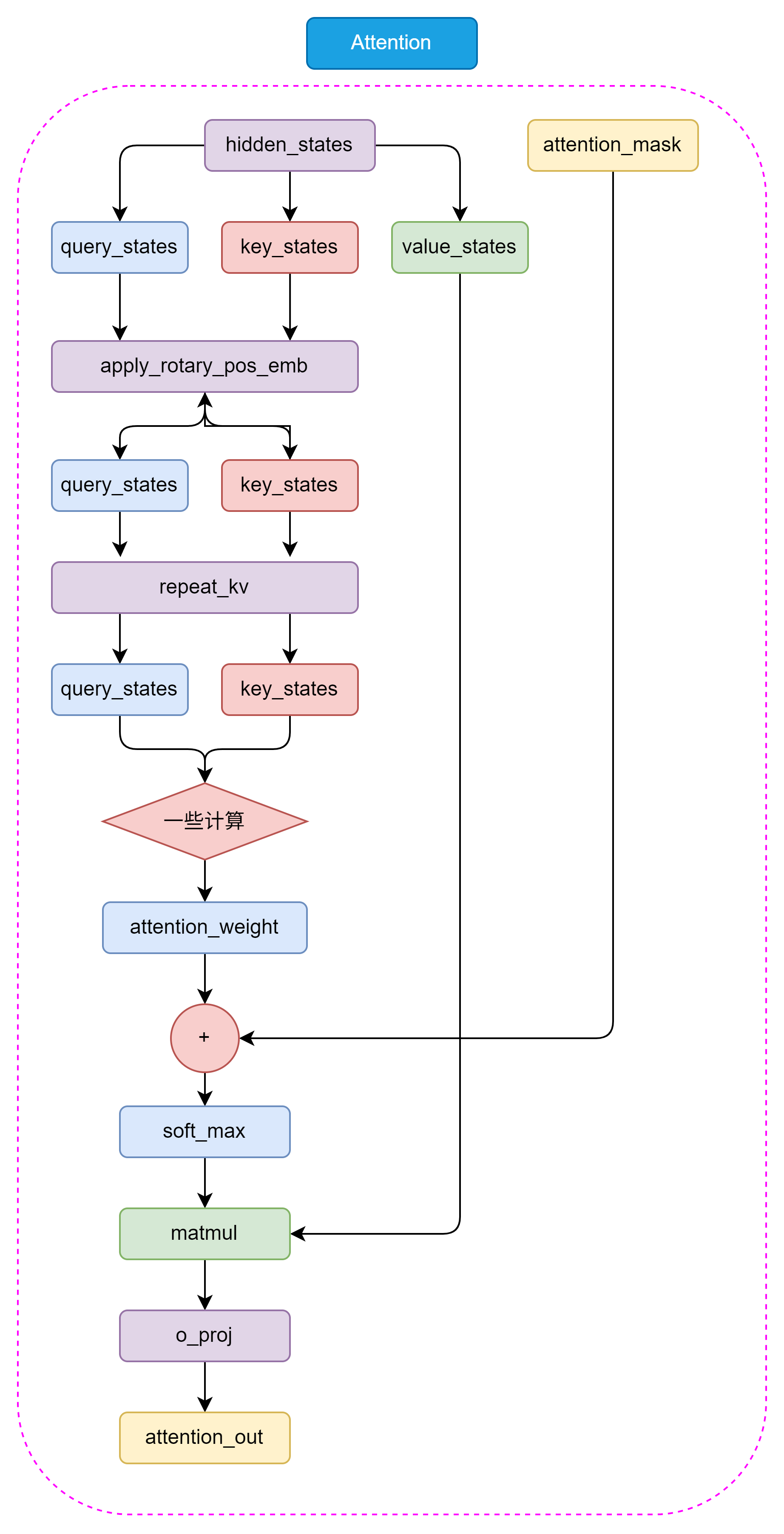
LLaMA2-70B模型使用了分组查询注意力机制（Grouped-Query Attention，GQA）构建 LLaMA Attention 模块，它可以提高模型的效率，并节省一些显存占用。
5.1.3.1 repeat_kv
通过 repeat_kv 函数， 将键和值的维度扩展到和查询的维 度一样，这样才能进行注意力计算。
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
# 获取输入张量的形状：批量大小、序列长度、键/值对头的数量、每个头的维度大小
bs, slen, n_kv_heads, head_dim = x.shape
# 如果重复次数为1，则不需要重复，直接返回原始张量
if n_rep == 1:
return x
# 对张量进行扩展和重塑操作以重复键值对
return (
x[:, :, :, None, :] # 在第四个维度（头的维度前）添加一个新的维度
.expand(bs, slen, n_kv_heads, n_rep, head_dim) # 将新添加的维度扩展到n_rep大小，实现重复的效果
.reshape(bs, slen, n_kv_heads * n_rep, head_dim) # 重新塑形，合并键/值对头的数量和重复次数的维度
)5.1.3.2 旋转嵌入
旋转位置编码rope：十分钟读懂旋转编码（RoPE）
https://www.zhihu.com/tardis/bd/art/647109286通俗易懂-大模型的关键技术之一:旋转位置编码rope （3）_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Mj421R7JQ?spm_id_from=333.788.player.switch&vd_source=8fb10652f8c3316e5308e66bcf6011f0旋转位置编码所谓的“旋转”是在词向量维度为二维的条件进行的旋转操作。当词向量的维度扩展到多维（维度数为偶数）时，向量元素则是两两一组进行旋转。注意，两两一组并不用按照维度顺序划分，因为神经元是无序的，所以维度和纬度之间也是无序的，所以只要保证任意一般的向量元素取负号来进行旋转位置编码即可。Chatglm中便将后一半向量元素取负号。
旋转嵌入是 LLaMA2 模型中的一个重要组件，它可以为注意力机制提供更强的上下文信息，从而提高模型的性能。
# 注意：此处的dim应为 dim//n_head，因为我们是对每个head进行旋转嵌入
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
# torch.arange(0, dim, 2)[: (dim // 2)].float()生成了一个从0开始，步长为2的序列，长度为dim的一半
# 然后每个元素除以dim，再取theta的倒数，得到频率
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 生成一个从0到end的序列，长度为end
t = torch.arange(end, device=freqs.device)
# 计算外积，得到一个二维矩阵，每一行是t的元素乘以freqs的元素
freqs = torch.outer(t, freqs).float()
# 计算频率的余弦值，得到实部
freqs_cos = torch.cos(freqs)
# 计算频率的正弦值，得到虚部
freqs_sin = torch.sin(freqs)
return freqs_cos, freqs_sin-
计算频率序列
torch.arange(0, dim, 2)[: (dim // 2)].float() 生成了一个从0开始，步长为2的序列，其长度为dim/2。
除以dim后取theta的倒数，得到一个频率序列 freqs,长度为dim/2。
这一步是为了生成适合旋转嵌入的频率序列freqs={
}。
对于一个query给定长上下文参考，模型输出的结果不应该受到正确答案在文中距离的影响（类似大海捞针任务），也就是不管答案在哪，根据query计算注意力分数时都要保证答案与query的attention score最大，如果attention score 受到相对距离影响很多，也就是由于Rope的存在使得注意力分数的远程衰减影响较大，可能就会导致正确答案的分数过低，找不到知识，模型表现不佳，因此越是要训练长context模型，Rope的theta就越是要设置的越大越好。
详见：(43 封私信 / 82 条消息) Rope 旋转位置编码 超参数theta的影响 - 知乎https://zhuanlan.zhihu.com/p/692197097
-
生成时间序列
t = torch.arange(end, device=freqs.device) 生成一个从0到end的序列，长度为end。
end通常是序列的最大长度。
序列中的每个元素都代表一个token。
-
计算频率的外积
freqs = torch.outer(t, freqs).float() 计算时间序列 t 和频率序列 freqs 的外积，得到一个二维矩阵 freqs。每一行是时间序列 t 的元素乘以频率序列 freqs 的元素。
-
计算实部和虚部
freqs_cos = torch.cos(freqs) 计算频率矩阵 freqs 的余弦值，得到旋转嵌入的实部。
freqs_sin = torch.sin(freqs) 计算频率矩阵 freqs 的正弦值，得到旋转嵌入的虚部。
构造好旋转嵌入的函数后，我们来构造调整张量形状的reshape_for_broadcast函数。这个函数的主要目的是调整 freqs_cis 的形状，使其在进行广播操作时与 x 的维度对齐，从而能够进行正确的张量运算。
因为模型采用了多头注意力网络，所以词向量维度数大小应该是每个头的维度大小。
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
# 获取x的维度数
ndim = x.ndim
# 断言，确保1在x的维度范围内
assert 0 <= 1 < ndim
# 断言，确保freqs_cis的形状与x的第二维和最后一维相同
# 即文本序列长度seq_len 和 词向量维度数head_dim
# 因为模型采用了多头注意力网络，所以词向量维度数大小应该是每个头的维度大小
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
# 构造一个新的形状，除了第二维和最后一维，其他维度都为1，这样做是为了能够将freqs_cis与x进行广播操作
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
# 将freqs_cis调整为新的形状，并返回
return freqs_cis.view(shape)最后，我们可以通过如下代码实现旋转嵌入：
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cos: torch.Tensor,
freqs_sin: torch.Tensor
) -> Tuple[torch.Tensor, torch.Tensor]:
# 将查询和键张量转换为浮点数，并重塑形状以分离实部和虚部
xq_r, xq_i = xq.float().reshape(xq.shape[:-1] + (-1, 2)).unbind(-1)
xk_r, xk_i = xk.float().reshape(xk.shape[:-1] + (-1, 2)).unbind(-1)
# xq.shape[:-1]: 取xq的形状中除了最后一个维度之外的所有维
# reshape(xq.shape[:-1] + (-1, 2)):
# (-1, 2)是一个新的维度形状
# 其中-1表示自动计算这个维度的大小，2表示最后一个维度的大小为2。
# reshape后：(batch_size, seq_len, n_head, head_dim)
# --> (batch_size, seq_len, n_head, head_dim/2, 2)
# 每一个dim//head最后两维度：[[q_0, q_1],
# [q_2, q_3],
# [q_4, q_5],
# ·········,
# [q_head_dim-2, q_head_dim-1]]
# .unbind(-1): 沿着张量的最后一个维度进行拆分
# 最后一个维度大小是2，则拆分成两个张量，分别为实部和虚部
# 每个张量为: (batch_size, seq_len, n_head, head_dim/2)
# 张量1: xq_r最后维度[q_0, 张量2: xq_i最后维度[q_1,
# q_2, q_3,
# q_4, q_5,
# ···, ···,
# q_head_dim-2] q_head_dim-1]
# 重新塑形频率张量以进行广播
# freqs_cos:(seq_len,
最低0.47元/天 解锁文章
扫一扫
630
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
