【LLM评价指标】从概率到直觉：理解语言模型的困惑度

“如果你想知道一个语言模型到底有多聪明，它在写下一个词时心里有多少个备选答案，就得看看困惑度了。”

​ 无论是 n-gram 语言模型（unigram、bigram、trigram）还是理论上可以记忆无限上下文的 递归神经网络语言模型（RNN LM），一个核心问题始终存在：如何评价语言模型的好坏？

​ 语言模型广泛应用于文本生成、语言预测等任务。最直接的评估方法是将其用于下游 NLP 任务中观察性能，但这种方法复杂且耗时。我们需要一个直接、量化的指标，来衡量语言模型本身的质量。

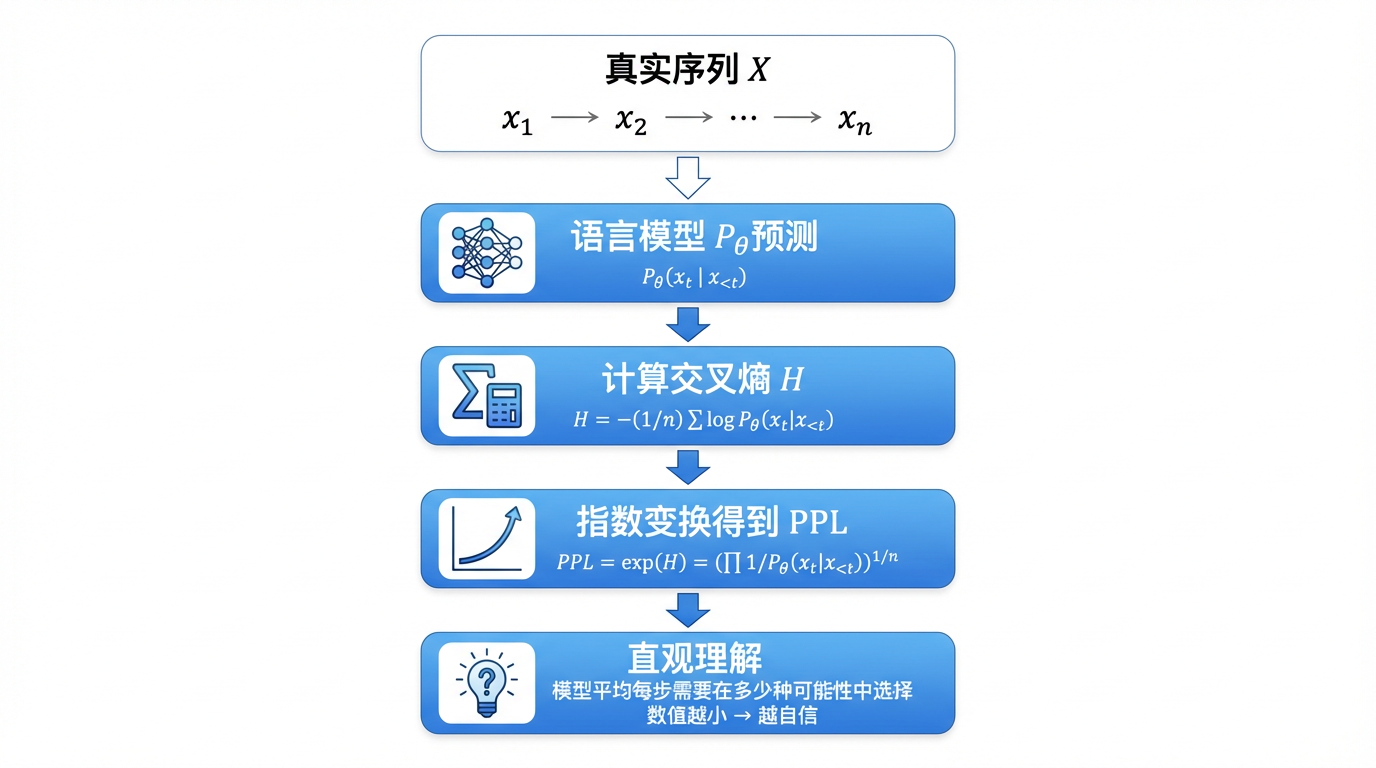
一、语言模型预测能力的直观理解

示例来自沐神教程：8.4.4 困惑度

​ 一个高质量的语言模型应当能够以较高的条件概率预测序列中下一个词元。以提示 “It is raining …” 为例，不同语言模型可能给出风格和质量差异极大的续写。

1. “It is raining outside”（外面下雨了）；

2. “It is raining banana tree”（香蕉树下雨了）；

3. “It is raining piouw;kcj pwepoiut”（piouw;kcj pwepoiut下雨了）。

​ 从语义连贯性和语言统计规律的角度看，这些续写反映了模型在不同层次上对真实语言分布的拟合程度。

• 就质量而言，例1显然是最合乎情理、在逻辑上最连贯的。 虽然这个模型可能没有很准确地反映出后续词的语义， 比如，“It is raining in San Francisco”（旧金山下雨了） 和``“It is raining in winter”（冬天下雨了）` 可能才是更完美的合理扩展， 但该模型已经能够捕捉到跟在后面的是哪类单词。

• 例2则要糟糕得多，因为其产生了一个无意义的续写。 尽管如此，至少该模型已经学会了如何拼写单词， 以及单词之间的某种程度的相关性。

• 例3表明了训练不足的模型是无法正确地拟合数据的。

  上述直观例子揭示了语言模型预测能力的差异，但仍然缺乏一个可比较、可量化的指标。

二、从序列似然到平均不确定性

​ 为了定量刻画模型对真实语言分布的拟合程度，我们可以考虑模型在给定真实序列上的似然概率。

​ 对于句子$\mathbf{X}=[x_1,x_2,\cdots ,x_n]$，其联合概率为：
$$P(\mathbf{X})=P(x_1,x_2,\cdots ,x_n)=P(x_1)P(x_2|x_1)\cdots P(x_n|x_1,\cdots ,x_{n-1})$$

• 直接比较完整序列的联合概率存在问题：
  • 序列越长，其联合概率天然越小：较短的序列比较长的序列更有可能出现
  • 不同样本长度不同，使得数值本身缺乏可比性。
• 因此，我们需要一种能够消除序列长度影响、刻画模型平均预测能力的度量方式。

三、交叉熵与平均不确定性

​ 信息论为这一问题提供了自然的解决方案。语言模型可以被理解为一个条件概率编码器：模型对真实词元的预测概率越高，就意味着在编码该序列时，所需的平均码长越短。

​ 形式上，语言模型定义了一个条件概率分布：
$$P_{\theta }(x_t|x_{<t})$$
​ 其中，$P_{\theta }(x_t|x_{<t})$表示模型在时间步$t$下，在给定历史上下文 $x_{<t}=(x_1,\dots ,x_{t-1})$ 的条件下，对词元 $x_t$ 的预测概率（或对数似然值）。

​ 从概率编码的角度看，一个更好的语言模型，应当能够在平均意义下更准确地预测真实出现的词元，从而降低文本的不确定性。

​ 在实践中，这种平均不确定性通常通过 token 级交叉熵 来衡量。给定长度为 $n$ 的序列$\mathbf{X}=[x_1,x_2,\dots ,x_n]$，其交叉熵定义为：
$$\begin{array}{rl}H& =\frac{1}{n}\sum _{t=1}^n-\log P(x_t|x_{t-1},\cdots ,x_1)\end{array}$$
​ 其中，$x_t$表示在时间步$t$观察到的真实词元，$H$刻画了模型在真实数据分布下的平均不确定性，由于取了平均值，它天然消除了序列长度带来的影响。

• 交叉熵越低 → 模型预测越准确 → 平均编码长度越短。

​ 至此，我们已经得到了一个能够衡量语言模型平均预测不确定性的指标。在工程实践中，人们通常对这一量再做一次指数变换，从而得到更直观的评价指标：困惑度（Perplexity）。

四、困惑度

perplexity

​ 由于历史和工程实践的原因，自然语言处理领域通常不直接使用交叉熵本身，而是采用其指数形式，即困惑度—个在数值尺度和直觉上都更易理解的指标。

1. 交叉熵的指数形式

​ 设有一个长度为$n$的分词序列$\mathbf{X}=[x_1,x_2,\dots ,x_n]$，基于交叉熵$H$的困惑度可以表示为：
$$\begin{array}{rl}\text{PPL}(\mathbf{X})& =\exp (H)\\ & =\exp (-\frac{1}{n}\sum _{t=1}^n\log P(x_t\mid x_1,\dots ,x_{t-1}))\\ & =\left[\exp \right(\sum _{t=1}^n\log P(x_t\mid x_{<t})){]}^{-\frac{1}{n}}\\ & =(\prod _{t=1}^{n}P(x_t\mid x_{<t}){)}^{-\frac{1}{n}}\\ & =\sqrt[n]{\prod _{t=1}^n\frac{1}{P(x_t\mid x_{<t})}}.\end{array}$$
​ 可以看到，根号内是整个句子概率的倒数，因此：句子在模型下的概率越大，困惑度越小，模型对该句子就越“不困惑”。

​ 此外，开$n$次方根（$n$为句子长度）意味着对 token 概率取几何平均，从而消除了序列长度对评价结果的影响，使得不同长度句子之间具有可比性。

​ 从这个角度看，困惑度可以理解为：模型在平均每一个时间步上，对下一个词元的不确定性大小。

​

2. 困惑度：序列负对数似然的指数平均值

​ 困惑度也常被直接定义为序列联合概率的负幂平均值。

​ 对同一序列$\mathbf{X}$：
$$\begin{array}{rl}\text{PPL}(\mathbf{X})& =[P(x_1,x_2,\cdots ,x_n){]}^{-\frac{1}{n}}\\ & =[P(x_1)P(x_2|x_1)\cdots P(x_n|x_1,\cdots ,x_{n-1}){]}^{-\frac{1}{n}}\\ & =\sqrt[n]{\frac{1}{{\prod }_{t=1}^{n}P(x_t|x_{<t})}}\end{array}$$

• 这种写法直接强调了困惑度与整个序列概率之间的关系：
  • 若模型对整句赋予较高的联合概率 → 困惑度较小
  • 若模型对序列整体“难以置信” → 困惑度较大

3. 两种视角的统一理解

• 交叉熵视角：
  困惑度是“平均每个 token 的不确定性”的指数形式

• 联合概率视角：
  困惑度是“序列整体概率的归一化逆量”

  二者在数学上完全等价，只是强调角度不同。

​ 因此，困惑度并不是一个新的概念，而是对平均不确定性的另一种表达方式，可以被理解为：模型在预测下一个词元时，平均需要在多少种可能性中做选择。

五、困惑度的直观理解

参考知乎文章示例：LLM评估指标困惑度的理解

​ 假设我们的测试文档只有一句话：

“爱你就像爱生命。”

​ 词表（token）只有 7 个：

tokens_map = {
    '爱': 0,
    '你': 1,
    '就': 2,
    '像': 3,
    '生': 4,
    '命': 5,
    '。': 6,
}

1. 模型输出概率矩阵

​ 使用 GPT 类模型生成句子时，通常会得到形状为 [句子长度, 词表长度] 的概率矩阵。对于我们当前的示例，句子长度 = 8（“爱 你 就 像 爱 生 命。” 一共 8 个词元），词表长度 = 7（词表 tokens_map 有 7 个 token）。

​ 所以矩阵就是 8 行 7 列，每一行对应一个词元的预测情况，每一列对应词表中的某个词。

​ 假设有两个模型 A 和 B，其预测概率如下：

# modelA
probs_modelA = [
    [0.16, 0.16, 0.16, 0.16, 0.16, 0.16, 0.04], 
    [0.05, 0.30, 0.05, 0.40, 0.05, 0.10, 0.05], 
    [0.30, 0.05, 0.30, 0.20, 0.05, 0.05, 0.05], 
    [0.20, 0.10, 0.05, 0.50, 0.05, 0.05, 0.05], 
    [0.30, 0.30, 0.05, 0.05, 0.10, 0.15, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.35, 0.30, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.05, 0.60, 0.05]，
    [0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.70]
]

# modelB
probs_modelB = [
    [0.16, 0.16, 0.16, 0.16, 0.16, 0.16, 0.04], 
    [0.05, 0.50, 0.05, 0.20, 0.05, 0.10, 0.05], 
    [0.30, 0.05, 0.40, 0.10, 0.05, 0.05, 0.05], 
    [0.10, 0.10, 0.05, 0.60, 0.05, 0.05, 0.05], 
    [0.40, 0.30, 0.05, 0.05, 0.10, 0.05, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.40, 0.25, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.05, 0.60, 0.05]，
    [0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.70]
]

​ 其中，第$t$行表示模型在当前时间步（生成第$t$个词元时），对词表中的每个词的预测概率。此外，注意第 2 个词元的概率分布是条件概率，依赖于前面生成的词。

2. 取句子中实际词元的概率

​ 计算句子概率序列（取每个时间步真实词元的预测概率）。

​ 下表列出了每个词元在模型预测下的概率，便于直观对比模型 A 和 B 的预测能力：

词元	A概率	B概率
爱	0.16	0.16
你	0.30	0.50
就	0.30	0.40
像	0.50	0.60
爱	0.30	0.40
生	0.35	0.40
命	0.60	0.60
。	0.70	0.70

第 1 个词元是 爱（token 0），对应 probs_modelA 的第 0 行第 0 列 → 0.16

第 2 个词元是 你（token 1），对应第 1 行第 1 列 → 0.30

第 3 个词元是 就（token 2），对应第 2 行第 2 列 → 0.30

​ 可以直观地看到，模型 B 对大部分词元的预测概率更高。

3. 计算句子联合概率

​ 模型生成整个句子的概率为各词元概率连乘：
$$P(\mathbf{X})=\prod _{t=1}^{n}P(x_t|x_{<t})$$
​ 为了避免数字过小，可以取 $\log$ 或${\log }_2$计算。

• 模型A：$P(\mathbf{X}{)}_A={\log }_2(0.16\times 0.30\times 0.30\times 0.50\times 0.30\times 0.35\times 0.60\times 0.70)=-11.62$

• 模型B：$P(\mathbf{X}{)}_B={\log }_2(0.16\times 0.50\times 0.40\times 0.60\times 0.40\times 0.40\times 0.60\times 0.70)=-9.59$

  可以看到$P(\mathbf{X})_A < P(\mathbf{X})_B $ ，这说明模型B生成这句话的概率更高。

​ 这个结果我们可以理解为模型B可能是一个作家，相对更容易写出这样的句子，模型A是一个刚入门的作者，很难写出这样的句子。所以在这个测试集下B比A好。

4. 计算困惑度

​ 根据困惑度公式：
$$\begin{array}{rl}\text{PPL}(\mathbf{X})& =\sqrt[n]{\frac{1}{{\prod }_{t=1}^{n}P(x_t|x_{<t})}}\end{array}$$

• 模型 A： $\text{PPL}(\mathbf{X}{)}_A\approx 3.28$

• 模型 B：$\text{PPL}(\mathbf{X}{)}_B\approx 2.56$

  数值越小 → 模型越自信、越不困惑 → 模型 B 优于模型 A

六、结语

​ 困惑度（Perplexity, PPL）衡量了语言模型在预测序列时的“心智状态”：数值越小，表示模型在每一步预测下一个词元时更自信、备选方案更少，也就是越不困惑。

​ 可以想象你在玩一个写句子的小游戏：每写一个词，你心里都有一堆备选单词。困惑度就是告诉你平均每一步有多少个备选词。