ELM：一个强大的时间序列算法（附数据源码）

文章较长，示例代码在第三个部分，如需要数据及源码，关注微信公众号【爱敲代码的破晓】，后台私信【20251222】

一、极限学习机（ELM）的基本原理

1.1 ELM的核心思想

极限学习机是一种单隐层前馈神经网络（SLFN） 的快速学习算法，由南洋理工大学黄广斌教授于2004年提出。其核心思想是：

• 随机初始化隐藏层参数：输入权重和偏置随机生成且固定不变

• 解析计算输出权重：通过求解线性方程组直接得到输出权重，无需迭代优化

• 极快的训练速度：相比传统神经网络，训练时间可减少几个数量级

1.2 ELM的数学模型

对于包含L个隐藏节点的单隐层前馈神经网络：

网络结构

• 输入层：n个节点

• 隐藏层：L个节点（激活函数g）

• 输出层：m个节点

数学表达式

给定N个训练样本{(xᵢ, tᵢ)}，其中xᵢ∈ℝⁿ，tᵢ∈ℝᵐ：

1. 隐藏层输出矩阵：

   H = g(W·X + B)

   其中：

   • W ∈ ℝ^(L×n)：输入权重（随机生成）

   • B ∈ ℝ^(L×1)：隐藏层偏置（随机生成）

   • X ∈ ℝ^(n×N)：输入矩阵

2. 输出层：

   Y = H·β

   其中β ∈ ℝ^(L×m)是输出权重

3. 目标函数：

   min ||Hβ - T||²

   其中T ∈ ℝ^(N×m)是目标矩阵

1.3 ELM的学习算法

ELM的学习过程分为三个步骤：# 伪代码说明ELM训练过程

def train_elm(X_train, y_train, n_hidden):
    # 1. 随机初始化输入层参数
    W = random_matrix(n_input, n_hidden)
    b = random_vector(n_hidden)

    # 2. 计算隐藏层输出矩阵H
    H = activation_function(dot(X_train, W) + b)

    # 3. 解析计算输出权重β（通过Moore-Penrose伪逆）
    # H·β = Y → β = H⁺·Y
    H_pinv = pinv(H)  # 伪逆计算
    beta = dot(H_pinv, y_train)

    return W, b, beta

1.4 ELM的数学优化原理

ELM的核心数学原理是通过最小二乘法直接求解输出权重：

β = HᵀT

其中H⁺是隐藏层输出矩阵H的Moore-Penrose广义逆，可通过以下方式计算：

1. 当H为列满秩时：β = (HᵀH)⁻¹HᵀT

2. 当H为行满秩时：β = Hᵀ(HHᵀ)⁻¹T

3. 一般情况：使用奇异值分解(SVD)计算伪逆

二、ELM与传统神经网络的对比

特性	ELM	传统神经网络（BP）
参数优化	仅优化输出层权重	优化所有权重
训练速度	极快（一次计算）	慢（迭代优化）
局部最优	避免局部最优	可能陷入局部最优
过拟合风险	较低	较高（需正则化）
泛化能力	良好	依赖于参数调整

三、ELM在时间序列预测中的优势

3.1 与传统时间序列方法的比较

3.1.1 ARIMA/SARIMA模型

• 原理：基于线性假设，使用自回归、差分和移动平均

• ELM优势：

  • 能捕捉非线性关系

  • 无需复杂的平稳性检验

  • 处理多变量交互更灵活

3.1.2 指数平滑法

• 原理：加权平均历史数据，近期数据权重更高

• ELM优势：

  • 能学习复杂模式，不仅仅是趋势和季节性

  • 更好地处理突变点和异常值

3.2 与其他机器学习方法的比较

3.2.1 支持向量机（SVR）

• SVR特点：基于结构风险最小化，寻找最优超平面

• ELM优势：

  • 训练速度更快：SVR需求解二次规划问题

  • 更容易调整：ELM主要调整隐藏层节点数

  • 更适合大规模数据

3.2.2 传统BP神经网络

• BP特点：反向传播，梯度下降优化

• ELM优势：

  • 避免梯度消失/爆炸问题

  • 训练速度极快（数十到数百倍加速）

  • 无需学习率调整

3.2.3 深度学习模型（LSTM/GRU）

• 深度学习特点：多层结构，强大的特征提取能力

• ELM优势：

  • 计算资源需求低

  • 训练速度极快

  • 小数据表现更好

  • 超参数调优简单

3.3 ELM的独特优势总结

优势维度	具体表现
计算效率	训练速度比传统神经网络快10-1000倍
实现简单	无需复杂调参，主要调整隐藏节点数
全局最优	解析解确保找到全局最优输出权重
泛化性能	理论证明具有良好的泛化能力
数值稳定	避免梯度消失/爆炸问题

四、ELM在时间序列预测中的应用特点

4.1 数据处理特点python

# ELM处理时间序列的典型方式
def prepare_time_series_elm(data, look_back):
    """
    将时间序列转换为监督学习问题
    使用滑动窗口方法
    """
    X, y = [], []
    for i in range(len(data) - look_back):
        # 输入：过去look_back个时间点的数据
        X.append(data[i:i+look_back])
        # 输出：下一个时间点的数据
        y.append(data[i+look_back])
    return np.array(X), np.array(y)

# ELM的优势：能直接处理这种固定窗口的转换
# 而RNN/LSTM可以处理变长序列，但训练更复杂

4.2 参数敏感性分析

ELM的主要超参数是隐藏层节点数(L)，其选择策略：

1. 经验公式：L = 2n ~ 10n（n为输入维度）

2. 实验选择：通过交叉验证确定最优L

3. 自适应方法：逐步增加节点直到性能不再提升

五、ELM与其他算法的性能对比研究

5.1 实验研究结果汇总

根据多项研究论文的比较结果：

算法	训练时间	预测精度	参数敏感性	适用场景
ELM	★★★★★	★★★★☆	★★★☆☆	快速原型、实时预测
LSTM	★★☆☆☆	★★★★★	★☆☆☆☆	复杂序列、长期依赖
SVR	★★★☆☆	★★★☆☆	★★☆☆☆	小样本、线性可分
ARIMA	★★★★☆	★★☆☆☆	★★★★☆	线性、平稳序列
Prophet	★★★★☆	★★★☆☆	★★★☆☆	商业时间序列

5.2 各算法的时间复杂度比较

 算法               训练复杂度        预测复杂度      适用数据规模
 ELM               O(N·L²)               O(L·m)            大/中/小
 BP神经网络    O(N·epoch·L²)    O(L·m)            小/中
 LSTM             O(N·epoch·L³)    O(L·m)            小/中
 SVR               O(N² ~ N³)         O(SV)              小
 随机森林       O(N·√p·T)            O(T·深度)         大/中

注：N-样本数，L-隐藏节点数，epoch-迭代次数，p-特征数，T-树的数量

六、应用方向

6.1 ELM的研究方向

1. 理论深化：泛化误差界、最优隐藏节点数理论

2. 结构创新：图ELM、注意力ELM、Transformer+ELM

3. 应用扩展：时空预测、多任务学习、迁移学习

4. 效率优化：分布式ELM、量子ELM、硬件加速

6.2 ELM在时间序列领域的潜力

随着边缘计算和物联网的发展，ELM因其高效性在以下领域有巨大潜力：

1. 实时工业预测：设备故障预警、质量监控

2. 金融高频交易：毫秒级价格预测

3. 智慧城市：交通流量、能耗实时预测

4. 健康医疗：可穿戴设备的实时生理信号分析

七、应用实例

7.1.数据准备

以下面股票数据为例，并来开盘价Open为目标函数

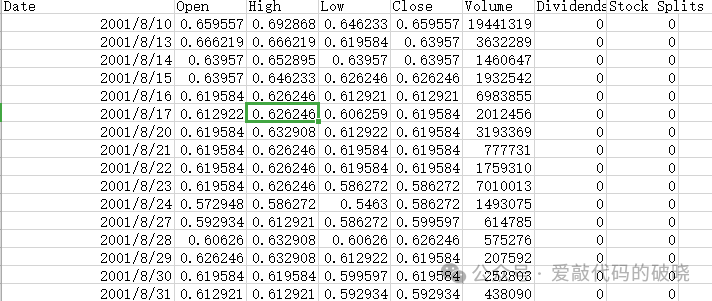
7.2.导入库

导入第三方库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import joblib
import os
import sys
import warnings
from scipy.linalg import pinv2
from datetime import datetime
import argparse

warnings.filterwarnings('ignore')

7.3.设置中文

# 设置中文字体（如果系统支持）
try:
    plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
    plt.rcParams['axes.unicode_minus'] = False
except:

7.4训练模型

def main_train(file_path, look_back=15, n_hidden=100, activation='sigmoid', 
               random_state=42, test_size=0.2, save_dir='saved_models'):
    """
    训练模型的主函数

    参数:
    - file_path: 数据文件路径
    - look_back: 时间窗口大小
    - n_hidden: 隐藏层神经元数量
    - activation: 激活函数
    - random_state: 随机种子
    - test_size: 测试集比例
    - save_dir: 保存目录
    """
    print("="*70)
    print("开始训练极限学习机(ELM)时间序列预测模型")
    print("="*70)

    # 1. 初始化时间序列ELM模型
    ts_elm = TimeSeriesELM(
        look_back=look_back,
        n_hidden=n_hidden,
        activation=activation,
        random_state=random_state,
        test_size=test_size
    )

    # 2. 加载和预处理数据
    try:
        (df, dates, X_train, X_test, y_train, y_test, 
         train_dates, test_dates) = ts_elm.load_and_preprocess(file_path)
    except Exception as e:
        print(f"数据加载失败: {e}")
        return None

    # 3. 训练模型
    y_train_orig, y_train_pred = ts_elm.train(X_train, y_train)

    # 4. 评估训练集
    train_metrics = ts_elm.evaluate(y_train_orig, y_train_pred, "训练集")

    # 5. 在测试集上预测
    print("\n在测试集上进行预测...")
    _, y_test_pred = ts_elm.predict(X_test)
    y_test_orig = ts_elm.inverse_transform(y_test).ravel()

    # 6. 评估测试集
    test_metrics = ts_elm.evaluate(y_test_orig, y_test_pred, "测试集")

    # 7. 保存模型
    ts_elm.save_model(save_dir)

    # 8. 绘制测试集预测结果
    ts_elm.plot_predictions(
        y_test_orig, y_test_pred, test_dates,
        title=f"测试集预测结果 (R²={test_metrics['R2']:.4f})",
        save_path=os.path.join(save_dir, 'test_predictions.png')
    )

    # 9. 绘制综合评估图表
    ts_elm.plot_comprehensive_evaluation(
        y_test_orig, y_test_pred, test_dates,
        save_dir=save_dir
    )

    # 10. 打印详细预测结果
    ts_elm.print_prediction_details(y_test_orig, y_test_pred, test_dates)

    # 11. 保存评估指标到CSV
    metrics_df = pd.DataFrame({
        '数据集': ['训练集', '测试集'],
        'MAPE': [train_metrics['MAPE'], test_metrics['MAPE']],
        'MAE': [train_metrics['MAE'], test_metrics['MAE']],
        'MSE': [train_metrics['MSE'], test_metrics['MSE']],
        'RMSE': [train_metrics['RMSE'], test_metrics['RMSE']],
        'R2': [train_metrics['R2'], test_metrics['R2']]
    })

    metrics_path = os.path.join(save_dir, 'evaluation_metrics.csv')
    metrics_df.to_csv(metrics_path, index=False)
    print(f"\n评估指标已保存到: {metrics_path}")

    print("\n" + "="*70)
    print("模型训练和评估完成!")
    print("="*70)

    return ts_elm, train_metrics, test_metrics

7.5模型预测

def main_predict(file_path, model_dir='saved_models', n_predictions=20):
    """
    使用已训练模型进行预测的主函数

    参数:
    - file_path: 数据文件路径
    - model_dir: 模型保存目录
    - n_predictions: 要生成的预测数量
    """
    print("="*70)
    print("使用已训练的ELM模型进行预测")
    print("="*70)

    # 1. 初始化时间序列ELM模型
    ts_elm = TimeSeriesELM()

    # 2. 加载已训练的模型
    try:
        ts_elm.load_model(model_dir)
        print("模型加载成功!")
    except Exception as e:
        print(f"模型加载失败: {e}")
        return None

    # 3. 加载和预处理数据
    try:
        (df, dates, X_train, X_test, y_train, y_test, 
         train_dates, test_dates) = ts_elm.load_and_preprocess(file_path)
    except Exception as e:
        print(f"数据加载失败: {e}")
        return None

    # 4. 在测试集上预测
    _, y_test_pred = ts_elm.predict(X_test)
    y_test_orig = ts_elm.inverse_transform(y_test).ravel()

    # 5. 评估测试集
    test_metrics = ts_elm.evaluate(y_test_orig, y_test_pred, "测试集")

    # 6. 绘制测试集预测结果
    ts_elm.plot_predictions(
        y_test_orig, y_test_pred, test_dates,
        title=f"测试集预测结果 (R²={test_metrics['R2']:.4f})",
        save_path=os.path.join(model_dir, 'test_predictions_new.png')
    )

    # 7. 绘制综合评估图表
    ts_elm.plot_comprehensive_evaluation(
        y_test_orig, y_test_pred, test_dates,
        save_dir=model_dir
    )

    # 8. 打印详细预测结果
    ts_elm.print_prediction_details(y_test_orig, y_test_pred, test_dates)

    # 9. 生成未来预测（如果数据足够）
    if len(X_test) > 0:
        print("\n生成未来预测...")
        # 使用最后look_back个数据点进行预测
        last_sequence = X_test[-1].reshape(1, -1)

        future_predictions = []
        future_dates = []

        # 生成未来预测
        for i in range(min(n_predictions, 30)):  # 最多预测30天
            # 预测下一天
            _, next_pred = ts_elm.predict(last_sequence)
            future_predictions.append(next_pred[0])

            # 生成未来日期
            last_date = test_dates[-1]
            if isinstance(last_date, np.datetime64) or hasattr(last_date, 'strftime'):
                try:
                    future_date = pd.Timestamp(last_date) + pd.Timedelta(days=i+1)
                except:
                    future_date = f"Day {i+1}"
            else:
                future_date = f"Day {i+1}"

            future_dates.append(future_date)

            # 更新序列用于下一次预测
            last_sequence = np.roll(last_sequence, -1)
            last_sequence[0, -1] = next_pred[0] / ts_elm.scaler.data_range_[0] + ts_elm.scaler.data_min_[0]

        # 绘制未来预测
        plt.figure(figsize=(12, 6))
        plt.plot(test_dates[-30:], y_test_orig[-30:], 'b-', label='历史实际值', linewidth=2)
        plt.plot(future_dates, future_predictions, 'r--', label='未来预测', linewidth=2, marker='o')
        plt.title('未来预测结果', fontsize=16, fontweight='bold')
        plt.xlabel('日期', fontsize=12)
        plt.ylabel('开盘价 (Open)', fontsize=12)
        plt.legend(fontsize=12)
        plt.grid(True, alpha=0.3)
        plt.xticks(rotation=45)
        plt.tight_layout()

        future_plot_path = os.path.join(model_dir, 'future_predictions.png')
        plt.savefig(future_plot_path, dpi=300, bbox_inches='tight')
        print(f"未来预测图表已保存到: {future_plot_path}")
        plt.show()

        # 打印未来预测结果
        print(f"\n{'='*60}")
        print("未来预测结果")
        print(f"{'='*60}")
        print(f"{'日期':<15} {'预测值':<12}")
        print("-" * 30)
        for i in range(len(future_dates)):
            date_str = str(future_dates[i]) if not hasattr(future_dates[i], 'strftime') else future_dates[i].strftime('%Y-%m-%d')
            print(f"{date_str:<15} {future_predictions[i]:<12.4f}")

    print("\n" + "="*70)
    print("预测完成!")
    print("="*70)

    return ts_elm, test_metrics

导出以下图件

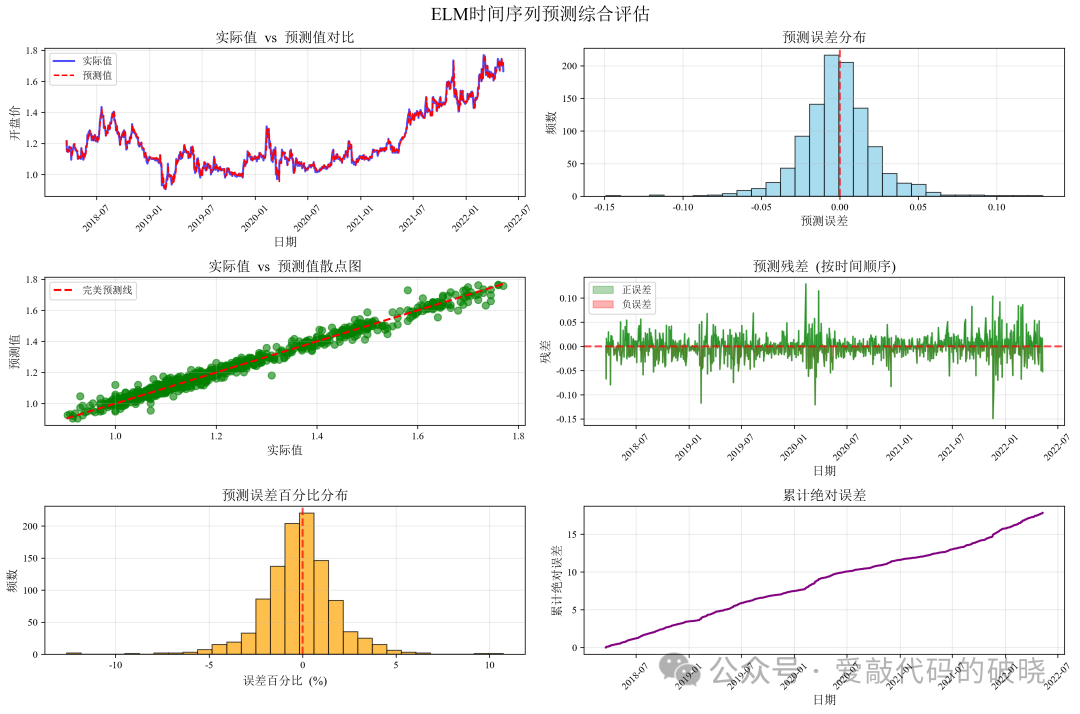
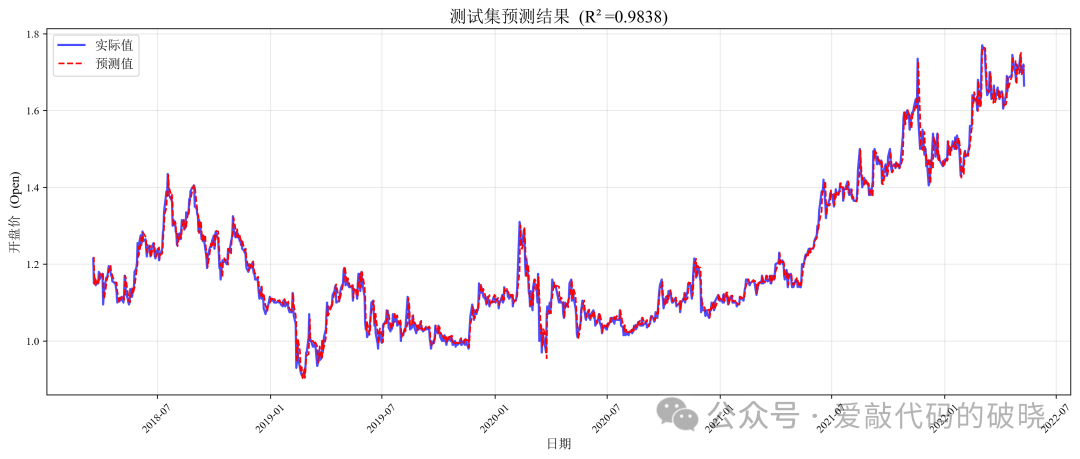
以下是参数评估

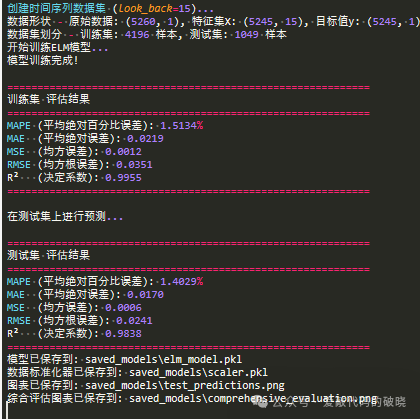
7.5模型预测

代码的使用方法:

使用方法1
# 训练模型
python elm_ts_prediction.py train --data AAC.AX.csv

# 使用已训练模型进行预测
python elm_ts_prediction.py predict --data AAC.AX.csv

# 完整流程：训练并预测
python elm_ts_prediction.py full --data AAC.AX.csv

# 自定义参数训练
python elm_ts_prediction.py train --data AAC.AX.csv --look_back 20 --hidden 150 --test_size 0.15

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
使用方法2
# 首先，修改train.py和predict.py中的文件路径
# 然后运行：

# 训练模型
python train2.py

# 使用已训练模型进行预测
python predict2.py

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
使用方法3
# 在Python中直接使用
from elm_ts_prediction import TimeSeriesELM, main_train, main_predict

# 训练模型
ts_elm, train_metrics, test_metrics = main_train(
    file_path="AAC.AX.csv",
    look_back=15,
    n_hidden=100,
    activation="sigmoid",
    random_state=42,
    test_size=0.2,
    save_dir="saved_models"
)

# 或使用已训练模型进行预测
ts_elm, test_metrics = main_predict(
    file_path="AAC.AX.csv",
    model_dir="saved_models",
    n_predictions=10
)

八、总结

极限学习机作为一种高效、简单、性能良好的时间序列预测方法，在以下方面具有显著优势：

1. 速度优势：训练速度远超传统迭代算法

2. 实现简便：无需复杂调参，易于部署

3. 理论保证：具有数学上的最优性保证

4. 适用广泛：适用于多种时间序列类型

然而，ELM并非万能解决方案，其随机初始化的特点可能导致结果不稳定，且对长期依赖关系的建模能力有限。在实际应用中，建议：

• 对稳定性要求高的场景使用集成ELM

• 对精度要求极高的场景考虑混合模型（ELM+其他方法）

• 对实时性要求严的场景优先选择ELM

ELM代表了机器学习中效率与性能平衡的一个重要方向，特别适合当今大数据和实时分析的需求，是时间序列预测工具箱中一个值得掌握的重要工具。

如需要数据及源码，关注微信公众号【爱敲代码的破晓】，后台私信【20251222】