文章较长,示例代码在第三个部分,如需要数据及源码,关注微信公众号【爱敲代码的破晓】,后台私信【20251229】
一、GMM聚类算法基本原理
1. 核心思想:混合分布模型
GMM的核心思想是假设所有数据点是由多个不同的高斯分布(正态分布)混合生成的。想象一下,你的数据不是单一来源,而是来自几个不同的"工厂",每个"工厂"生产数据的方式略有不同,但都遵循高斯分布的规律。这些"工厂"就是GMM中的高斯分量。
2. 概率建模:软分配机制
GMM采用概率方法进行聚类。与"非黑即白"的硬分配不同,GMM认为每个数据点都可能属于任何一个聚类,只是概率大小不同。比如,一个数据点可能属于聚类A的概率是70%,属于聚类B的概率是25%,属于聚类C的概率是5%。这种软分配让聚类结果更加细腻和合理。
3. 数据生成过程
你可以这样理解GMM的数据生成过程:
-
第一步:随机选择一个高斯分量(类似抽签,每个分量被选中的概率不同)
-
第二步:从选中的高斯分量中随机生成一个数据点
-
第三步:重复以上过程,生成整个数据集
这个生成过程的逆过程就是聚类——给定数据,我们推断最可能是哪些高斯分量生成了它们。
4. EM算法:两步迭代优化
GMM使用期望最大化(EM)算法来学习模型参数,这个过程就像两个角色交替工作:
角色一:分配者(E步)
分配者的任务是:基于当前对高斯分量的理解(位置、形状、大小),计算每个数据点"应该"属于哪个分量。但它不做硬性决定,而是给出一个"责任分配表"——每个点对每个分量的归属概率。
角色二:调整者(M步)
调整者的任务是:根据分配者提供的责任分配表,重新调整高斯分量的参数:
-
调整位置:如果某些点以较高概率属于某个分量,就把这个分量向这些点移动
-
调整形状:根据点的分布情况,调整分量的形状(是圆形的还是椭圆形的)
-
调整大小:根据归属于每个分量的点的总概率,调整分量的大小和重要性
迭代过程:
两个角色反复协作,分配者根据调整者更新后的分量重新计算概率,调整者再根据新的概率重新调整分量。这个过程反复进行,直到高斯分量的参数基本不再变化。
5. 聚类形成
当EM算法收敛后,每个高斯分量就定义了一个聚类:
-
分量的中心定义了聚类的中心位置
-
分量的形状定义了聚类的区域形状
-
分量的大小和权重定义了聚类的重要性
最终,每个数据点被分配到它归属概率最高的那个高斯分量所对应的聚类。
6. 协方差的灵活性
GMM允许每个高斯分量有不同的"形状"设置:
-
完全灵活型:每个分量可以有自己的任意椭圆形状和方向
-
相同形状型:所有分量必须是同样的形状和方向
-
轴对齐型:每个分量的椭圆必须与坐标轴对齐
-
球形型:每个分量必须是圆形
这种灵活性让GMM能够适应各种复杂的数据分布。
7. 不确定性量化
GMM的一个重要特点是能够量化聚类的不确定性:
-
对于远离所有分量中心的点,其归属概率分布会相对均匀,表明"不确定它属于哪一类"
-
对于靠近分量中心的点,其归属概率会高度集中在某个分量上,表明"很有信心地分类"
-
这种不确定性信息在很多实际应用中非常有用
8. 模型选择与聚类数确定
GMM不需要预先精确指定聚类数,可以通过信息准则(AIC/BIC)来选择:
-
AIC准则:倾向于选择更复杂的模型(更多的聚类数)
-
BIC准则:倾向于选择更简单的模型(更少的聚类数)
-
通过比较不同聚类数下的这些准则值,可以选择最合适的聚类数
二、GMM与其他聚类算法的差异本质
1. 与K-means的本质区别
K-means的世界观:世界是由清晰的边界划分的,每个点只能属于一个区域,区域之间互不重叠。它像用圆规画圆一样划分空间。
GMM的世界观:世界是模糊的、概率性的,边界是渐变的。它认为数据点可能同时具有多个聚类的特性,只是程度不同。GMM更像是在描述一种"渐变"的归属关系。
2. 与DBSCAN的本质区别
DBSCAN的世界观:关注数据的"密度",认为聚类是高密度区域,低密度区域是噪声或边界。
GMM的世界观:关注数据的"统计分布",假设数据来自多个统计分布,每个分布对应一个聚类。GMM试图找到这些分布的参数。
3. 与层次聚类的本质区别
层次聚类的世界观:关注数据点之间的"相对距离关系",通过逐步合并或分裂来构建聚类层次结构。
GMM的世界观:关注数据的"整体生成机制",假设数据是由特定统计过程生成的,并试图反推这个过程。
三、GMM聚类算法的实际应用
1. 导入第三方库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
from sklearn.metrics import adjusted_rand_score, normalized_mutual_info_score, confusion_matrix, classification_report
import warnings
warnings.filterwarnings('ignore')
2.绘图设置
# 设置中文字体和图形样式plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False# sns.set(style="whitegrid")
3.加载数据
# 1. 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征数据
y_true = iris.target # 真实标签
feature_names = iris.feature_names # 特征名称
target_names = iris.target_names # 类别名称
print("=" * 60)
print("鸢尾花数据集信息:")
print(f"特征形状: {X.shape}")
print(f"特征名称: {feature_names}")
print(f"类别名称: {target_names}")
print(f"类别分布: {np.bincount(y_true)}")
4.数据标准化
# 2. 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print("\n数据已标准化处理")
5.构造GMM框架并训练
# 3. 使用GMM进行聚类
# 由于我们知道鸢尾花有3个类别,设置n_components=3
gmm = GaussianMixture(
n_components=3, # 聚类数量
covariance_type='full', # 协方差类型:full, tied, diag, spherical
random_state=42,
init_params='kmeans', # 初始化方法:kmeans或random
max_iter=200,
tol=1e-3
)
# 训练模型并预测
# 获取每个样本属于每个聚类的概率
probabilities = gmm.predict_proba(X_scaled)
print("\nGMM模型参数:")
print(f"收敛迭代次数: {gmm.n_iter_}")
print(f"模型收敛: {gmm.converged_}")
print(f"对数似然值: {gmm.lower_bound_:.4f}")
print(f"AIC: {gmm.aic(X_scaled):.4f}")
print(f"BIC: {gmm.bic(X_scaled):.4f}")
6.结果评估
# 4. 评估聚类结果
print("\n" + "=" * 60)
print("聚类评估指标:")
# 内部评估指标(不需要真实标签)
silhouette = silhouette_score(X_scaled, y_pred)
davies_bouldin = davies_bouldin_score(X_scaled, y_pred)
print(f"轮廓系数 (Silhouette Score): {silhouette:.4f}")
print(f"Calinski-Harabasz指数: {calinski_harabasz:.4f}")
print(f"Davies-Bouldin指数: {davies_bouldin:.4f}")
# 外部评估指标(与真实标签比较)
ari = adjusted_rand_score(y_true, y_pred)
nmi = normalized_mutual_info_score(y_true, y_pred)
print("\n与真实标签对比的评估指标:")
print(f"调整兰德指数 (ARI): {ari:.4f}")
print(f"标准化互信息 (NMI): {nmi:.4f}")
7.对比分析
# 5. 创建对比分析
print("\n" + "=" * 60)
print("聚类结果与真实标签对比:")
# 统计每个聚类中的真实类别分布
comparison_df = pd.DataFrame({
'真实标签': y_true,
'聚类标签': y_pred
})
# 创建交叉表显示聚类结果与真实标签的关系
cross_tab = pd.crosstab(
comparison_df['聚类标签'],
comparison_df['真实标签'],
rownames=['聚类标签'],
colnames=['真实标签']
)
print("\n聚类标签 vs 真实标签交叉表:")
print(cross_tab)
# 计算每个聚类的纯度
for cluster in range(3):
cluster_indices = np.where(y_pred == cluster)[0]
if len(cluster_indices) > 0:
true_labels_in_cluster = y_true[cluster_indices]
most_common = np.bincount(true_labels_in_cluster).argmax()
purity = np.sum(true_labels_in_cluster == most_common) / len(true_labels_in_cluster)
purity_scores.append(purity)
print(f"聚类 {cluster} 的纯度: {purity:.4f} (主要类别: {target_names[most_common]})")
print(f"\n平均纯度: {np.mean(purity_scores):.4f}")
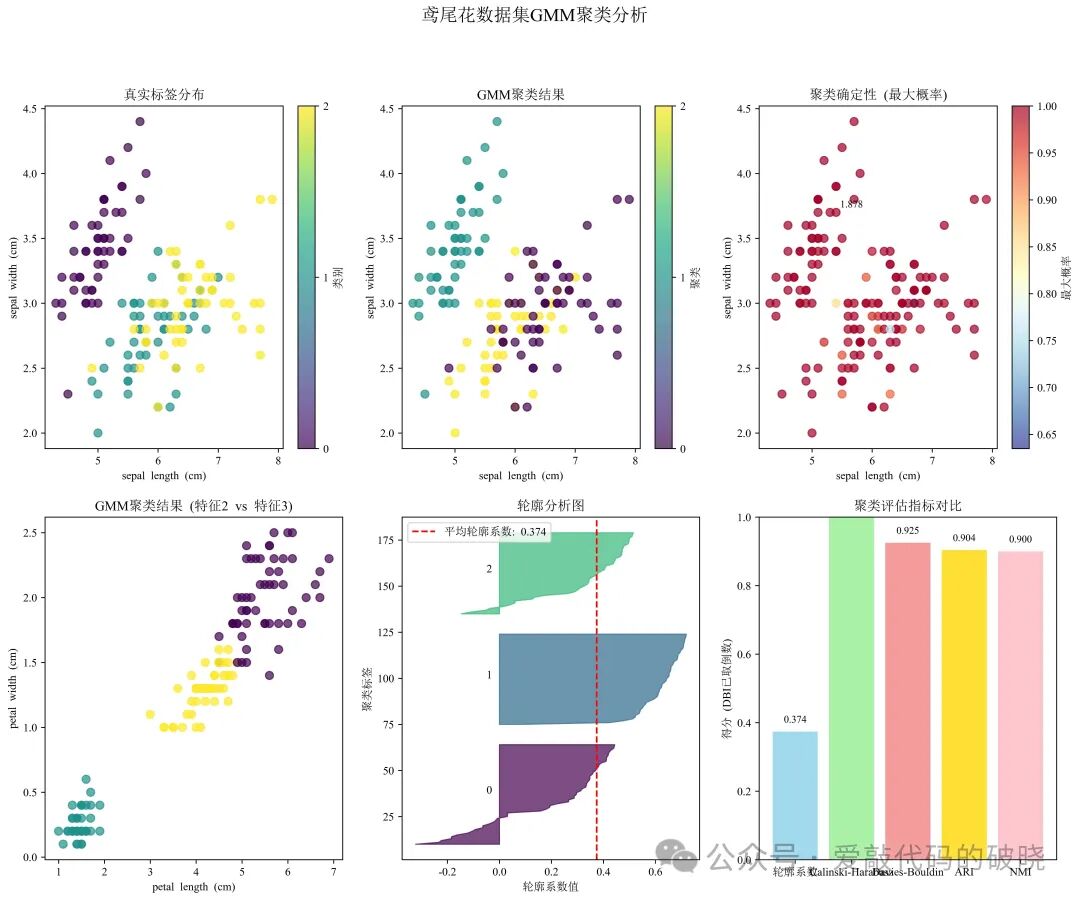
8.可视化
# 6. 可视化结果
fig = plt.figure(figsize=(16, 12))
# 6.1 真实标签可视化(前两个特征)
ax1 = plt.subplot(2, 3, 1)
scatter1 = ax1.scatter(X[:, 0], X[:, 1], c=y_true, cmap='viridis', s=50, alpha=0.7)
ax1.set_xlabel(feature_names[0])
ax1.set_ylabel(feature_names[1])
ax1.set_title('真实标签分布')
plt.colorbar(scatter1, ax=ax1, ticks=[0, 1, 2], label='类别')
# 6.2 聚类结果可视化(前两个特征)
ax2 = plt.subplot(2, 3, 2)
scatter2 = ax2.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=50, alpha=0.7)
ax2.set_xlabel(feature_names[0])
ax2.set_ylabel(feature_names[1])
ax2.set_title('GMM聚类结果')
plt.colorbar(scatter2, ax=ax2, ticks=[0, 1, 2], label='聚类')
# 6.3 聚类不确定性可视化(样本属于各聚类的最大概率)
ax3 = plt.subplot(2, 3, 3)
scatter3 = ax3.scatter(X[:, 0], X[:, 1], c=max_probs, cmap='RdYlBu_r', s=50, alpha=0.7)
ax3.set_xlabel(feature_names[0])
ax3.set_ylabel(feature_names[1])
ax3.set_title('聚类确定性 (最大概率)')
plt.colorbar(scatter3, ax=ax3, label='最大概率')
# 6.4 使用不同特征对的聚类结果
ax4 = plt.subplot(2, 3, 4)
scatter4 = ax4.scatter(X[:, 2], X[:, 3], c=y_pred, cmap='viridis', s=50, alpha=0.7)
ax4.set_xlabel(feature_names[2])
ax4.set_ylabel(feature_names[3])
ax4.set_title('GMM聚类结果 (特征2 vs 特征3)')
# 6.5 轮廓系数可视化
from sklearn.metrics import silhouette_samples
ax5 = plt.subplot(2, 3, 5)
silhouette_vals = silhouette_samples(X_scaled, y_pred)
y_lower = 10
for i in range(3):
cluster_silhouette_vals = silhouette_vals[y_pred == i]
cluster_silhouette_vals.sort()
size_cluster_i = cluster_silhouette_vals.shape[0]
y_upper = y_lower + size_cluster_i
color = plt.cm.viridis(float(i) / 3)
ax5.fill_betweenx(np.arange(y_lower, y_upper),
0, cluster_silhouette_vals,
facecolor=color, edgecolor=color, alpha=0.7)
ax5.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
ax5.axvline(x=silhouette, color="red", linestyle="--", label=f'平均轮廓系数: {silhouette:.3f}')
ax5.set_xlabel("轮廓系数值")
ax5.set_ylabel("聚类标签")
ax5.set_title("轮廓分析图")
ax5.legend()
# 6.6 评估指标对比图
ax6 = plt.subplot(2, 3, 6)
metrics = ['轮廓系数', 'Calinski-Harabasz', 'Davies-Bouldin', 'ARI', 'NMI']
values = [silhouette, calinski_harabasz/100, 1/davies_bouldin, ari, nmi] # 对DBI取倒数,值越大越好
colors = ['skyblue', 'lightgreen', 'lightcoral', 'gold', 'lightpink']
bars = ax6.bar(metrics, values, color=colors, alpha=0.8)
ax6.set_title('聚类评估指标对比')
ax6.set_ylabel('得分 (DBI已取倒数)')
ax6.set_ylim(0, 1)
# 在柱状图上添加数值标签
for bar, value in zip(bars, values):
height = bar.get_height()
ax6.text(bar.get_x() + bar.get_width()/2., height + 0.02,
f'{value:.3f}', ha='center', va='bottom', fontsize=9)
plt.suptitle('鸢尾花数据集GMM聚类分析', fontsize=16, fontweight='bold')
# plt.tight_layout()
plt.savefig("鸢尾花数据集GMM聚类分析.jpg", dpi = 600, bbox_inches = "tight")
plt.show()
# 7. 尝试不同的协方差类型
print("\n" + "=" * 60)
print("不同协方差类型的GMM模型比较:")
covariance_types = ['full', 'tied', 'diag', 'spherical']
results = []
for cov_type in covariance_types:
gmm_test = GaussianMixture(
n_components=3,
covariance_type=cov_type,
random_state=42
)
y_pred_test = gmm_test.fit_predict(X_scaled)
# 计算评估指标
ari_test = adjusted_rand_score(y_true, y_pred_test)
silhouette_test = silhouette_score(X_scaled, y_pred_test)
bic_test = gmm_test.bic(X_scaled)
results.append({
'协方差类型': cov_type,
'ARI': ari_test,
'轮廓系数': silhouette_test,
'BIC': bic_test,
'收敛迭代': gmm_test.n_iter_
})
results_df = pd.DataFrame(results)
print(results_df.to_string(index=False))
# 8. 寻找最佳聚类数(使用肘部法则和信息准则)
print("\n" + "=" * 60)
print("不同聚类数的模型比较:")
n_components_range = range(1, 10)
aic_scores = []
bic_scores = []
silhouette_scores = []
for n in n_components_range:
gmm_n = GaussianMixture(
n_components=n,
covariance_type='full',
random_state=42
)
gmm_n.fit(X_scaled)
y_pred_n = gmm_n.predict(X_scaled)
aic_scores.append(gmm_n.aic(X_scaled))
bic_scores.append(gmm_n.bic(X_scaled))
if n > 1: # 轮廓系数需要至少2个聚类
silhouette_scores.append(silhouette_score(X_scaled, y_pred_n))
else:
silhouette_scores.append(0)
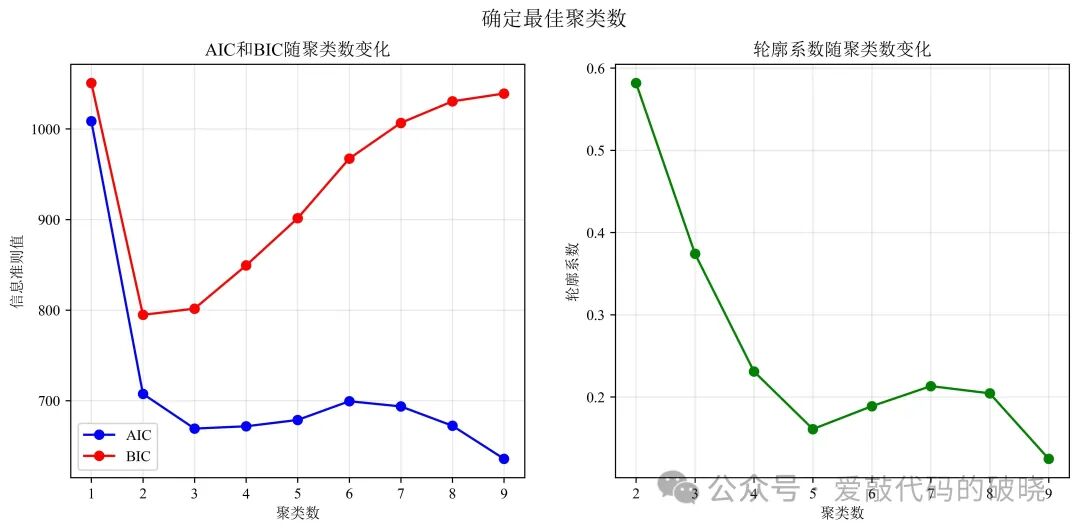
# 绘制信息准则图
fig2, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# AIC和BIC图
ax1.plot(n_components_range, aic_scores, 'bo-', label='AIC')
ax1.set_xlabel('聚类数')
ax1.set_ylabel('信息准则值')
ax1.set_title('AIC和BIC随聚类数变化')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 轮廓系数图
ax2.plot(n_components_range[1:], silhouette_scores[1:], 'go-')
ax2.set_xlabel('聚类数')
ax2.set_ylabel('轮廓系数')
ax2.set_title('轮廓系数随聚类数变化')
ax2.grid(True, alpha=0.3)
plt.suptitle('确定最佳聚类数', fontsize=14, fontweight='bold')
# plt.tight_layout()
plt.savefig("确定最佳聚类数.jpg", dpi = 600, bbox_inches = "tight")
plt.show()
# 输出最佳聚类数建议
optimal_n_aic = n_components_range[np.argmin(aic_scores)]
optimal_n_bic = n_components_range[np.argmin(bic_scores)]
optimal_n_silhouette = n_components_range[1:][np.argmax(silhouette_scores[1:])]
print(f"\n根据信息准则建议的最佳聚类数:")
print(f"AIC建议的聚类数: {optimal_n_aic}")
print(f"BIC建议的聚类数: {optimal_n_bic}")
print(f"轮廓系数建议的聚类数: {optimal_n_silhouette}")
# 9. 最终总结
print("\n" + "=" * 60)
print("分析总结:")
print(f"1. GMM成功将鸢尾花数据集分为3个聚类,与真实类别数一致")
print(f"2. 调整兰德指数(ARI)为{ari:.4f},表明聚类结果与真实标签有较高一致性")
print(f"3. 轮廓系数为{silhouette:.4f},表明聚类内部紧凑且分离良好")
print(f"4. 平均聚类纯度为{np.mean(purity_scores):.4f},说明大多数样本被正确分组")
print(f"5. 最佳协方差类型为'{results_df.loc[results_df['ARI'].idxmax(), '协方差类型']}'")
print(f"6. 信息准则(AIC/BIC)确认3个聚类是最合适的")
四、GMM的关键特点总结
-
概率基础:不是简单的几何划分,而是基于概率模型的统计推断
-
软分配:允许数据点以不同概率属于多个聚类
-
形状灵活:可以识别各种形状和方向的聚类
-
不确定性量化:可以提供聚类分配的置信度
-
生成能力:不仅聚类,还能生成新的类似数据
-
统计严谨:有严格的理论基础和模型选择标准
-
自然解释:聚类结果可以解释为数据生成机制
GMM的核心魅力在于它将聚类从简单的"分组"提升到了"理解数据生成过程"的层面,为我们提供了一种更深刻、更灵活、更符合现实世界模糊性的数据分析工具。




















 701
701

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








