文章较长,示例代码在第三个部分,如需要数据及源码,关注微信公众号【爱敲代码的破晓】,关注微信公众号,后台私信【20251230】
一、DBSCAN聚类原理
1. 核心思想
-
基于密度:DBSCAN通过寻找数据空间中高密度区域来发现簇,不同于基于距离划分的方法(如K-means)
-
噪声容忍:能够识别并处理数据中的噪声点和异常值
-
形状无关:可以发现任意形状的簇,不限于球形或凸形
2. 核心概念
-
ε-邻域:以数据点为中心、ε为半径的圆形区域
-
核心点:ε-邻域内包含至少MinPts个点的数据点
-
边界点:ε-邻域内点数少于MinPts,但位于核心点邻域内的点
-
噪声点/离群点:既不是核心点也不是边界点的点
3. 聚类过程
-
参数设定:设定邻域半径ε和最小点数MinPts
-
核心点识别:遍历所有点,找出所有核心点
-
密度可达性扩展:
-
从任一未访问的核心点出发
-
递归寻找所有密度可达的点(通过一系列核心点相连)
-
将所有密度可达的点归为同一簇
-
-
重复扩展:重复步骤3,直到所有核心点都被访问
-
噪声处理:剩余未归类的点标记为噪声
4. 关键特性
-
无需预设簇数:自动发现数据中的自然聚类
-
密度驱动:基于局部密度而非全局距离
-
连通性传播:通过密度可达性传播簇的成员关系
-
异常值检测:天然具备异常检测能力
5. 算法特点
-
确定性:给定参数,结果是确定的(除了边界点归属可能有歧义)
-
效率:时间复杂度通常为O(n log n),适合中等规模数据集
-
稳定性:对输入顺序相对不敏感
二、与其他聚类算法的对比优势
相对于K-means的优势
1. 无需指定簇数量
-
K-means:必须预先指定K值,选择不当会导致结果失真
-
DBSCAN:自动确定簇的数量,更符合数据自然结构
2. 处理任意形状的簇
-
K-means:假设簇是球形或凸形,对复杂形状效果差
-
DBSCAN:可以发现任意形状的簇,包括非凸形、线形、环形等
3. 噪声和异常值处理
-
K-means:强制将所有点分配到簇,异常值会扭曲质心位置
-
DBSCAN:明确识别噪声点,提高主簇的纯净度
4. 对初始值不敏感
-
K-means:结果受初始质心选择影响大,可能收敛到局部最优
-
DBSCAN:结果基本由数据密度决定,重复性更好
5. 无需距离度量假设
-
K-means:通常使用欧氏距离,对尺度敏感
-
DBSCAN:可以使用各种距离度量,更灵活
相对于层次聚类的优势
1. 计算效率
-
层次聚类:时间复杂度O(n³)或O(n² log n),不适合大数据集
-
DBSCAN:时间复杂度O(n log n),效率更高
2. 无需存储距离矩阵
-
层次聚类:需要存储和维护距离矩阵,内存消耗大
-
DBSCAN:基于邻域查询,内存效率更高
3. 清晰的聚类边界
-
层次聚类:需要人工选择切割层次,边界模糊
-
DBSCAN:基于密度阈值,边界更明确
4. 噪声处理能力
-
层次聚类:通常将所有点纳入聚类树
-
DBSCAN:明确分离噪声,结果更干净
相对于高斯混合模型(GMM)的优势
1. 无分布假设
-
GMM:假设数据来自高斯分布的混合
-
DBSCAN:无分布假设,适用范围更广
2. 簇形状更灵活
-
GMM:只能发现椭球形簇
-
DBSCAN:可以发现任意形状的簇
3. 参数解释性
-
GMM:参数(均值、协方差)复杂,解释困难
-
DBSCAN:参数(ε, MinPts)直观,易于理解和调整
4. 异常检测
-
GMM:异常检测需要额外处理
-
DBSCAN:异常检测是算法的自然组成部分
相对于谱聚类的优势
1. 参数更少
-
谱聚类:需要构建相似矩阵、选择特征向量数量等
-
DBSCAN:主要参数只有ε和MinPts
2. 计算复杂度低
-
谱聚类:涉及特征值分解,计算成本高
-
DBSCAN:基于邻域查询,计算更高效
3. 无需降维假设
-
谱聚类:依赖数据在特征空间的低维嵌入
-
DBSCAN:直接在原始空间操作
三、代码示例
1. 导入第三方库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import (
adjusted_rand_score,
normalized_mutual_info_score,
silhouette_score,
calinski_harabasz_score,
davies_bouldin_score,
confusion_matrix,
classification_report
)
from scipy.optimize import linear_sum_assignment # 替代sklearn.utils.linear_assignment_
import os
import warnings
warnings.filterwarnings('ignore')
2.绘图设置
# 创建输出目录
output_dir = "dbscan_iris_results"
os.makedirs(output_dir, exist_ok=True)
# 设置中文字体(如果系统支持)
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
3.加载数据
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("=" * 60)
print("鸢尾花数据集信息")
print("=" * 60)
print(f"数据集形状: {X.shape}")
print(f"特征名称: {feature_names}")
print(f"目标类别: {target_names}")
print(f"样本分布: {np.bincount(y)}")
4.数据标准化
# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
5.构造DBSCAN参数
# DBSCAN参数调优 - 尝试不同的eps和min_samples组合
param_grid = {
'eps': [0.3, 0.5, 0.7, 1.0, 1.2, 1.5],
'min_samples': [3, 4, 5, 7, 10]
}
best_score = -1
best_params = {}
print("\n" + "=" * 60)
print("DBSCAN参数调优过程")
print("=" * 60)
# 保存参数调优结果
param_results = []
6.训练并确定最佳模型
for eps in param_grid['eps']:
for min_samples in param_grid['min_samples']:
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
# 计算轮廓系数(排除噪声点)
if len(set(labels)) > 1 and -1 in labels:
# 如果有噪声点,只计算非噪声点的轮廓系数
if sum(mask) > 1: # 至少需要两个非噪声点
score = silhouette_score(X_scaled[mask], labels[mask])
else:
score = -1
elif len(set(labels)) > 1:
# 没有噪声点,使用所有点
score = silhouette_score(X_scaled, labels)
else:
score = -1
# 打印当前参数的结果
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)
param_results.append({
'eps': eps,
'min_samples': min_samples,
'n_clusters': n_clusters,
'n_noise': n_noise,
'score': score
})
if score > best_score:
best_score = score
best_params = {'eps': eps, 'min_samples': min_samples}
best_labels = labels.copy()
print(f"eps={eps:.1f}, min_samples={min_samples:2d} => "
f"聚类数={n_clusters}, 噪声点={n_noise}, 轮廓系数={score:.4f}")
print("\n" + "=" * 60)
print(f"最佳参数: eps={best_params['eps']}, min_samples={best_params['min_samples']}")
print(f"最佳轮廓系数: {best_score:.4f}")
# 使用最佳参数训练DBSCAN模型
best_dbscan = DBSCAN(eps=best_params['eps'], min_samples=best_params['min_samples'])
dbscan_labels = best_dbscan.fit_predict(X_scaled)
7.打印分类结果
#析聚类结果
n_clusters = len(set(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)
n_noise = list(dbscan_labels).count(-1)
print("\n" + "=" * 60)
print("DBSCAN聚类结果分析")
print("=" * 60)
print(f"聚类数量: {n_clusters}")
print(f"噪声点数量: {n_noise}")
print(f"噪声点比例: {n_noise/len(dbscan_labels)*100:.2f}%")
print(f"各簇样本数: {np.bincount(dbscan_labels[dbscan_labels >= 0])}")
8.打印分类结果
# 评估指标计算
print("\n" + "=" * 60)
print("聚类效果评估")
print("=" * 60)
# 1. 外部指标(与真实标签对比)
if n_clusters > 0:
# 调整兰德指数(ARI)
print(f"调整兰德指数(ARI): {ari:.4f}")
# 归一化互信息(NMI)
nmi = normalized_mutual_info_score(y, dbscan_labels)
print(f"归一化互信息(NMI): {nmi:.4f}")
# 2. 内部指标
if n_clusters > 1:
# 轮廓系数
if -1 in dbscan_labels:
silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])
else:
silhouette = silhouette_score(X_scaled, dbscan_labels)
print(f"轮廓系数(Silhouette): {silhouette:.4f}")
# Calinski-Harabasz指数
if -1 in dbscan_labels:
ch_score = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])
else:
ch_score = calinski_harabasz_score(X_scaled, dbscan_labels)
print(f"Calinski-Harabasz指数: {ch_score:.4f}")
# Davies-Bouldin指数
if -1 in dbscan_labels:
db_score = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])
else:
db_score = davies_bouldin_score(X_scaled, dbscan_labels)
print(f"Davies-Bouldin指数: {db_score:.4f}")
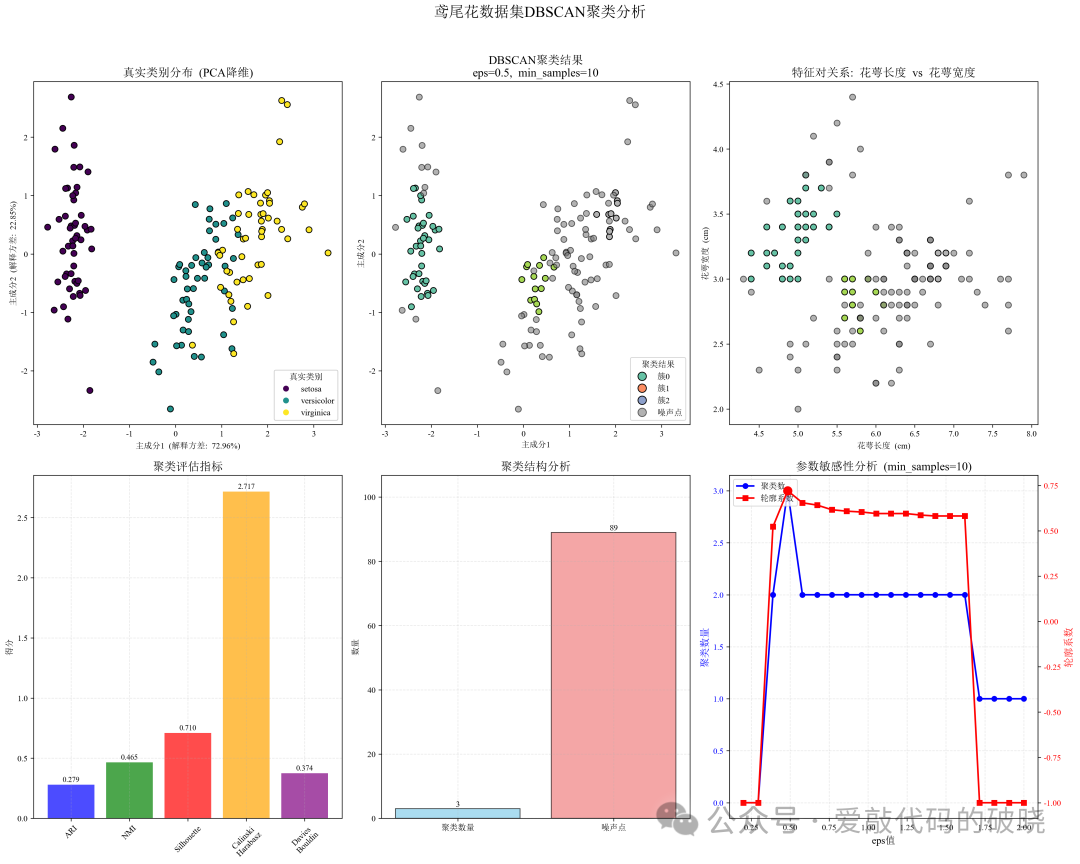
9.数据可视化
# 可视化部分
fig = plt.figure(figsize=(18, 14))
# 使用PCA降维到2D以便可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# 1. 真实类别可视化
ax1 = plt.subplot(2, 3, 1)
scatter1 = ax1.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
ax1.set_title('真实类别分布 (PCA降维)', fontsize=14, fontweight='bold')
ax1.set_xlabel('主成分1 (解释方差: {:.2f}%)'.format(pca.explained_variance_ratio_[0]*100))
ax1.set_ylabel('主成分2 (解释方差: {:.2f}%)'.format(pca.explained_variance_ratio_[1]*100))
legend1 = ax1.legend(handles=scatter1.legend_elements()[0], labels=list(target_names), title="真实类别")
ax1.add_artist(legend1)
# 2. DBSCAN聚类结果可视化
ax2 = plt.subplot(2, 3, 2)
# 为噪声点设置特殊颜色
if -1 in dbscan_labels:
# 噪声点用灰色表示
noise_mask = dbscan_labels == -1
# 先画簇点
scatter2a = ax2.scatter(X_pca[cluster_mask, 0], X_pca[cluster_mask, 1],
c=dbscan_labels[cluster_mask], cmap='Set2', edgecolor='k', s=50)
# 再画噪声点
scatter2b = ax2.scatter(X_pca[noise_mask, 0], X_pca[noise_mask, 1],
c='gray', edgecolor='k', s=50, alpha=0.6, label='噪声点')
# 创建图例
legend_elements = []
for i in range(n_clusters):
legend_elements.append(plt.Line2D([0], [0], marker='o', color='w',
markerfacecolor=colors[i], markeredgecolor='k',
markersize=10, label=f'簇{i}'))
legend_elements.append(plt.Line2D([0], [0], marker='o', color='w',
markerfacecolor='gray', markeredgecolor='k',
markersize=10, label='噪声点', alpha=0.6))
ax2.legend(handles=legend_elements, title="聚类结果")
else:
scatter2 = ax2.scatter(X_pca[:, 0], X_pca[:, 1], c=dbscan_labels, cmap='Set2', edgecolor='k', s=50)
ax2.legend(handles=scatter2.legend_elements()[0], labels=[f'簇{i}' for i in range(n_clusters)], title="聚类结果")
ax2.set_title(f'DBSCAN聚类结果\neps={best_params["eps"]}, min_samples={best_params["min_samples"]}',
fontsize=14, fontweight='bold')
ax2.set_xlabel('主成分1')
ax2.set_ylabel('主成分2')
# 3. 特征对关系图(前两个特征)
if -1 in dbscan_labels:
noise_mask = dbscan_labels == -1
scatter3a = ax3.scatter(X[cluster_mask, 0], X[cluster_mask, 1],
c=dbscan_labels[cluster_mask], cmap='Set2', edgecolor='k', s=50)
scatter3b = ax3.scatter(X[noise_mask, 0], X[noise_mask, 1],
c='gray', edgecolor='k', s=50, alpha=0.6)
else:
scatter3 = ax3.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='Set2', edgecolor='k', s=50)
ax3.set_title('特征对关系: 花萼长度 vs 花萼宽度', fontsize=14, fontweight='bold')
ax3.set_xlabel('花萼长度 (cm)')
ax3.set_ylabel('花萼宽度 (cm)')
# 4. 评估指标对比图
ax4 = plt.subplot(2, 3, 4)
metrics_names = ['ARI', 'NMI', 'Silhouette', 'Calinski\nHarabasz', 'Davies\nBouldin']
metrics_values = []
if n_clusters > 0:
metrics_values.append(ari)
metrics_values.append(nmi)
else:
metrics_values.extend([0, 0])
if n_clusters > 1:
metrics_values.append(silhouette)
metrics_values.append(ch_score / 100) # 缩小以便在图中显示
metrics_values.append(db_score)
else:
metrics_values.extend([0, 0, 0])
bars = ax4.bar(range(len(metrics_names)), metrics_values,
color=['blue', 'green', 'red', 'orange', 'purple'], alpha=0.7)
ax4.set_title('聚类评估指标', fontsize=14, fontweight='bold')
ax4.set_xticks(range(len(metrics_names)))
ax4.set_xticklabels(metrics_names, rotation=45, fontsize=10)
ax4.set_ylabel('得分')
ax4.grid(True, alpha=0.3, linestyle='--')
# 在柱状图上添加数值标签
for bar, val in zip(bars, metrics_values):
height = bar.get_height()
ax4.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{val:.3f}', ha='center', va='bottom', fontsize=9)
# 5. 聚类数量与噪声点分析
categories = ['聚类数量', '噪声点']
values = [n_clusters, n_noise]
colors_bar = ['skyblue', 'lightcoral']
bars2 = ax5.bar(categories, values, color=colors_bar, edgecolor='black', alpha=0.7)
ax5.set_title('聚类结构分析', fontsize=14, fontweight='bold')
ax5.set_ylabel('数量')
ax5.set_ylim(0, max(values) * 1.2)
ax5.grid(True, alpha=0.3, linestyle='--')
# 在柱状图上添加数值标签
for bar, val in zip(bars2, values):
height = bar.get_height()
ax5.text(bar.get_x() + bar.get_width()/2., height + 0.1,
str(val), ha='center', va='bottom', fontweight='bold')
# 6. 参数敏感性分析(固定min_samples,变化eps)
ax6 = plt.subplot(2, 3, 6)
eps_values = np.linspace(0.2, 2.0, 20)
n_clusters_list = []
silhouette_list = []
fixed_min_samples = best_params['min_samples']
for eps in eps_values:
dbscan_temp = DBSCAN(eps=eps, min_samples=fixed_min_samples)
labels_temp = dbscan_temp.fit_predict(X_scaled)
n_clusters_temp = len(set(labels_temp)) - (1 if -1 in labels_temp else 0)
n_clusters_list.append(n_clusters_temp)
# 计算轮廓系数
if n_clusters_temp > 1:
if -1 in labels_temp:
mask_temp = labels_temp != -1
if sum(mask_temp) > 1:
silhouette_temp = silhouette_score(X_scaled[mask_temp], labels_temp[mask_temp])
else:
silhouette_temp = -1
else:
silhouette_temp = silhouette_score(X_scaled, labels_temp)
else:
silhouette_temp = -1
silhouette_list.append(silhouette_temp)
line1 = ax6.plot(eps_values, n_clusters_list, 'b-', marker='o', label='聚类数', linewidth=2)
line2 = ax6_2.plot(eps_values, silhouette_list, 'r-', marker='s', label='轮廓系数', linewidth=2)
ax6.set_xlabel('eps值', fontsize=12)
ax6.set_ylabel('聚类数量', color='b', fontsize=12)
ax6_2.set_ylabel('轮廓系数', color='r', fontsize=12)
ax6.set_title(f'参数敏感性分析 (min_samples={fixed_min_samples})', fontsize=14, fontweight='bold')
ax6.tick_params(axis='y', labelcolor='b')
ax6_2.tick_params(axis='y', labelcolor='r')
ax6.grid(True, alpha=0.3, linestyle='--')
# 标记最佳参数点
best_eps_idx = np.argmin(np.abs(eps_values - best_params['eps']))
ax6.plot(eps_values[best_eps_idx], n_clusters_list[best_eps_idx], 'bo', markersize=10, label='最佳参数')
ax6_2.plot(eps_values[best_eps_idx], silhouette_list[best_eps_idx], 'ro', markersize=10)
# 合并图例
labels = [l.get_label() for l in lines]
ax6.legend(lines, labels, loc='upper left')
# 添加总标题
plt.suptitle('鸢尾花数据集DBSCAN聚类分析', fontsize=18, fontweight='bold', y=1.02)
plt.tight_layout()
# 保存图形
plt.savefig(os.path.join(output_dir, 'dbscan_iris_clustering_analysis.png'),
dpi=300, bbox_inches='tight', facecolor='white')
plt.savefig(os.path.join(output_dir, 'dbscan_iris_clustering_analysis.pdf'),
bbox_inches='tight', facecolor='white')
print(f"\n主分析图已保存至: {output_dir}/dbscan_iris_clustering_analysis.png 和 .pdf")
plt.show()
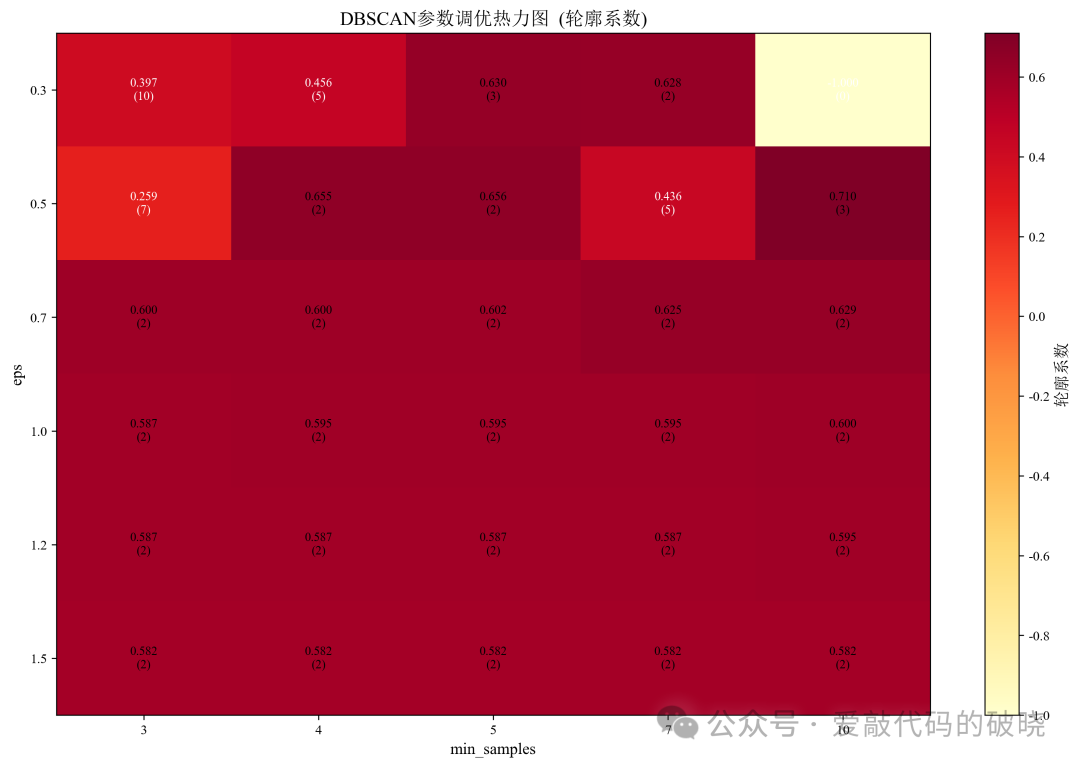
# 参数调优结果可视化
fig2, ax = plt.subplots(figsize=(12, 8))
param_df = pd.DataFrame(param_results)
# 创建热力图数据
heatmap_data = pd.pivot_table(param_df, values='score',
index='eps', columns='min_samples')
clusters_data = pd.pivot_table(param_df, values='n_clusters',
index='eps', columns='min_samples')
# 绘制热力图
im = ax.imshow(heatmap_data.values, cmap='YlOrRd', aspect='auto')
ax.set_xticks(range(len(param_grid['min_samples'])))
ax.set_yticks(range(len(param_grid['eps'])))
ax.set_xticklabels(param_grid['min_samples'])
ax.set_yticklabels(param_grid['eps'])
ax.set_xlabel('min_samples', fontsize=12)
ax.set_ylabel('eps', fontsize=12)
ax.set_title('DBSCAN参数调优热力图 (轮廓系数)', fontsize=14, fontweight='bold')
# 添加颜色条
cbar = plt.colorbar(im, ax=ax)
cbar.set_label('轮廓系数', fontsize=12)
# 在每个单元格中添加数值
for i in range(len(param_grid['eps'])):
for j in range(len(param_grid['min_samples'])):
score = heatmap_data.values[i, j]
n_clusters = clusters_data.values[i, j]
ax.text(j, i, f'{score:.3f}\n({n_clusters})',
ha='center', va='center',
color='black' if score > 0.5 else 'white', fontsize=9)
plt.tight_layout()
plt.savefig(os.path.join(output_dir, 'dbscan_parameter_heatmap.png'),
dpi=300, bbox_inches='tight', facecolor='white')
print(f"参数调优热力图已保存至: {output_dir}/dbscan_parameter_heatmap.png")
plt.show()
10.综合评估与结果保存
# 聚类结果详细对比分析
print("\n" + "=" * 60)
print("聚类结果与真实标签的详细对比")
print("=" * 60)
# 创建结果DataFrame
results_df = pd.DataFrame({
'花萼长度': X[:, 0],
'花萼宽度': X[:, 1],
'花瓣长度': X[:, 2],
'花瓣宽度': X[:, 3],
'真实类别': y,
'真实类别名称': [target_names[label] for label in y],
'聚类标签': dbscan_labels,
'聚类类别': ['噪声' if label == -1 else f'簇{label}' for label in dbscan_labels]
})
# 保存结果到CSV
results_df.to_csv(os.path.join(output_dir, 'dbscan_clustering_results.csv'), index=False, encoding='utf-8-sig')
print(f"聚类结果详情已保存至: {output_dir}/dbscan_clustering_results.csv")
# 统计每个真实类别中聚类标签的分布
print("\n真实类别 vs 聚类标签分布:")
print(cluster_distribution)
# 计算聚类准确率(将每个聚类映射到最常见的真实类别)
if n_clusters > 0:
# 创建一个映射函数
from scipy.stats import mode
# 为每个聚类找到最常见的真实类别(排除噪声点)
cluster_to_true_mapping = {}
for cluster_id in range(n_clusters):
mask = (dbscan_labels == cluster_id)
if sum(mask) > 0:
true_labels_in_cluster = y[mask]
# 使用兼容不同scipy版本的mode函数调用
try:
# 尝试新版本的调用方式
mode_result = mode(true_labels_in_cluster, keepdims=False)
most_common_label = mode_result.mode
except TypeError:
# 如果失败,使用旧版本的调用方式
most_common_label = mode_result.mode[0] if hasattr(mode_result.mode, '__len__') else mode_result.mode
cluster_to_true_mapping[cluster_id] = most_common_label
# 计算准确率(排除噪声点)
correct_predictions = 0
total_non_noise = 0
for i in range(len(dbscan_labels)):
cluster_id = dbscan_labels[i]
if cluster_id != -1: # 排除噪声点
if cluster_id in cluster_to_true_mapping:
if y[i] == cluster_to_true_mapping[cluster_id]:
correct_predictions += 1
if total_non_noise > 0:
accuracy = correct_predictions / total_non_noise
print(f"\n聚类准确率(排除噪声点): {accuracy:.4f} ({correct_predictions}/{total_non_noise})")
# 分析DBSCAN的优缺点
print("\n" + "=" * 60)
print("DBSCAN在鸢尾花数据集上的表现分析")
print("=" * 60)
print("优点:")
print("1. 不需要预先指定聚类数量")
print("2. 能够识别噪声点和异常值")
print("3. 可以发现任意形状的簇")
print("\n缺点:")
print("1. 对参数eps和min_samples敏感")
print("2. 在高维数据上可能表现不佳(维度灾难)")
print("3. 当簇的密度差异较大时,难以选择合适参数")
print("\n建议:")
print("1. 对数据进行标准化处理")
print("2. 使用网格搜索或参数敏感性分析选择合适参数")
print("3. 考虑使用降维技术处理高维数据")
print("4. 结合领域知识调整参数")
# 保存评估指标
with open(os.path.join(output_dir, 'evaluation_results.txt'), 'w', encoding='utf-8') as f:
f.write("=" * 60 + "\n")
f.write("鸢尾花数据集DBSCAN聚类分析结果\n")
f.write("=" * 60 + "\n\n")
f.write(f"最佳参数: eps={best_params['eps']}, min_samples={best_params['min_samples']}\n")
f.write(f"聚类数量: {n_clusters}\n")
f.write(f"噪声点数量: {n_noise} ({n_noise/len(dbscan_labels)*100:.2f}%)\n\n")
if n_clusters > 0:
f.write(f"调整兰德指数(ARI): {ari:.4f}\n")
f.write(f"归一化互信息(NMI): {nmi:.4f}\n")
if n_clusters > 1:
f.write(f"轮廓系数(Silhouette): {silhouette:.4f}\n")
f.write(f"Calinski-Harabasz指数: {ch_score:.4f}\n")
f.write(f"Davies-Bouldin指数: {db_score:.4f}\n")
print(f"\n所有结果已保存至目录: {output_dir}/")
print("包括:")
print("1. 主分析图 (dbscan_iris_clustering_analysis.png/pdf)")
print("2. 参数调优热力图 (dbscan_parameter_heatmap.png)")
print("3. 聚类结果详情 (dbscan_clustering_results.csv)")
print("4. 评估指标 (evaluation_results.txt)")
四、总结
1.DBSCAN特点
-
适应性:适用于各种形状和大小的簇
-
鲁棒性:对噪声和异常值具有天然抵抗力
-
自动化:无需预先指定聚类数量
-
直观性:参数物理意义明确,易于解释
-
实用性:在真实世界数据中表现良好,尤其是当数据包含噪声和非球形簇时
-
可扩展性:有高效的实现版本,适合处理中等规模数据集
-
多功能性:同时完成聚类和异常检测两项任务
2.DBSCAN适用场景
-
数据包含噪声和异常值
-
簇的形状不规则或密度不均
-
不确定簇的数量
-
需要发现数据中的自然分组
-
同时需要聚类和异常检测
3.DBSCAN局限性
-
对参数ε和MinPts敏感
-
在高维数据上效果可能下降(维度灾难)
-
当簇的密度差异很大时,难以找到合适的全局参数
-
边界点的归属可能不明确
DBSCAN的核心理念"基于密度连接"使其成为处理复杂、含噪声数据集的强大工具,特别适用于那些传统基于距离或质心的算法难以处理的情况。




















 662
662

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








