Attention的矩阵表示及理解

最新推荐文章于 2025-01-15 22:59:36 发布

原创

最新推荐文章于 2025-01-15 22:59:36 发布 · 4.7k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#pytorch #机器学习 #深度学习 #神经网络 #自然语言处理

本文详细介绍了注意力机制在深度学习，特别是Seq2Seq模型中的应用。通过对比Luong和Vaswani的注意力机制，重点解释了Scaled Dot-Product Attention的工作原理，包括Attention Score的计算、Attention Distribution的softmax转换以及Attention Output的生成过程。文中还提供了矩阵运算的表示，帮助读者理解各个步骤，并给出了PyTorch实现的关键代码片段。

Attention两篇文章链接：其中一个是Luong,提的dot product attention，另一个是Vaswali的scaled dot product attention ，也就是大名鼎鼎的attention is all you need。

说到attention不再过多赘述，论文中的公式推导感觉比较简单，结合自己的理解写一下矩阵层面的表示。数学好的可以跳过。

在attention is all you need这篇文章中，他是这么写的：
$softmax(\frac{QK^T}{\sqrt{d_k}})V$ ，而Luong那篇文章中，公式比较多且分散。
但无论如何，大致总结是（看下图），先算attention score（Q，K相乘），再用softmax算distribution，再把distribution和hidden state相乘获得attention output（最上面那个MatMul），再把output和另一个hidden相加（concat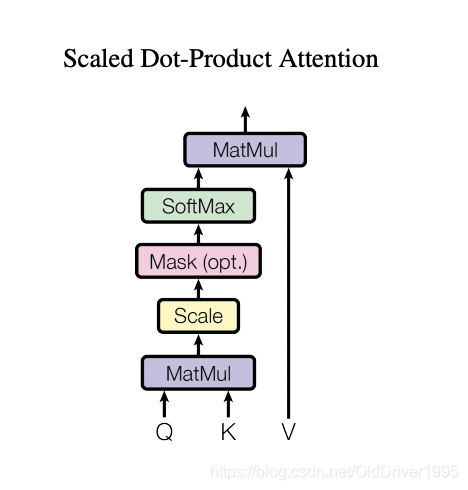）。在这里插入图片描述

这里以seq2seq模型中的attention为例。

首先我们有encoder hidden state的一个序列: $H =[h_1, h_2, ...h_N]$
然后有 $t$ 时刻的decoder state $s^t$ , 所有时刻的decoder state就是 $S=[s^1, s^2, ..., s^t]$ 。
每次用所有的encoder hidden state去和当前时刻的decoder state相乘（dot product）

对于 $t$ 时刻而言的attention score就是用 $e^t = [h_1^Ts^t, h_2^Ts^t, ..., h_N^Ts^t]$ ，
但实际在计算中，我们是把整个decoder hidden state和encoder hidden state乘起来，而不是像循环一样对每个时刻都依次计算
$\left[ \begin{matrix} h_1^Ts^1 & h_2^Ts^1, &..., &h_N^Ts^1 \\ \vdots & \vdots &\ddots &\vdots\\ h_1^Ts^{t-1} & h_2^Ts^{t-1}, &..., &h_N^Ts^{t-1}\\ h_1^Ts^t & h_2^Ts^t, &..., &h_N^Ts^t \end{matrix} \right] = \left[ \begin{matrix}s^1\\ s^2\\ \vdots\\ s^t \end{matrix} \right] \cdot \left[ \begin{matrix} h_1^T & h_2^T & \cdots & & h_N^T \end{matrix} \right] \ (1)$