2021李宏毅机器学习之Self-attention（矩阵角度）

从矩阵的角度讲解Self-Attention的过程

下来我们从矩阵乘法的角度,再重新讲一次我们刚才讲的,Self-attention 是怎麼运作的。我们现在已经知道每一个 a 都产生 q k v。如果要用矩阵运算表示这个操作的话,是什么样子呢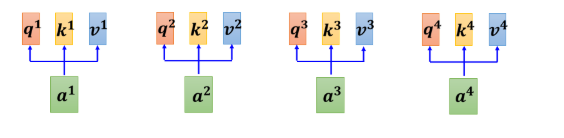
我们每一个 a,都乘上一个矩阵,我们这边用 W^q 来表示它,得到 qⁱ,每一个 a 都要乘上 W^q,得到qⁱ,这些不同的 a 你可以把它合起来,当作一个矩阵来看待

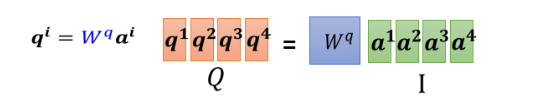
 一样a²a³a⁴也都乘上W^q得到q²q³跟q⁴ ,那你可以把 a¹ 到 a⁴ 拼起来,看作是一个矩阵,这个矩阵我们用 I 来表示，这个矩阵的四个 column 就是a¹到a⁴,I乘上W^q 就得到另外一个矩阵,我们用 Q来表示它,这个Q 就是把q¹到q⁴这四个 vector 拼起来,就是Q的四个 column.
 所以我们从 $a^1$ 到 $a^4$,得到 $q^1$ 到 $q^4$这个操作,其实就是把 I 这个矩阵,乘上另外一个矩阵 $W^q$，得到矩阵$Q$。$I$ 这个矩阵它裡面的 column就是我们 Self-attention 的 input是 $a^1$ 到 $a^4$；$W^q$其实是 network 的参数,它是等一下会被learn出来的 ；$Q$ 的四个 column,就是 $q^1$ 到 $q^4$
 接下来產生 k 跟 v 的操作跟 q 是一模一样的

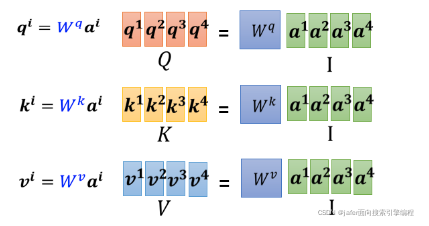
 所以每一个 a 得到 q k v ,其实就是把输入的这个,vector sequence 乘上三个不同的矩阵,你就得到了 q,得到了 k,跟得到了 v
 下一步是,每一个 q 都会去跟每一个 k,去计算这个 inner product,去得到这个 attention 的分数,那得到 attention 分数这一件事情,如果从矩阵操作的角度来看,它在做什麼样的事情呢?

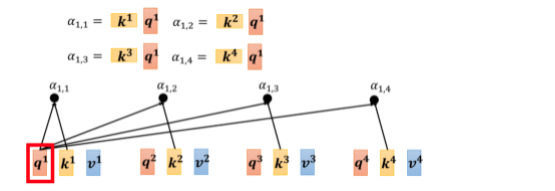
 你就是把 $q^1$ 跟 $k^1$ 做 inner product,得到 ${\alpha }_{1,1}$,所以 ${\alpha }_{1,1}$就是 $q^1$ 跟$k^1$ 的 inner product,那这边我就把这个,$k^1$它背后的这个向量,把它画成比较宽一点代表说它是 transpose.
 同理 ${\alpha }_{1,2}$ 就是 $q^1$ 跟 $k^2$,做 inner product, ${\alpha }_{1,3}$ 就是 $q^1$ 跟 $k^3$ 做 inner product,这个 ${\alpha }_{1,4}$ 就是 $q^1$ 跟 $k^4$ 做 inner product,那这个四个步骤的操作,你其实可以把它拼起来,看作是矩阵跟向量相乘

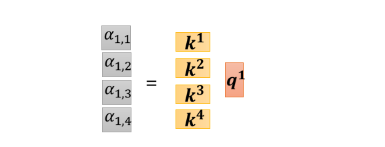
 这四个动作,你可以看作是我们把 $k^1$ 到 $k^4$ 拼起来,当作是一个矩阵的四个 row，那我们刚才讲过说,我们不只是 $q^1$,要对$k^1$ 到 $k^4$ 计算 attention,$q^2,q^3,q^4$也要对 $k^1$ 到 $k^4$ 计算 attention,操作其实都是一模一样的

 所以这些 attention 的分数可以看作是两个矩阵的相乘,一个矩阵它的 row,就是 $k^1$ 到 $k^4$,另外一个矩阵它的 column。我们会在 attention 的分数,做一下 normalization,比如说你会做 softmax,你会对这边的每一个 column,每一个 column 做 softmax,让每一个 column 裡面的值相加是 1。
 之前有讲过说 其实这边做 softmax不是唯一的选项,你完全可以选择其他的操作,比如说 ReLU 之类的,那其实得到的结果也不会比较差,通过了 softmax 以后,它得到的值有点不一样了,所以我们用 $A^{\prime }$,来表示通过 softmax 以后的结果
 我们已经计算出 $A^{\prime }$那我们把这个$v^1$ 到 $v^4$乘上这边的 α 以后,就可以得到 b

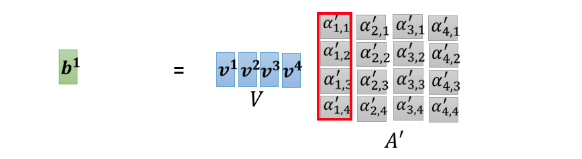
 你就把$v^1$ 到 $v^4$ 拼起来,你把 $v^1$ 到 $v^4$当成是V 这个矩阵的四个 column,把它拼起来,然后接下来你把 v 乘上,$A^{\prime }$ 的第一个 column 以后,你得到的结果就是 $b^1$。
 如果你熟悉线性代数的话,你知道说把这个 $A^{\prime }$ 乘上 V,就是把 $A^{\prime }$的第一个 column,乘上 V 这一个矩阵,你会得到你 output 矩阵的第一个 column。而把 A 的第一个 column乘上 V 这个矩阵做的事情,其实就是把 V 这个矩阵裡面的每一个 column,根据第 $A^{\prime }$ 这个矩阵裡面的每一个 column 裡面每一个 element,做 weighted sum,那就得到 $b^1$
 那就是这边的操作,把 $v^1$ 到 $v^4$ 乘上 weight,全部加起来得到 $b^1$,
 如果你是用矩阵操作的角度来看它,就是把$ A’$ 的第一个 column 乘上 V,就得到 $b^1$,然后接下来就是以此类推

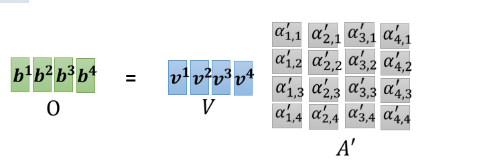
 就是以此类推,把 $A^{\prime }$ 的第二个 column 乘上 V,就得到 $b^2$,$A^{\prime }$ 的第三个 column 乘上 V 就得到 $b^3$,$A^{\prime }$ 的最后一个 column 乘上 V,就得到 $b^4$。所以我们等於就是把 $A^{\prime }$ 这个矩阵,乘上 V 这个矩阵,得到 O 这个矩阵,O 这个矩阵裡面的每一个 column,就是 Self-attention 的输出,也就是 $b^1$ 到 $b^4$。

矩阵角度小结

 所以其实整个 Self-attention,我们在讲操作的时候,我们在最开始的时候 跟你讲的时候我们讲说,我们先產生了 q k v,然后再根据这个 q 去找出相关的位置,然后再对 v 做 weighted sum,其实这一串操作,就是一连串矩阵的乘法而已。
 我们再复习一下我们刚才看到的矩阵乘法

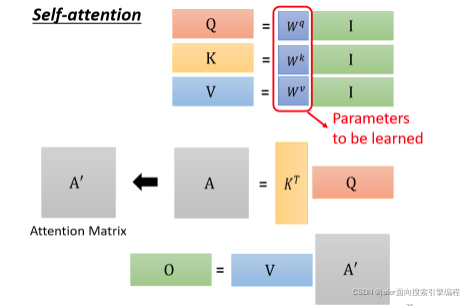
• I 是 Self-attention 的 input,Self-attention 的 input 是一排的vector,这排 vector 拼起来当作矩阵的 column,就是 I

• 这个 input 分别乘上三个矩阵,$W^q$ $W^k$ 跟$ W^v$,得到 Q K V

• 这三个矩阵,接下来 Q 乘上 K 的 transpose,得到 A 这个矩阵,A 的矩阵你可能会做一些处理,得到 $A^{\prime }$,那有时候我们会把这个 $A^{\prime }$,叫做 Attention Matrix，生成Q矩阵就是为了得到Attention的score

• 然后接下来你把 $A^{\prime }$ 再乘上 V,就得到 O,O 就是 Self-attention 这个 layer 的输出,生成V是为了计算最后的b，也就是矩阵O

 所以 Self-attention 输入是 I,输出是 O,那你会发现说虽然是叫 attention,但是其实 Self-attention layer 裡面,唯一需要学的参数,就只有 $W^q$ $W^k$ 跟$ W^v$ 而已,只有$W^q$ $W^k$ 跟$ W^v$是未知的,是需要透过我们的训练资料把它找出来的。
 但是其他的操作都没有未知的参数,都是我们人為设定好的,都不需要透过 training data 找出来,那这整个就是 Self-attention 的操作,从 I 到 O 就是做了 Self-attention

以上内容都是参考自：https://github.com/unclestrong/DeepLearning_LHY21_Notes