线性代数：矩阵的 秩和逆

正文

1、矩阵的行最简形式的一般形式

上一章节引入了矩阵的 $行空间$ 和 $列空间$，其中矩阵的行空间的维度就是行秩，矩阵的列空间的维度就是列秩。
其实，对于一个任意形状的矩阵，都有矩阵行秩 = 矩阵的列秩
证明如下:
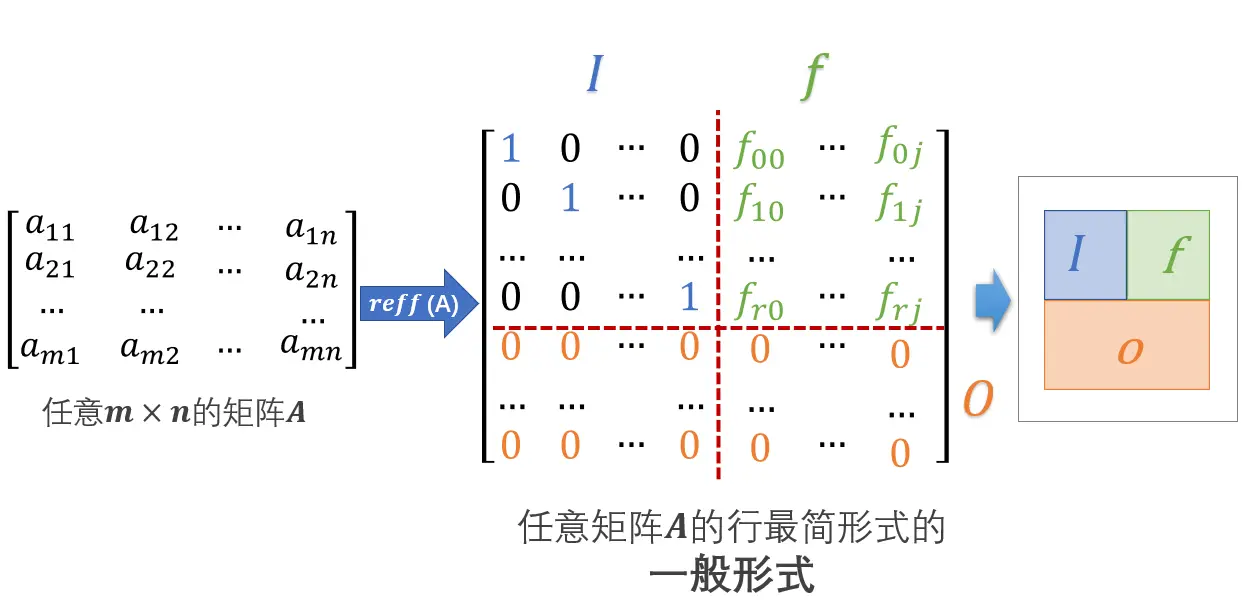
首先，对于任意一个$m$行$n$列的矩阵$A$，通过高斯消元和列交换后可以化成如下一般形式的行最简形式:

将一个矩阵化为行最简形式后，如果矩阵的行最简形式有全零行，这些零行一定都放在行最简形式的下面，对应上面图示$reff(A)$矩阵中的$O$部分；全零行上面的部分都是非零行，非零行也可以分成两部分$I$矩阵和$f$矩阵,其中左侧的$I$矩阵是单位矩阵，右侧的$f$矩阵的是一个没有规律的任意矩阵。其实这个一般形式的$reff(A)$矩阵上面的$I$和$f$两部分分别对应矩阵行最简形式的 主元列(pivot) 和 自由列(free column)。

从矩阵的行最简形式的一般形式可以看出，对于任意一个矩阵，先通过高斯消元后，再经过一定的列变换把主元列往左侧靠,最终这个矩阵的行最简形式的左上部分一定会形成一个单位矩阵$I$的形状。

既然一个矩阵的行最简形式中所有的主元列紧密排列在一起后会形成一个单位矩阵$I$,又因为单位矩阵一定是一个方阵，所以如果一个矩阵的行最简形式中非零行有$r$行的的话，那么这个矩阵的主元列也就一定有$r$列。
这样一来通过这个左上角的单位矩阵$I$，就可以看出矩阵化为行最简形式后，它的非零行数一定等于主元列数。因此对于一个任意形状的矩阵，都有矩阵行秩 = 矩阵的列秩这样的性质。

广义来说矩阵的行最简形式的一般形式通常写成：$feff(A)=\left(\begin{array}{cc}I& f\\ O& O\end{array}\right)$

但是实际上，对于一个矩阵来说，

• 它的行最简形式可能没有非零行，所以它的行最简形式应该写成$feff(A)=\left(\begin{array}{cc}I& f\end{array}\right)$；
• 它的行最简形式也有可能没有自由列，那么它的行最简形式应该写成$feff(A)=\left(\begin{array}{c}I\\ O\end{array}\right)$；
• 它的行最简形式如果就是一个单位矩阵，它的行最简形式应该写成$feff(A)=\left(\begin{array}{c}I\end{array}\right)$。此时这个矩阵一定是一个可逆的矩阵，只有可逆的矩阵的行最简形式才是单位矩阵。

---

2、矩阵的秩

上面很好地说明了一个矩阵的行秩和列秩是相等的，所以它们可以统称为$矩阵的秩(Rank)$，一个矩阵的秩既是它的行秩也是列秩，因此可以说一个矩阵的行空间的和列空间的维度是相等的!

虽然根据矩阵的秩，可以推出一个矩阵的行空间的和列空间的维度是相等的，但是行空间的和列空间本身是不相等的。对于一个$m\times n$的矩阵来说，它的行空间是一个$n$维空间的子空间，而它的列空间是一个$m$维空间的子空间，因为行空间和列空间这两个空间所嵌套在的那个更大的空间都不一样，所以这两个空间也是不一样的。

对”矩阵的秩 =矩阵的行秩 = 矩阵的列秩“这条性质的一个具体应用示例: 快速判断一组向量生成的空间的维度

如计算向量$\vec{u}=(1,1,2),\vec{v}=(2,2,3),\vec{w}=(3,3,4)$的生成空间的维度的时候
将这些向量摞在一起形成矩阵来处理的时候，根据矩阵的秩的性质，其实可以不用考虑是按行方向进行排列还是列方向进行排列来形成矩阵，任意一种方法其实都可以。
假如按行方向排列这些向量可得$A=\left[\begin{array}{ccc}1& 1& 2\\ 2& 2& 3\\ 3& 3& 4\end{array}\right]$,那么向量生成的空间的维度就等价于矩阵$A$的行空间的维度，也就是行秩。
从行向量的的角度观察矩阵$A$，很难发现这个矩阵内向量相关性关系，但是从列的方向观察，可以很快就发现矩阵$A$的第1列和第2列的列向量是明显具有线性相关关系的，因此，这些向量生成的空间的维度一定不会大于2。

3、满秩

对于一个$n$阶方阵行空间是$n$维空间的子空间，列空间是$n$维空间的子空间。
当矩阵秩$r=n$的时候，
这个$n$ 阶方阵行空间和 列空间就都是 $n$ 维空间，
此时可以称这个$n$阶方阵为一个$满秩(FullRank)$ 的方阵，
这个矩阵有 $n$行$n$列，它的行最简形式的每一行都是非零行，每一列都是主元列，没有自由列，所以它的行最简形式为 $I$.