线性代数：矩阵的四子大子空间之 “零空间”

倪桦

已于 2024-11-23 15:24:46 修改

阅读量1.4k

点赞数 21

CC 4.0 BY-SA版权

分类专栏：线性代数文章标签：线性代数矩阵 python

于 2024-11-23 14:31:58 首次发布

本文链接：https://blog.youkuaiyun.com/Nh_code/article/details/143992010

线性代数专栏收录该内容

38 篇文章

订阅专栏

正文### 1、一个齐次线性方程组的所有解，形成一个向量空间

对于一个齐次线性方程组 $A x = O$ 来说，它的所有的解中每一解都是向量，那么把这些向量(齐次线性方程组的解)集合在一起形成一个空间，其实这个空间是一个向量空间。

这个结论可以证明如下：
对于一个齐次线性方程组 $A x = O$ ，它一定有解，因为至少会存在一个零解，所以它的所有解形成的空间不可能为空。

$\ 1$ 当这个齐次线性方程组只有唯一零解 的时候，意味着它的解形成的空间只有一个零向量，此时这个空间的维度为 $0$ ，空间内向量的加法和数量乘法满足封闭性，是一个向量空间，很容易得证。

$\ 2$ 当这个齐次线性方程组有无数解 的时候，求证它的解形成的空间是向量空间:
假设这个齐次线性系统的系数矩阵 $A$ 是一个 $m * n$ 的矩阵，那么它的每个解都是一个 $n$ 维向量(有序实数元组)。如果这些解形成的空间是向量空间，则一定是 $n$ 维空间( $Rn\color {darkred} {\small \textbf{ 欧几里得空间}} \ \ \ R^{n}$ 是向量空间)的子空间。

所以当证明齐次线性方程组的解形成的空间是 $n$ 维欧几里得空间的子空间，就说明它是一个向量空间。
$只需证明这个空间对向量加法和数量乘法封闭\color {darkred} {只需证明这个空间对向量加法和数量乘法封闭}$

（1）证明空间对向量加法封闭
假设向量 $u⃗\vec u$ 和 $v⃗\vec v$ 是齐次线性方程组 $A x = O$ 的两个解
就有 $\cdot \vec u = O, \ A \cdot \vec v = O \to A \cdot \vec u + A \cdot \vec v = O$ ；
进而可得 $\cdot (\vec u + \vec v) = O$ ；
上式子意味着两向量 $u⃗\vec u$ ， $v⃗\vec v$ 的和 $(u⃗+v⃗)(\vec u + \vec v)$ 也是这个齐次线性方程组的解;
因此对于齐次线性方程组的解形成的空间内任意取两个向量 $u⃗\vec u$ 和 $v⃗\vec v$ ， $u⃗+v⃗\vec u + \vec v$ 还是在这个空间内，所以该空间对向量加法封闭

（2）证明空间对向量的数量乘法封闭
假设向量 $u⃗\vec u$ 是齐次线性方程组 $A x = O$ 的一个解
就有 $\cdot \vec u = O$ , 这个等式两边同乘以一个实数 $k$ ，可得 $\cdot A \cdot (\vec u + \vec v) = k \cdot O = O$ ；
改写后可得 $\cdot (k \vec u) = O$ ；
上式子意味着向量 $ku⃗k\vec u$ 也是这个齐次线性方程组的解;
因此对于齐次线性方程组的解形成的空间内任意取一个向量 $u⃗\vec u$ ，那么这个 $u⃗\vec u$ 乘以任何一个实数 $k$ ，结果 $ku⃗k\vec u$ 还是在这个齐次线性方程组的解形成的空间内，所以该空间对数量乘法封闭。

>>综上，一个齐次线性方程组的所有解，形成一个向量空间得证

2、矩阵的零空间

$零空间\color{red} { 零空间}$ ：一个齐次线性方程组的所有解，形成一个向量空间，称这个空间为" $Space)\color{red} {\small 零空间 (Null \ Space)}$ "。

对于一个矩阵 $A$ 来说，它的零空间就是以 $A$ 为系数矩阵的齐次线性方程组 $A x = 0$ 中，这个线性系统所有的解 $x$ 组成的空间就是矩阵 $A$ 的零空间。

$零空间\color{red} { 零空间}$ 是矩阵的一个特殊的子空间,矩阵的零空间相比矩阵的行空间和列列空间要更加抽象，因为对于一个矩阵的行空间和列空间，我们可以直观的看到生成它们的就是这个矩阵的行向量和列向量，然后因为这些行向量和列向量可能线性相关，所以往往需要通过特殊的计算手段(对矩阵进行高斯消元求算矩阵的秩)来获得行空间和列空间的具体维度，进而能找到空间的一组基。相比之下，生成一个矩阵的零空间的向量，需要通过求解齐次线性方程组 $A x = 0$ 来获取。

对零空间的一些理解

对于线性系统 $A x = O$ ，所有的 $x$ 组成的空间是零空间。

如果把矩阵看成是向量的转换函数，那么对于等式 $A x = O$ ,其中系数矩阵A就可以看成是一个转换函数，零空间是一个集合，集合内的所有向量在A的变换下，都可以被映射到零点！
如果把矩阵看成是空间，那么就有零空间内任意向量和矩阵 $A$ 的行向量的点乘结果为0！
进一步推广，因为矩阵 $A$ 的行空间内的任意向量都由矩阵的行向量的线性组合所表示(如 $w⃗=k1u⃗+k2v⃗\vec w = k_1 \vec u + k_2 \vec v$ )，而零空间内任意向量和矩阵 $A$ 的行向量的点乘结果为 $0$ ，就有 $x⃗⋅w⃗=k1u⃗⋅x⃗+k2v⃗⋅x⃗=0\vec x \cdot \vec w = k_1 \vec u \cdot \vec x + k_2 \vec v \cdot \vec x = 0$ ，所以可以得出结论"对于零空间内的任意向量，和矩阵 $A$ 的行空间的任意向量的点乘结果为 $0$ " $这个结论其实表面，零空间内的所有向量，和矩阵A的行空间中的所有向量是垂直(正交)的。→\color {#0088b9} {\small {这个结论其实表面，零空间内的所有向量，和矩阵A的行空间中的所有向量是垂直(正交)的。}} \to$ 矩阵A的零空间与矩阵A的行空间正交。

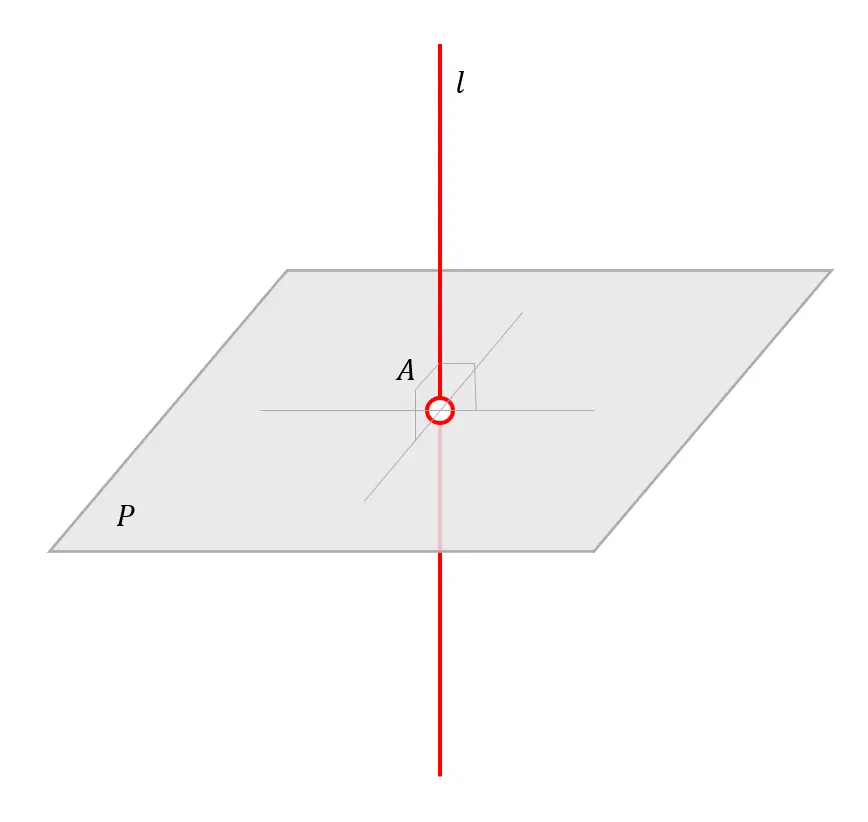
$三维空间中二维空间(平面)和一维空间(Line)的正交情况\large 三维空间中二维空间(平面)和一维空间(Line)的正交情况$

如果是对于两个平面(二维欧式空间)，它们在三维空间内是不可能正交的，它们只可能在四维空间中出现正交。

总结

矩阵 $A$ 的零空间
把 $A$ 看作是系统: $A$ 的零空间，就是 $A x = 0$ 中，所有x组成的空间。
把 $A$ 看作是函数(变换): $A$ 的零空间，所有被 $A$ 变化为 $0$ 点的所有向量组成的空间。
把 $A$ 看作是空间: $A$ 的零空间，是和 $A$ 的行空间正交的向量空间。