Games101-光线追踪（蒙特卡洛积分与路径追踪）

Reivew

渲染方程：看到的某点颜色等于自身发射的光，加上从四面八方反射的光

渲染里更多考虑连续性随机变量
随机变量x符合某一种概率密度分布f(x)
概率密度函数：非负，积分为1.
期望：值乘以概率密度加起来(或者积分)

Monte Carlo Integration/蒙特卡洛积分

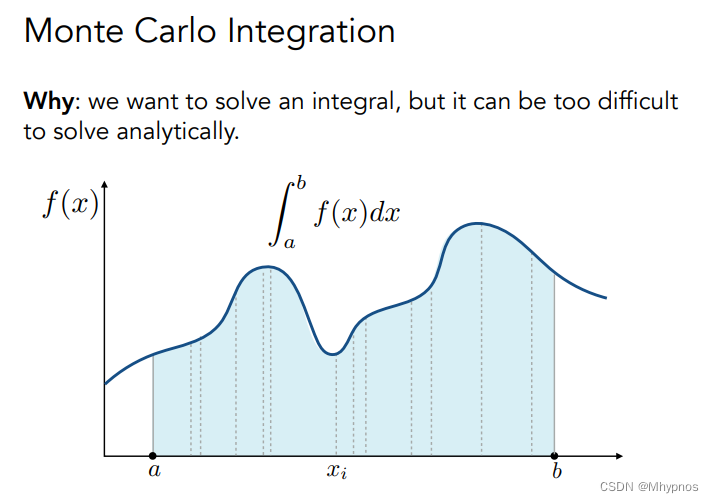
蒙特卡洛 是为了解定积分：从a~b函数下面围的面积

在ab之间随机取一个数$x_i$，得到对应的$f(x_i)$。假设整个曲线是要给长方形，长方形高为$f(x_i)$，宽度为$ab$，在ab间重复多次采样，将每次得到的长方形平均即为结果

在积分域$ab$间随机采样一个位置，可以定义任何一个概率密度来采样，采样出位置$x_i$，蒙特卡洛表示积分可以近似成$\frac{f(x)}{p(x)}$的求和平均

例子：假设在ab间均匀采样，则采样用的PDF各处相同，是个常数C

根据蒙特卡洛积分随机采样，采样得到$x_i$，对应的$p(x)$为$\frac{1}{b-a}$
得到的结果就是之前的定义：随便取一个x，找到高度，乘以b-a，得到一个矩形，再把所有采样的矩形求平均

不管如何采样，只要有一个满足的PDF，求可以求到定积分的近似

只需要能够在ab间以一种方式进行采样，只要知道采样对应的PDF就可求积分。不用关心积分域是多少，因为积分域已经在PDF里体现出来了

性质：

1. 采样数越多，方差越小，得到的结果越准
2. 对x采样，对x积分

Path Tr