一文看懂逻辑回归

看了一些介绍逻辑回归的文章，这里通过一个例子的贯穿做一下知识点的整合巩固，如有遗漏或不合理的地方欢迎讨论交流。

问题引入与模型建构

现有20个学生投入0-6个小时学习课程的记录，分析投入时间和是否通过考试的概率的关系。在这个问题中是否通过考试只有两种结果：通过和不通过。可以用虚拟变量1和0分别表示。我们用y代表已知的考试结果，x为已知的投入时间，发现其中还有一个隐藏变量：知识掌握程度，可以先设为z，假设z(x)线性变化，当然z(x)的具体表达式暂时未知，需要通过学习来获得。而对分类问题的预测其本质是建立在z(x)的基础上的。这一点很多文章并没有讲清楚，但对于算法的理解至关重要。
他们之间的关系是z(x)，y(z)。同时选用sigmoid 函数作为合理的y(z)的关系。

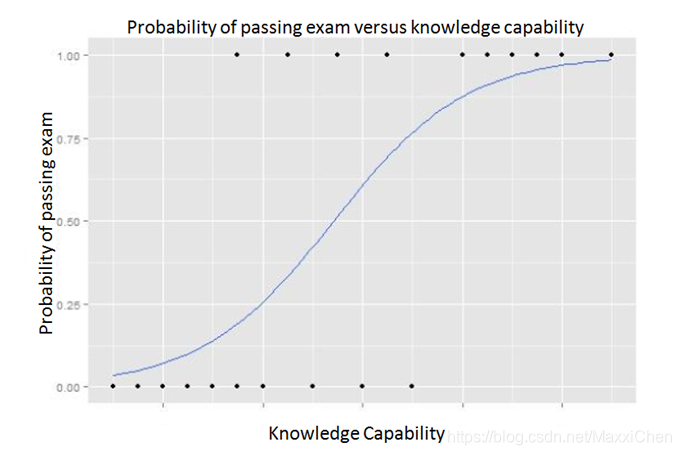
模型构建

在介绍Logistic Regression之前我们先简单说一下线性回归，线性回归的主要思想就是通过历史数据拟合出一条直线，用这条直线对新的数据进行预测，线性回归可以参考我之前的一篇文章。
这里直接给出公式(这里简短插一句，我觉得应该写成X^T*Theta的形式，因为Theta才是主变量):
$$\begin{gathered} z(x)=b+wx=\left(\begin{array}{cc}b& w\end{array}\right)\left(\begin{array}{c}1\\ x\end{array}\right)={\Theta }^{T}X \\ Pr(y=1|X;\Theta )=y(z)=h_{\Theta }(z)=\frac{1}{1+e^{-z}} \\ Pr(y=0|X;\Theta )=1-h_{\Theta }(z) \end{gathered}$$
直观描述为：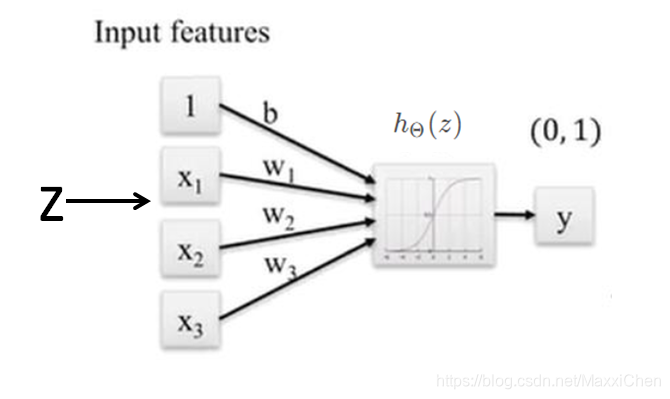
Sigmod函数的作用是将线性函数的结果映射到了[0,1]的范围中，即可以用来表达分类的概率0-100%

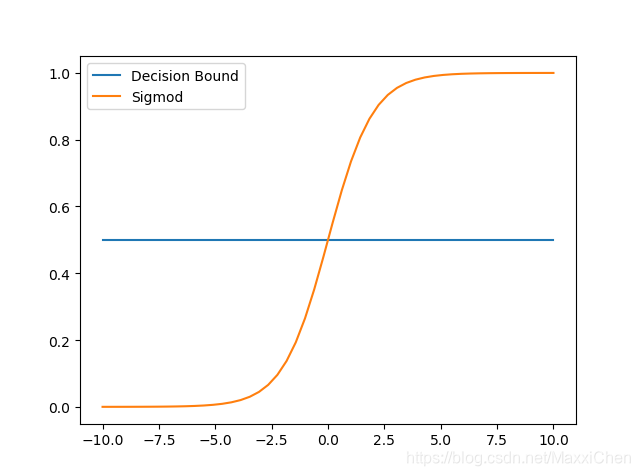
y(z)<0.5 则预测当前数据属于0即未通过考试；
y(z)>0.5 则预测当前数据属于1即通过考试。
所以我们可以将sigmoid函数看成样本数据的概率密度函数。
需要注意的是，这里Sigmod函数建立的前提是：z的分布已知，已知z=b+wx，其中未知数b决定了判断及格的边界（学多长时间有一半几率及格），未知数w决定了学习时间转化为知识掌握程度的效率（每学单位时间，知识掌握能力的提升量）。而相应的两个限制条件为：
1.z=0时为边界
2.在训练集上准确率最优（何为最优？==》在损失函数上取值最小）
于是自然而然引出了损失函数的定义。

损失函数

定义

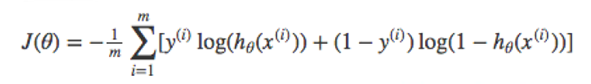
其中m为学生总数，y⁽ⁱ⁾=h_Theta(x⁽ⁱ⁾)为每个学生的及格率

推导

关于同一组事件x⁽¹⁾，x⁽²⁾…的两个分布p，q，其交叉熵(Cross-Entropy)的定义如下：
$$H(p,q)=-\sum _{i=1}^n{p}_{i}log{q}_i$$
当两个分布完全相同时，交叉熵取最小值。
交叉熵可以衡量两个分布之间的相似度，交叉熵越小两个分布越相似。
例如算法判定一个学生100%通过考试(1,0)，他也确实通过了考试，算法的损失（即交叉熵）就为0，当它判定另一个学生100%通过考试(1,0)，该学生却并未及格，则算法完全错误，其损失（即交叉熵）用无限大表示。
于是有：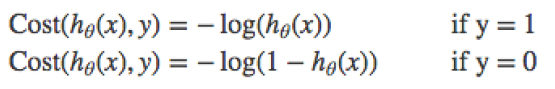

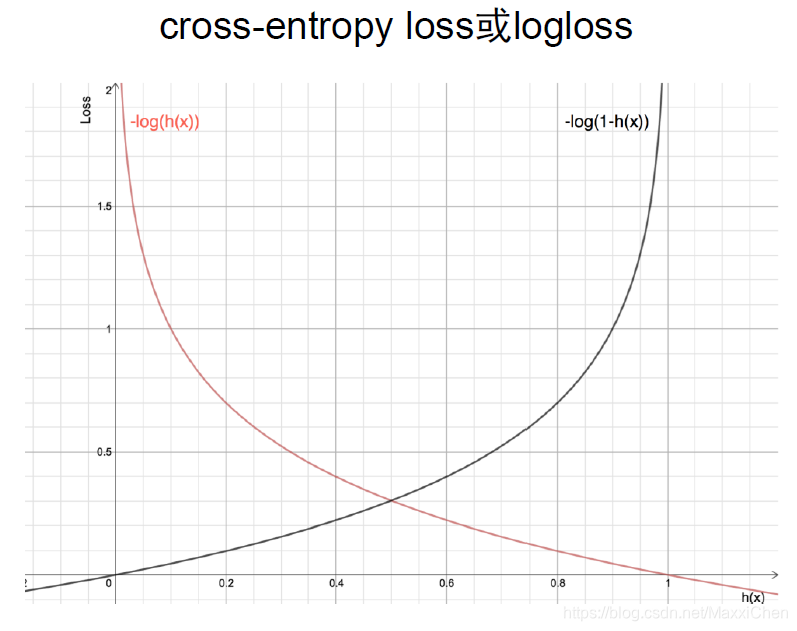
此时预测第三个学生90%几率通过考试10%几率不通过(0.9,0.1)，则此预测中包含的损失为样本标签为1时10%预测为没通过+样本标签为0时90%预测为通过，两种情况发生几率为90%和10%
于是我们可以得出对于每个学生的预测损失为
90% * -log90% + 10% * -log(1-90%)
全体样本损失即

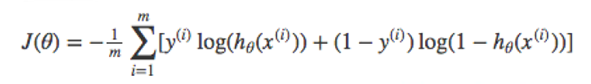
参数更新

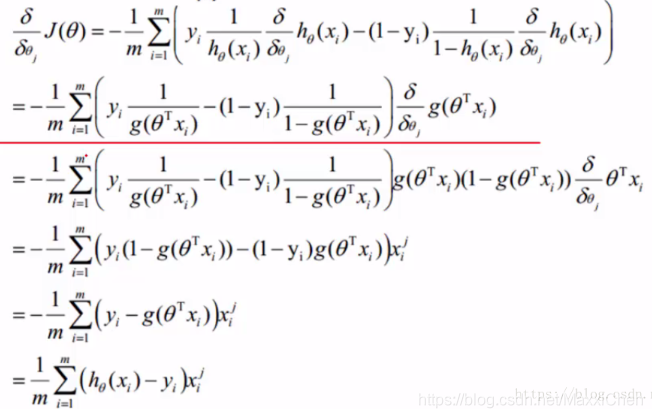
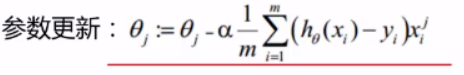
总结

最后获得的theta便精确定义了z(x), 所以逻辑回归和线性回归归根结底是一个东西，都是求出最佳的theta来拟合我们所有的数据，逻辑回归只是在线性回归的基础上再套了一层Sigmod函数，这就是为什么逻辑回归归属于线性回归的package中。

参考:https://blog.youkuaiyun.com/qq_21840201/article/details/81201131

多分类问题

有空再写…