一文看懂简单线性回归：梯度下降法和最小二乘法（代码实现及数学公式详解）

作为监督学习必掌握的模型之一，简单线性回归虽名为简单，但其中也涵盖了诸多数学知识点（例如矩阵计算，向量偏导），虽然很多公式已经集成在了各种package中，但这些知识点的理解掌握对于代码的快速实现以及基础知识的巩固还是大有裨益的。

问题引入

已知一个样本数量为10，带有噪声的一维特征的线性数据集，其Target与Feature的函数关系如图表示为：

现在我们得知一个新的数据feature value(x)=1.5，但其target value未知，如何才能根据现有的样本，最好的去预测其应有的目标值呢？最好的方法就是去拟合一条直线，让它最大程度的代表此样本集的线性关系。当我们求解出了所要的线性模型，再将特征值代入，就能得到最合理的目标值了。
而这个过程就是线性回归。

简单线性回归

一元线性回归

假设数据满足线性模型条件，因此其预测目标值y与特征值x存在关系：
$$y_{pred}=b+wx$$
变化为向量形式为
$$Y_{pred}=\left(\begin{array}{c}{y}_{pred1}\\ y_{pred2}\\ ⋮\end{array}\right)=\left(\begin{array}{cc}1& x_1\\ 1& x_2\\ ⋮& ⋮\end{array}\right)\left(\begin{array}{c}b\\ w\end{array}\right)=X^T\Theta$$
其中b为y轴截距，w为系数。
思路：找到最优的(b,w)使线性模型在历史数据上的误差最小
这里误差的定义为：Sum of Squared Error(SSE)
$$SSE=\sum _{k=0}^{n-1}(y_{predk}-y_k{)}^2=(Y_{pred}-Y{)}^T(Y_{pred}-Y)=(X^T\Theta -Y{)}^T(X^T\Theta -Y)$$

多元线性回归

类比于一元线性回归，数据预测目标值y与特征值x1，x2，…存在关系
$$y_{pred}=b+w_1{x}_1+w_2{x}_2+...+w_m{x}_m$$
变化为向量形式为
$$Y_{pred}=\left(\begin{array}{c}{y}_{pred1}\\ y_{pred2}\\ ⋮\end{array}\right)=\left(\begin{array}{cccc}1& x_{11}& \cdots & x_{m1}\\ 1& x_{12}& \cdots & x_{m2}\\ ⋮& ⋮& \ddots & \\ 1& x_{1n}& \cdots & x_{mn}\end{array}\right)\left(\begin{array}{c}b\\ W\end{array}\right)=X^T\Theta$$
$$\begin{gathered} SSE=\sum _{k=0}^{n-1}(y_{predk}-y_k{)}^2 \\ =(Y_{pred}-Y{)}^T(Y_{pred}-Y) \\ =(X^T\Theta -Y{)}^T(X^T\Theta -Y) \end{gathered}$$

梯度下降法

关于梯度下降算法的直观理解，我们以一个人下山为例。比如刚开始的初始位置是在黄色山顶位置，那么现在的问题是该如何达到蓝色的山底呢？按照梯度下降算法的思想，它将按如下操作达到最低点：

第一步，明确自己现在所处的位置

第二步，找到相对于该位置而言下降最快的方向

第三步， 沿着第二步找到的方向走一小步，到达一个新的位置，此时的位置肯定比原来低

第四部， 回到第一步

第五步，终止于最低点



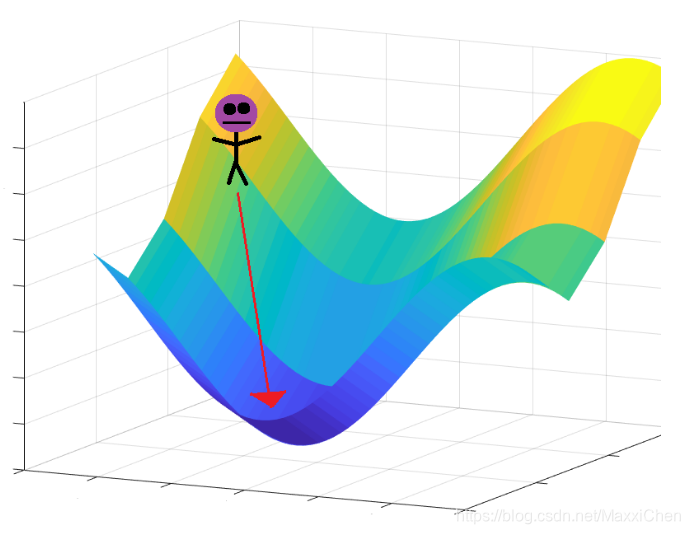
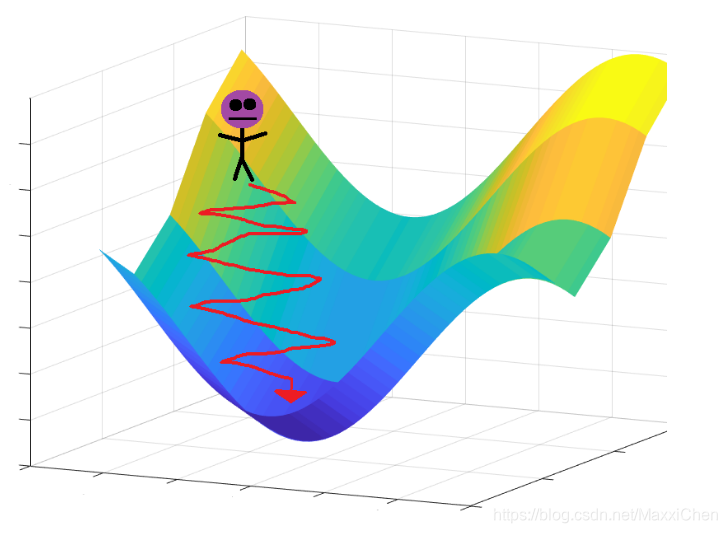
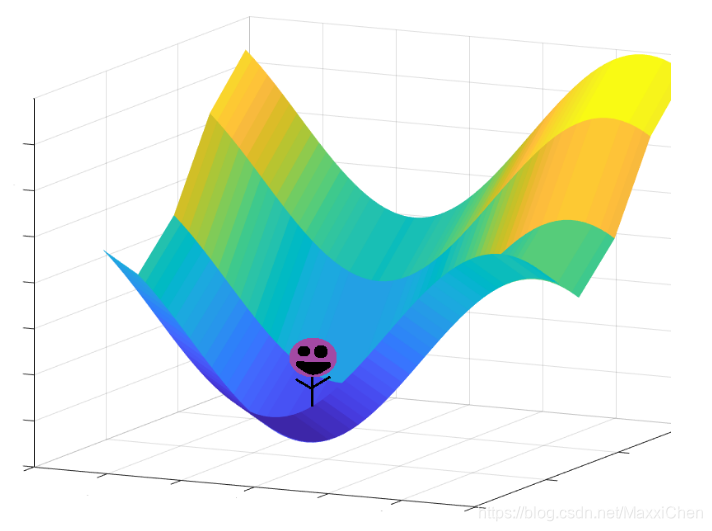
而在线性回归问题中，山的高度其实就是我们的SSE损失函数，平面的两个维度就是我们的b和w即theta，已知theta，就能得知我们的海拔高度。而当前位置降速最大的方向就可以用当前位置的梯度来表示
$$\nabla (SSE(\Theta ))=X(Y_{pred}-Y)$$
通过超参数：步长学习率alpha来限制我们的迭代速度
$${\Theta }^{{}^{\prime }}=\Theta -\alpha \nabla (SSE(\Theta ))$$
结束条件即是到达谷底或到达最大迭代次数。
这个方法求解的是近似值适合数据量较大，在最小二乘法因而效率不高时使用。

最小二乘法

相比于盲人摸象的梯度下降法，如果我们在山顶能够眺望，就可以一步到位找到谷底所在位置。如果说梯度下降是我们的双腿那最小二乘法就类似于我们的眼睛。
由于我们可以得到ESS的完整表达，那么山底的位置即是其对theta一次求导为零的地，表达为：
$$\nabla (SSE(\Theta ))=(X{X}^T+X^{T}X)\Theta -XY-XY=0$$
其含义即是Least Sum of Squares
得到：
$$\Theta =(X{X}^T{)}^{-1}XY$$
而theta即包含了线性模型所需的条件。
这个方法求解的是精确解适合数据量较小，由于在最小二乘法中需要用到矩阵的逆，对逆的求解会占用大量内存，因而对于数据量庞大的情况并不理想。

代码实现

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import numpy as np

def grad_descent(X, Y, alpha=0.01, iter_max=500):
    """
        针对简单线性回归的梯度下降算法
        Parameters
        ----------
        X :         特征矩阵
                    shape为(n_features+1,n_samples)的齐次坐标
        y :         标签向量
                    shape为(n_samples,1)
        alpha :     学习步长
                    optinal，default=0.01
        iter_max :  最大迭代次数
                    optional，default=500
    
        Returns
        -------
        Theta :     (w,b)
                    其中w为coefficient，b为interception
    """
    Theta = np.array([np.random.randn(2)]).reshape(-1,1)
    tolerance = 1e-3
    iterations = 1
    bool_conv = False# loop condition
    m = len(Y)# n_samples       
    
    while not bool_conv:
        Y_p = X.T.dot(Theta)#predicted Y
        Error = Y_p-Y
        Gradient = X.dot(Error)
        cost = 1 / (2 * m) * np.sum(Error ** 2)
        Theta = Theta - alpha * Gradient
        iterations += 1
        
        if np.sum(alpha * np.linalg.norm(Gradient,ord=2)) < tolerance:
            bool_conv = True
            print('Theta收敛')
        if iterations % 10 == 0:
            print('第{}次迭代，cost {:.4f}'.format(iterations, cost))
        if iterations > iter_max:
            bool_conv = True
            print('已至最大迭代次数{}，运算结束'.format(iter_max))
    
    return Theta

# 生产一元随机回归数据集
X,Y = make_regression(n_samples=10,n_features=1,n_informative=1,\
                      n_targets=1,noise=50,random_state=0)
# 数据分割
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=1/4,\
                                random_state=0)
# 梯度下降法=============================================================================
#数据整理
X = X.reshape(-1)
X = np.vstack((np.ones_like(X),X))
Y = Y.reshape(len(Y),1)
Theta = grad_descent(X, Y, alpha=0.01, iter_max=1500)

# 拟合可视化
plt.figure()
plt.title('Linear Regression with 1 Feature')
ax1 = plt.scatter(X[1], Y, marker= 'o', s=50)
plt.plot(X[1],X[1]*Theta[1]+Theta[0],'r', label='Gradient Descending')
plt.xlabel('Feature_value(x)')
plt.ylabel('Target_value(y)')  
# 最小二乘法=============================================================================
# 建立回归模型
linreg = LinearRegression().fit(X_train,Y_train)
print('模型系数w：{}\n模型截距b：{}\n训练集R^2得分：{}\n测试集R^2得分：{:.3f}'\
      .format(linreg.coef_, linreg.intercept_,linreg.score(X_train,Y_train)\
      ,linreg.score(X_test,Y_test)))
# 回归拟合
ax2 = plt.plot(X[1],X[1]*linreg.coef_+linreg.intercept_,'g',label='Least Sum of Squares')
plt.legend()

绘图结果