暴力/蛮力法经典例题--求解迷宫问题--C语言

最新推荐文章于 2022-07-14 13:51:01 发布
原创 最新推荐文章于 2022-07-14 13:51:01 发布 · 597 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#c语言 #算法 #深度优先

问题描述：

        有如下5*5的迷宫，其中数字0代表通路方块，1代表障碍方块，设迷宫入口为（0，0），出口为（4，4），设计程序找到所有可能的逃脱路线。

                                     

 

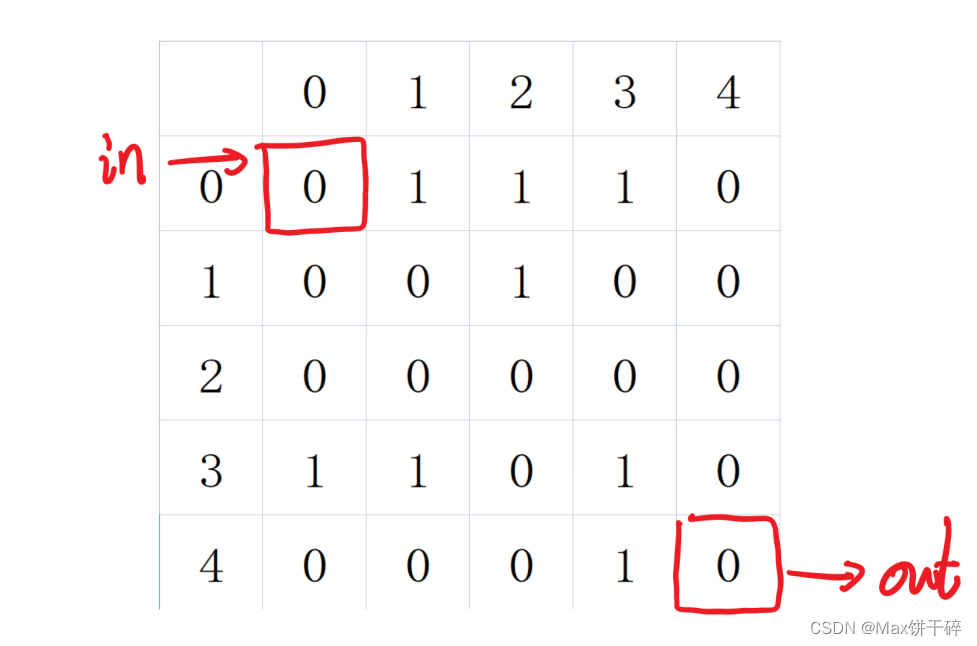
思路：

        题目与图的邻接矩阵的深搜或者广搜基本一致，这里我介绍下深搜。

        这里我们把迷宫其中一个小方格拿出来看。

        我们可以看到，对于每一个小方格，下一步的走法只有四种选择，上下左右，并且只能走值为0的格子，且不能越界。

                                  

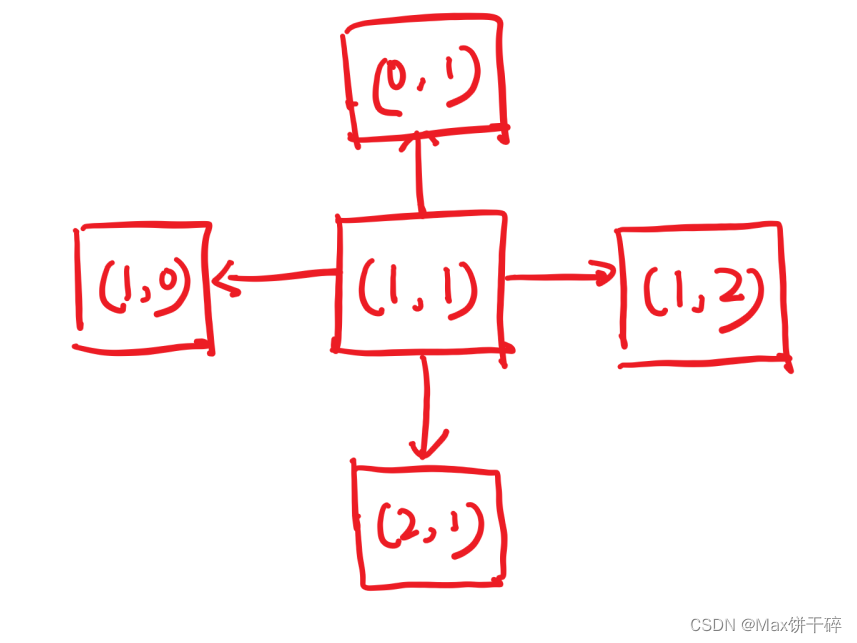
         那么我们就可以仅考虑出口以及第一个小个子的走法，剩下

最低0.47元/天 解锁文章
C语言蛮力法解决迷宫问题
小林先生的博客
10-18 451
//迷宫问题解法2 #include <stdio.h> #define MAXQ 100 //队列大小 #define MAxN 10 //最大迷宫大小 //问题表示 int n=8; char Maze[MAxN][MAxN]={ //迷宫大小 {‘O’,‘x’,‘x’,‘x’,‘x’,‘x’,‘x’,‘x’}, {‘O’,‘O’,‘O’,...
暴力/蛮力法经典例题--求解任务分配问题--C语言
MaxDeCookies的博客
06-30 2025
问题描述： 有n（>=1）个任务需要分配给n个人执行，每个任务职能分配给一个人，每个人只能执行一个任务，每个人完成各个任务对应的消耗如下表，求最小的分配方案。 ...
C语言实现，找出迷宫起点到终点的最短路径，最详细的DFS教程
s_meng_的博客
05-02 4286
因为蓝桥杯要去参加国赛了，现在要开始备考了，下午学了下DFS的算法，然后输出一下我学到的。 求出迷宫中的最短路径: 一共有两个，一个是未改进的，但是更容易理解，理解了第一个之后，可以更好的理解第二个优化的。 尝试移动的方向，当开始移动时，坐标的变化。 未优化 /* 输入m行,n列数据, p,q表示终点, min表示最短路径 */ int m, n, p, q; int min = 999999999; int a[100][100]; //1表示空,2表示障碍 int v[100][100]; //
蛮力法例题
lsj的博客
05-16 848
算法设计与分析--蛮力法例题
暴力/蛮力法经典例题--全部幂集问题--C语言
MaxDeCookies的博客
06-29 752
问题描述： 给定正整数n大于等于1，求1~n构成的所有集合，包括空集。
蛮力算法 例题
@@老胡的博客
03-22 1237
这个算法比较简单 给你一个数组 prices ，其中 prices[i] 是商店里第 i 件商品的价格。 商店里正在进行促销活动，如果你要买第 i 件商品，那么你可以得到与 prices[j] 相等的折扣，其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ，如果没有满足条件的 j ，你将没有任何折扣。 请你返回一个数组，数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。 示例 1： 输入：prices = [8,4,6,2,3] 输出：
蛮力枚举算法C语言,算法01-蛮力法
weixin_39626089的博客
05-24 925
算法01-蛮力法一、蛮力法介绍蛮力法(brute force method，也称为穷举法或枚举法)是一种简单直接地解决问题的方法，常常直接基于问题的描述，所以，蛮力法也是最容易应用的方法。但是，用蛮力法设计的算法时间特性往往也是最低的，典型的指数时间算法一般都是通过蛮力搜索而得到的 。常见的蛮力法：冒泡排序、选择排序。二、冒泡排序1、基本思想冒泡排序(Bubble Sort)，是一种计算机科学领域...
暴力/蛮力法经典例题--0/1背包问题--C语言
MaxDeCookies的博客
06-29 2862
问题描述： 有n个重量各不相同的物品（物品编号为0~n-1），他们的价值也各不相同，给定一个容量为mw=6的背包，问在能装人背包的物品组合中，最大的价值为多少。
回溯法经典例题--0/1背包问题--C语言
MaxDeCookies的博客
07-05 2520
问题描述： 设n个物品的编号为0~n-1，重量和价值分别用数组w【】与v【】存放，背包限制重量用W表示，X【】存放最优解，x【i】的值为0、1分别表示物品i不在、在背包内。
c语言--分治法经典例题--求解棋盘覆盖问题
MaxDeCookies的博客
06-27 2188
有关分支经典问题期盼填充问题的一个解法
蛮力法 算法设计实验程序C语言编写
11-30
蛮力法解最近对 凸包 字符串匹配 自己写的有不足之处还请指教
求解迷宫全部路径问题
10-07
问题描述： 以一个m*n的长方阵表示迷宫，0和1分别表示迷宫中的通路和障碍。设计一个程序，对任意设定的迷宫，求出从入口（0，0）到出口（m-1，n-1）的通路和通路总数，或得出没有通路的结论。例如下图， 0（入口） 1 0 1 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0（出口） 从入口到出口有6条不同的通路。 而下图： 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 0 0 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 0 0 从入口到出口则没有通路。 算法设计： 给定一个m*n的长方阵表示迷宫，设计算法输出入口到出口的通路和通路总数，或得出没有通路的结论。 算法提示： 和皇后问题与分书问题类似。可以用二维数组存储迷宫数据，对于迷宫中任一位置，均可约定有东、南、西、北四个方向可通。从当前位置a（用（x，y）表示一个位置，假定它是以向右的x轴和向下的y轴组成的平面上的一个点）出发依次尝试四个方向是否有路，若某个方向的位置b可通，则按照同样的方法继续从b出发寻找。若到达出口，则找到一条通路。 数据输入： 由文件input.txt 提供输入数据。第一行是m和n的值，空格分隔，其后共m行。每行有n个数字，数和数之间用空格分隔。 结果输出： 将计算出的所有从入口到出口的通路输出到文件output.txt 中。若没有通路，则将0写入文件中。
c语言迷宫问题，暴力算法直接遍历
07-27
c语言迷宫问题，暴力算法直接遍历
C语言--分治法经典例题--循环日程安排问题
MaxDeCookies的博客
06-28 3132
问题描述： 有size=2^n个选手要进行网球循环赛，设计一个满足以下要求的比赛日程表。
蛮力算法解决问题（c语言）
呼啦啦啦啦啦的博客
07-14 1138
蛮力算法解决问题（c语言）
暴力/蛮力法经典例题--最大连续子序列和--C语言
MaxDeCookies的博客
06-29 1426
给定一串n个整数的序列，从中找出最大连续子序列的和，结果最小不能低于0，若小于0则直接返回0。
c++蛮力法例子_算法总结-回溯法
weixin_36485321的博客
12-05 800
回溯法是一种通过暴力穷举的方式解决问题的方式，是深度优先搜索的一种具体应用。其思路不难理解，想象一下你在走一个迷宫，当在一个路口有A， B， C 三条岔路的时候你要怎么办呢？ 大家可以很容易地想到先尝试道路A， 如果走不通就回到这个路口尝试道路B，如果还走不通就尝试道路C，这就是一个典型地应用回溯法的例子。如果将目光着眼于整个迷宫，就可以发现这个迷宫其实就是一颗多叉树，每个路口就是一个节点，每个路...
二维数组迷宫求解c语言,c语言写的迷宫问题
weixin_30738065的博客
05-21 401
该楼层疑似违规已被系统折叠隐藏此楼查看此楼下面是程序#include#define OVERFLOW -2#define ERROR 0#define NULL 0#define true 1#define TRUE 1#define false 0#define FALSE 0#define STACK_INIT_SIZE 100#define STACKINCREMENT 10#includ...
Easyx图形库小游戏---迷宫
deroy
10-25 4608
迷宫迷宫生成十字分割方法生成DFS 方法生成：实战演练十字分割DFS 方法 来源：微信公众号「编程学习基地」 源码获取关注微信公众号，发送关键字 迷宫生成 ​ ① 十字分割 递归版本 ​ ② BFS（即广度算法） 十字分割方法生成 ​ 要求初始时迷宫内全是通路，然后随机十字建墙，然后随机在三面墙上打洞，使四个子空间连通。 ​ 要求：十字点横纵坐标均要求为偶数（即地图行列为奇数），打洞点要求为奇数。 DFS 方法生成： ​ 像一只地鼠打洞一般，迷宫要求初始时全是阻碍（墙），然后随
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值