本文介绍了一个用L型骨牌覆盖2^k*2^k正方形棋盘的算法，其中特殊方格除外。通过分治策略，将棋盘分为四个区域，并根据特殊方格位置填充对应区域的对角方格，递归执行直至只剩一个方格。在递归过程中，当棋盘大小为1时直接返回，因为填充已在之前的条件分支中完成。核心代码展示了如何根据四个区域的位置关系进行递归处理。
问题描述：
有一个2^k*2^k的正方形棋盘，在其内部有一个特殊方格标记为0，现在要用L形状的骨牌来覆盖除了特殊方格外的全部期盼，骨牌可以任意旋转但不能重叠。
求解：
基本思想利用分治把棋盘等分为四块，利用每一块的左上角坐标（tx，ty）与特殊方块坐标（x，y）来进行判断，假如特殊方块在左上的区域内，就填充属于其他三个区域最对角的方块，如左上就填充这个区域的最有下的方块，左下就填充这个区域的最右上方块，看图好理解些。
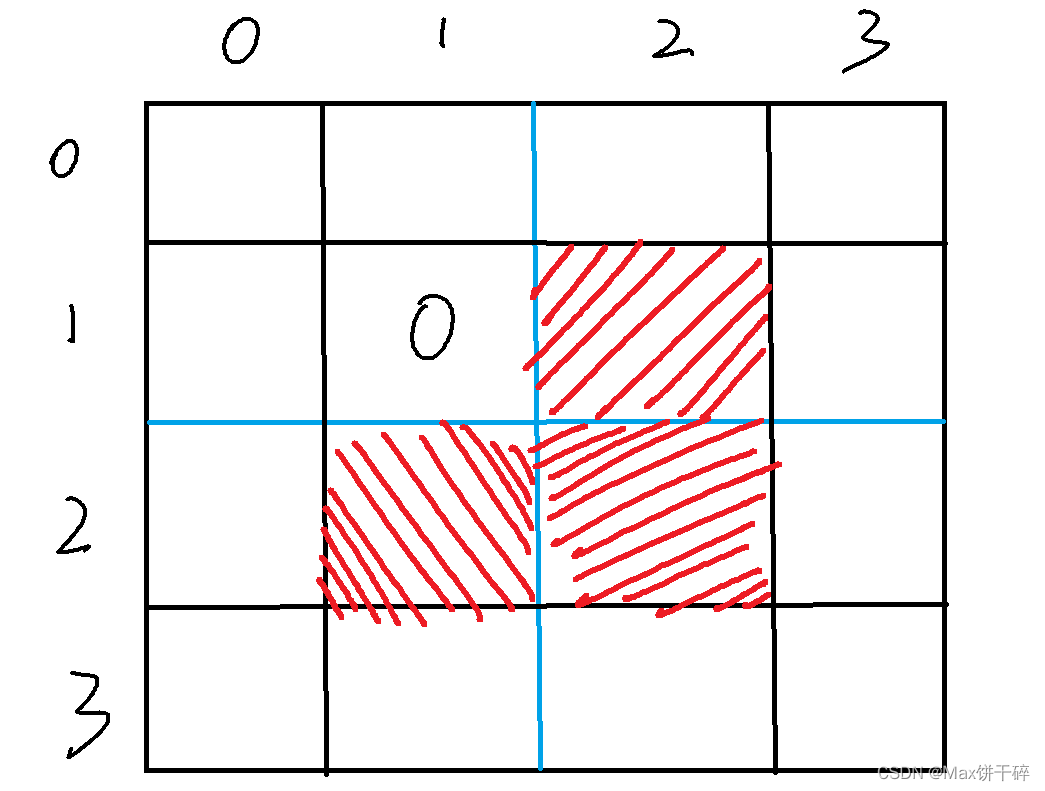
其实这三个区域的填充部分就是为了将红色区域充当每个区域的特殊方块，好让各自递归的执行下去（所谓的没有条件也要创造条件上：）），当执行到size==1（size为边长）时因就剩一个方格就不需要进行操作，可以直接return了。
这里为什么size==1就直接返回而不是进行填充，是因为填充的这一步操作在每一个if-else的else里面已经执行了，第一句就是。
number的值是用来充当不同的L型骨牌.
这里的method方法就是主要的代码，因为依次检查四个区域属于重复性操作，所以这里就解释第一个if—else。
if (x < tx + size 
最低0.47元/天 解锁文章
扫一扫
3106
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
