【多旅行商问题】基于多目标蛇优化算法MOSO求解多旅行商问题MTSP（旅行商个数和起点城市可修改）研究（Matlab代码实现）

最新推荐文章于 2025-12-04 22:00:44 发布
原创 最新推荐文章于 2025-12-04 22:00:44 发布 · 772 阅读 · 29 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #matlab #开发语言 #支持向量机

   💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于多目标蛇优化算法MOSO求解多旅行商问题MTSP（旅行商个数和起点城市可修改）研究

一、引言

多旅行商问题（Multiple Traveling Salesman Problem, MTSP）是经典的旅行商问题（Traveling Salesman Problem, TSP）的扩展，在物流配送、网络路由、电路设计等多个工程领域具有广泛的应用。MTSP的核心目标是为多个旅行商规划访问一系列城市的最优路径，使得所有城市都被访问一次且仅一次，并最终返回起点，通常以最小化总路径距离或总成本等为目标。随着问题规模的增大，MTSP的求解难度呈指数级增长，传统的精确算法难以在合理时间内获得最优解，因此启发式算法和元启发式算法成为解决MTSP的主要手段。

多目标蛇优化算法（Multiple Objective Snake Optimizer, MOSO）是一种基于群体智能的元启发式优化算法，它模拟了蛇的觅食和繁殖行为，具有较强的全局搜索能力和自适应收敛特性。将MOSO应用于MTSP的求解，有望在合理的时间内获得高质量的解，满足实际应用的需求。本研究的重点在于利用MOSO求解MTSP，并允许用户灵活修改旅行商个数和起点城市，以适应不同的应用场景。

二、多旅行商问题MTSP的数学模型

2.1 问题定义

给定一个包含n座城市的城市集合V={0,1,…,n}，其中城市0为起点（仓库）。指定m个推销员（旅行商），每个推销员从起点城市出发，访问一定数量的城市，最后回到起点城市。要求除起点城市以外，每一座城市都必须至少被一位推销员访问，并且只能访问一次。

2.2 双目标数学模型

本研究采用双目标优化模型，目标函数分别为所有推销员的总路程f1​和推销员中最长路线与最短路线的差值f2​（即平衡度）。数学模型表述如下：

2.3 约束条件

三、多目标蛇优化算法MOSO

3.1 算法背景

蛇优化算法（Snake Optimizer, SO）由Fatma A. Hussien于2022年提出，该算法模拟了蛇的觅食和繁殖行为。多目标蛇优化算法MOSO是在SO的基础上，结合多目标优化思想形成的，旨在解决多目标优化问题。MOSO将群体分成雄性和雌性两个相等的群体，通过模拟蛇在不同环境条件下的行为，实现全局探索和局部开发，从而在解空间中搜索最优解。

3.2 算法流程

MOSO的优化过程分为探索和开发两个阶段，根据温度和食物数量的变化，进一步细分为三个阶段：捕食阶段、战斗阶段和交配阶段。

3.2.1 初始化阶段
  • 设置算法参数，包括种群大小Np​、外部存档大小Nr​、最大迭代次数maxgen、网格数量ngrid、最大速度maxvel等。
  • 随机生成初始种群，每个个体代表一个可能的解，即MTSP的一种路径分配方案。
3.2.2 捕食阶段（全局探索）

  • 如果温度T低且食物充足（Q<0.25），蛇通过选择任何随机位置来搜索食物，并更新它们的位置。雄性蛇和雌性蛇的位置更新方式类似，但具体参数可能有所不同。

  • 例如，雄性蛇的位置更新公式可能为：

3.2.3 战斗阶段（竞争与选择）
  • 如果温度T高且食物充足（Q>0.25且T>0.6），蛇将处于战斗模式。雄性蛇之间为了争夺最佳雌性而战斗，每个雌性也会尝试选择最好的雄性。
  • 在战斗过程中，根据个体的适应度值进行竞争，适应度高的个体有更大的机会生存下来并传递其基因。
3.2.4 交配阶段（局部开发）
  • 如果温度T低且食物充足（Q>0.25且T<0.6），蛇将处于交配模式。每对配对之间发生交配，与食物数量的可用性有关。
  • 交配过程中，通过交叉和变异操作产生新的子代个体。交叉操作可以借鉴遗传算法中的交叉策略，如顺序交叉（OX）或部分映射交叉（PMX）；变异操作可以采用交换变异、逆转变异等方式。
3.2.5 环境选择阶段
  • 利用环境选择算子对子代进行筛选，以便进行下一轮迭代。环境选择算子主要用于选择精英个体，这些个体能够支配种群中的其他个体或者互相不支配。
  • 直到满足算法的终止条件（如达到最大迭代次数），最后一次环境选择出来的所有个体即为最终的近似Pareto解集。

3.3 性能评价指标

为了评估MOSO算法求解MTSP的性能，采用六种性能评价指标：

  • Generational Distance (GD)：衡量算法生成的非支配解集与真实帕累托前沿之间距离的指标。GD值越小，表示算法的收敛性越好，即解集越接近真实帕累托前沿。
  • Inverted Generational Distance (IGD)：同时考虑了算法的收敛性和多样性。IGD值越小，表示算法的性能越好，即解集在多样性和收敛性上都更接近真实帕累托前沿。
  • Hypervolume (HV)：衡量目标空间被非支配解集覆盖的程度。它需要一个参考点，通常是各个目标上的最大值形成的向量。HV值越大，表示算法的收敛性和多样性越好。
  • Spacing：衡量解集中各个解之间分布均匀性的指标。Spacing值越小，说明解集的分布越均匀。
  • Spread：衡量解集在目标空间中的分布范围。Spread值越大，表示解集的分布范围越广。
  • Coverage：用于衡量一个解集对另一个解集的覆盖能力。如果解集A的Coverage指标高于解集B，那么意味着解集A在某种程度上能够被解集B覆盖。

四、MOSO求解MTSP的实现

4.1 问题编码

在MOSO中，采用基于路径的编码方式来表示MTSP的解。每个个体（蛇）的位置向量包含所有旅行商的路径信息。例如，对于m个旅行商和n个城市（不包括起点城市0），个体位置向量的长度为n+m−1。其中，前n个元素表示城市的访问顺序，后m−1个元素用于分隔不同旅行商的路径。

4.2 适应度函数设计

适应度函数用于评估个体的优劣，指导算法的搜索方向。对于MTSP的双目标优化问题，采用加权求和的方法将双目标转化为单目标进行评估。具体公式如下：

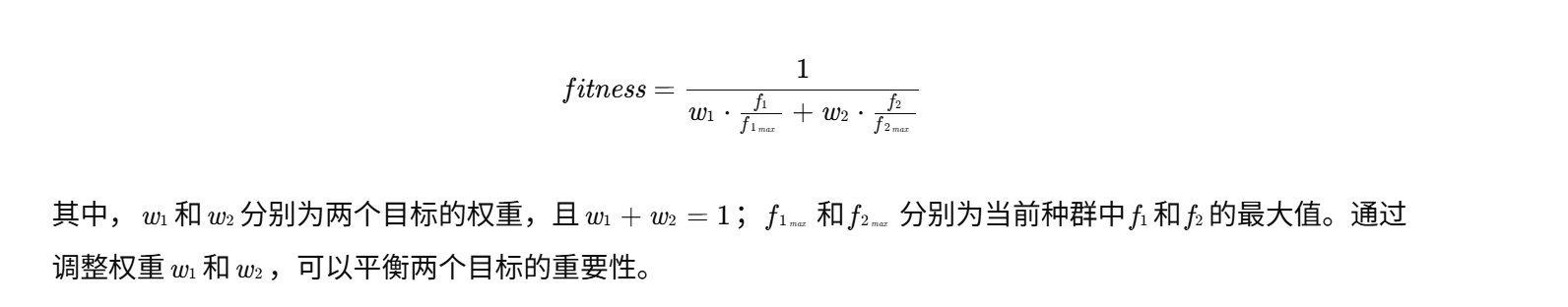
4.3 MATLAB代码实现

以下是基于MOSO求解MTSP的MATLAB代码框架：

matlab

% 参数设置
Tnum = 5; % 旅行商个数（可以自行更改）
StartPoint = 1; % 选择起点城市（可以自行更改）
params.Np = 100; % 种群大小
params.Nr = 200; % 外部存档大小
params.maxgen = 100; % 最大迭代次数
params.ngrid = 30; % 网格数量
params.maxvel = 5; % 最大速度
% 加载城市坐标数据（以TSPLIB中的bayg29为例）
load('bayg29_data.mat'); % 假设数据文件中包含城市坐标矩阵coordinates
n = size(coordinates, 1); % 城市数量
% 计算距离矩阵
distanceMatrix = zeros(n, n);
for i = 1:n
for j = 1:n
distanceMatrix(i, j) = norm(coordinates(i, :) - coordinates(j, :));
end
end
% 定义目标函数
MultiObjFnc = @(x) calculateObjectives(x, distanceMatrix, Tnum, StartPoint);
% 运行MOSO算法
REP = MOSO(params, MultiObjFnc);
% 获取Pareto前沿和路径规划结果
Obtained_Pareto = REP.pos_fit;
X = REP.pos;
% 绘制Pareto前沿
if size(Obtained_Pareto, 2) == 2
figure;
plot(Obtained_Pareto(:, 1), Obtained_Pareto(:, 2), 'ok');
xlabel('f1 (Total Distance)');
ylabel('f2 (Balance Degree)');
title('Pareto Front obtained by MOSO');
grid on;
end
% 目标函数计算函数
function [f1, f2] = calculateObjectives(x, distanceMatrix, Tnum, StartPoint)
% 解码路径
paths = decodePath(x, Tnum, StartPoint);
% 计算每个旅行商的路径长度
travelerDistances = zeros(Tnum, 1);
for k = 1:Tnum
path = paths{k};
distance = 0;
for i = 1:length(path) - 1
distance = distance + distanceMatrix(path(i), path(i + 1));
end
travelerDistances(k) = distance;
end
% 计算总路程和平衡度
f1 = sum(travelerDistances);
f2 = max(travelerDistances) - min(travelerDistances);
end
% 路径解码函数
function paths = decodePath(x, Tnum, StartPoint)
% 此处需要根据具体的编码方式进行路径解码
% 以下是一个简单的示例框架，实际实现需要根据编码细节进行调整
n = length(x) - Tnum + 1; % 城市数量（不包括起点）
cityIndices = 1:n;
separators = x(end - Tnum + 2:end); % 分隔符位置（假设后m - 1个元素为分隔符）
% 对分隔符进行排序并调整
[~, sortIdx] = sort(separators);
newSeparators = zeros(Tnum - 1, 1);
for i = 1:Tnum - 1
newSeparators(i) = round((i - 1) * n / (Tnum - 1)); % 简单均匀分隔示例
end
% 实际应用中需要根据分隔符的编码规则进行准确解码
% 分割城市序列为不同旅行商的路径
paths = cell(Tnum, 1);
startIdx = 1;
for k = 1:Tnum - 1
endIdx = newSeparators(k);
path = [StartPoint, cityIndices(startIdx:endIdx), StartPoint];
paths{k} = path;
startIdx = endIdx + 1;
end
paths{Tnum} = [StartPoint, cityIndices(startIdx:end), StartPoint];
end
% MOSO算法主体函数（此处省略具体实现，可参考相关文献或开源代码）
function REP = MOSO(params, MultiObjFnc)
% 初始化种群
% 迭代过程（捕食、战斗、交配、环境选择）
% 返回最终的非支配解集和对应的解
end

4.4 实验结果与分析

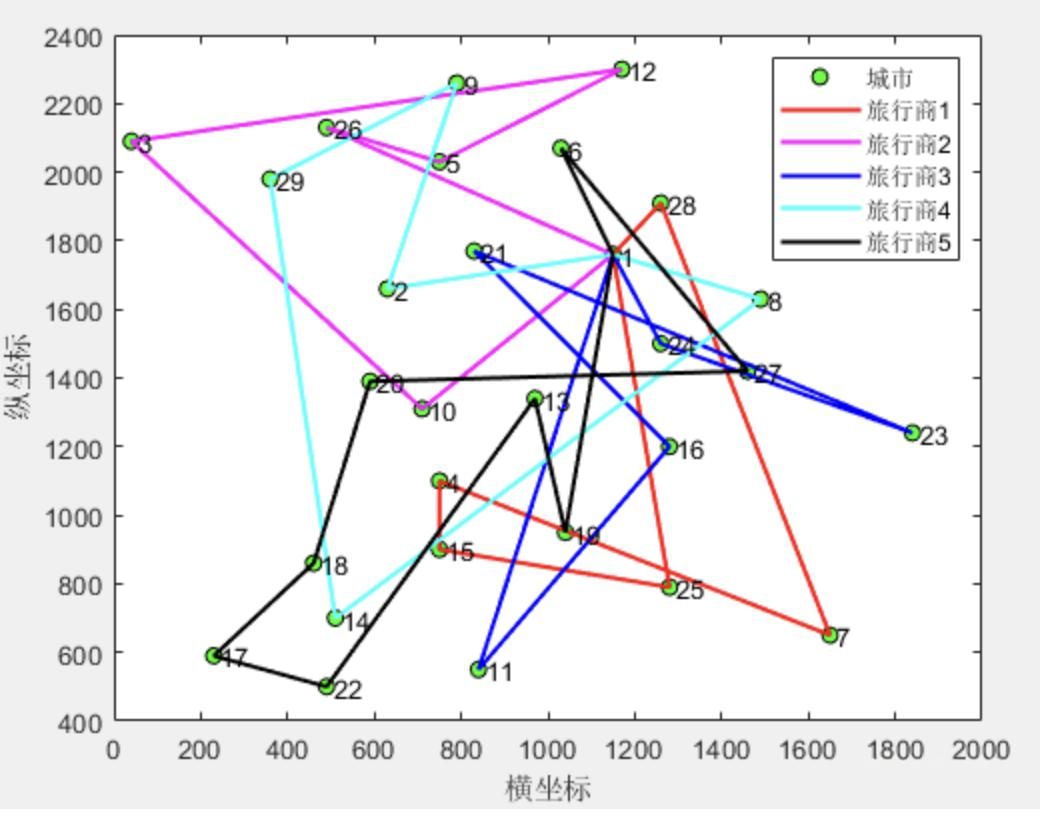
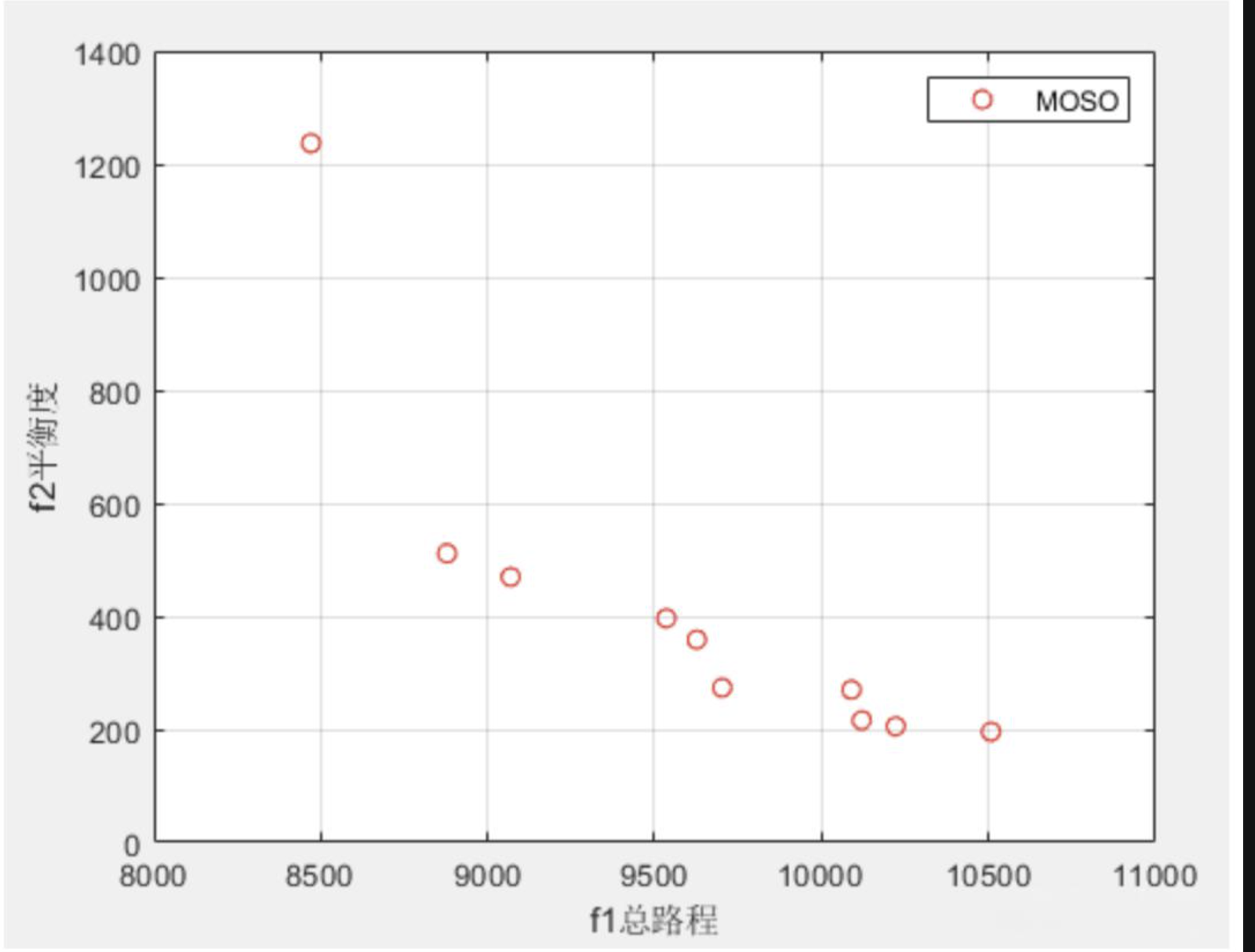
通过在TSPLIB中的bayg29实例上进行实验，调整旅行商数量和起点城市，可以得到不同配置下的Pareto前沿和路径规划结果。实验结果表明，MOSO算法能够有效地求解MTSP，获得一组近似Pareto最优解，满足不同目标的需求。

例如，当设置旅行商数量为5，起点城市为1时，得到的Pareto前沿显示了总路程和平衡度之间的权衡关系。用户可以根据实际需求选择合适的解，如追求最短总路程或更均衡的路径分配。

五、应用场景与优势

5.1 应用场景

  • 物流配送：物流企业从仓库出发，安排多个配送车辆（旅行商）向多个客户点送货。通过MOSO求解MTSP，可以合理规划路线，显著降低运输成本，提高配送效率。
  • 快递服务：快递分拨中心作为仓库，快递员作为旅行商，需要将包裹派送到各个收件地址。优化路线能减少快递员的工作时间和行程，提高快递服务的质量和效率。
  • 移动机器人路径规划：在大型工厂或仓库中，多个移动机器人需要从一个充电点（仓库）出发，完成对不同区域的货物搬运、巡检等任务。通过解决MTSP可以为机器人规划高效的路径，提高生产自动化水平和效率。

5.2 优势

  • 多目标优化能力：MOSO能够同时优化多个目标，如总路程和平衡度，满足不同应用场景的需求。
  • 灵活性：允许用户灵活修改旅行商个数和起点城市，适应不同的实际问题。
  • 全局搜索能力：通过模拟蛇的觅食和繁殖行为，MOSO具有较强的全局搜索能力，能够在解空间中找到高质量的解。
  • 自适应收敛特性：算法根据温度和食物数量的变化自动调整搜索策略，实现自适应收敛，提高求解效率。

六、结论与展望

本研究提出了一种基于多目标蛇优化算法MOSO求解多旅行商问题MTSP的方法，通过数学建模、算法设计和实验验证，证明了该方法的有效性和可行性。实验结果表明，MOSO能够在合理的时间内获得高质量的近似Pareto最优解，满足不同应用场景的需求。

未来的研究可以从以下几个方面展开：

  • 算法改进：进一步优化MOSO算法的参数设置和操作策略，提高算法的收敛速度和求解质量。
  • 与其他算法融合：将MOSO与其他启发式算法或元启发式算法相结合，形成混合算法，充分发挥各算法的优势。
  • 实际应用拓展：将本研究成果应用于更多的实际领域，如电力维修、网络维护等，解决实际问题，验证算法的实用性和鲁棒性。

📚2 运行结果

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取

                                                           在这里插入图片描述

荧光Matlab
关注
多目标应用：多目标蛇优化算法MOSO求解多旅行商问题MTSP（旅行商个数和起点城市可修改）
IT猿手
02-07 894
多旅行商问题（Multiple Traveling Salesman Problem, MTSP）是著名的旅行商问题（Traveling Salesman Problem, TSP）的延伸，多旅行商问题定义为：给定一个𝑛座城市的城市集合，指定𝑚个推销员，每一位推销员从起点城市出发访问一定数量的城市，最后回到终点城市，要求除起点和终点城市以外，每一座城市都必须至少被一位推销员访问，并且只能访问一次，需要求解出满足上述要求并且代价最小的分配方案，其中的代价通常用总路程长度来代替，当然也可以是时间、费用等
【多旅行商问题】基于多目标蛇优化算法MOSO求解多旅行商问题MTSP（旅行商个数和起点城市可修改）研究附Matlab代码
Matlab_jiqi的博客
11-14 569
一、引言在物流配送、路径规划、电路设计等众多实际领域，常常会遇到需要多个旅行商共同完成对所有城市的遍历，且要满足多种优化目标的问题，这就是多旅行商问题（Multiple Traveling Salesman Problem, MTSP）。传统的单目标优化算法在处理此类多目标问题时，往往难以同时兼顾多个目标的最优解，而多目标优化算法能够提供一组 Pareto 最优解，为决策者提供更多的选择。
【多旅行商问题】基于多目标蛇优化算法MOSO求解多旅行商问题MTSP（旅行商个数和起点城市可修改）研究附Matlab代码.rar
10-15
多旅行商问题（Multiple Traveling Salesman Problem, MTSP）是组合优化领域的一个经典问题，涉及到多个旅行商同时从各自的城市出发，最终返回起点的同时访问所有城市各一次的问题。MTSP在现实生活中具有广泛的应用...
“多目标白鲸与蛇优化算法在MATLAB中的实践与应用：测试报告与源码分享”
08-02
文中详细描述了将蛇优化算法的优良策略与多目标优化算法框架（网格法）结合形成的多目标蛇优化算法（MOSO），并在ZDT系列、Kursawe、Poloni、Viennet2和Viennet3等多个经典测试函数上进行了实验。实验结果表明，这两...
电机结构优化中多目标粒子群算法(MOSO)的MATLAB实现及应用
07-28
利用多目标粒子群算法（MOSO）对电机结构进行优化的方法及其MATLAB实现。文章首先概述了MOSO算法的基本原理，接着展示了如何通过构建代价函数并将其应用于电机结构优化的具体步骤。文中提供了详细的代码示例，包括...
多目标白鲸优化算法MOBWO在Matlab环境下的实证研究及其应用
05-31
文中详细描述了将蛇优化算法的优良策略与多目标优化算法框架（网格法）结合形成的多目标蛇优化算法（MOSO），并在ZDT系列、Kursawe、Poloni、Viennet2和Viennet3等多个经典测试函数上进行了实验。实验结果表明，这两...
电机结构优化中多目标粒子群算法的MATLAB实现与应用 - Pareto前沿 指南
08-27
内容概要：本文介绍了基于多目标粒子群算法（MOSO）的电机结构优化方法，提供了完整的MATLAB代码实现框架，包括代价函数构建、粒子群初始化、迭代更新策略及全局最优解选择机制。文中详细说明了算法核心模块的设计...
欧几里得距离算法-相似度
weixin_45609702的博客
12-04 146
本文介绍了一个计算欧几里得距离的Java方法。该方法接收两个Double数组作为输入，通过计算对应元素差值的平方和再开方，返回两个数组之间的欧几里得距离值。当输入数组长度不一致时，方法会返回0作为默认值。欧几里得距离算法常用于比较两个数组之间的相似度，是数据分析和机器学习中的基础距离度量方法。
【模式识别与机器学习（8）】主要算法与技术（下篇：高级模型与集成方法）之 元学习与集成方法：组合多个学习器来提高整体性能
hiliang521的博客
12-02 802
【模式识别与机器学习（8）】主要算法与技术（下篇：高级模型与集成方法）之 元学习
Leetcode 68 搜索插入位置 | 寻找比目标字母大的最小字母
im_AMBER的博客
12-04 785
你的错误逻辑正确逻辑找到 target 时返回 mid-1找到 target 时，继续向右查找（因为需要「大于」target 的最小字符）target <letters [mid] 时，mid 是候选，需保留，right=mid（左闭右开）或不立即排除 mid循环结束直接返回 letters [0]循环结束后，先判断 left 是否越界：越界则返回 letters [0]，否则返回 letters [left]初始right的取值与「越界判断」不匹配；
dfs|mask^翻转
一个人知道自己为什么而活，他就能够接收任何一种生活
11-30 165
注意到：灯泡状态周期是6。
2025年全国大学生统计科学与算法编程挑战赛——算法赛道（一）
qq_73044452的博客
12-01 290
摘要：本文包含三个编程问题的解决方案。1) 贪吃蛇问题：通过解析移动指令计算蛇最终所在格子的编号；2) 经济小鱼问题：计算前两局存钱、后两局花钱，最终剩余指定金币的方案数；3) 小理吃甜食问题：模拟多轮糖果挑选过程，计算小理获得的最大总糖果值。每个问题都给出了完整的C++实现代码，涉及字符串处理、数学计算和模拟算法等技术。
【剑斩OFFER】算法的暴力美学——数青蛙
最新发布
就业知识博客
12-04 268
力扣1419题：数青蛙
[优选算法专题十.哈希表 ——NO.55~57 两数之和、判定是否互为字符重排、存在重复元素]
2401_83386596的博客
12-03 611
两数之和问题的最优解法采用哈希表实现O(n)时间复杂度，通过存储元素值与下标的映射关系，快速查找互补值。字符重排判定问题通过单哈希数组统计字符出现次数，先加后减并实时校验，确保字符种类和数量完全一致。存在重复元素问题使用哈希集合检测重复元素，遍历数组时检查元素是否已存在于集合中。三种解法均利用哈希结构优化查找效率，将时间复杂度从暴力解法的O(n²)降至O(n)，是典型空间换时间策略的工业级实现。
强化学习[page13]【chapter7】时序差分方法算法介绍
4AM_明朝百晓生
12-01 518
其次，式(7.1)中的TD算法仅能估计给定策略的状态值。尽管如此，本节介绍的TD算法非常基础，对理解本章其他算法至关重要。例如，本章介绍的所有算法都属于时序差分学习的范畴。为简洁起见，式(7.2)常被省略，但必须意识到若缺少该式，算法在数学上将不完整。TD 方法的一个特点是，它在每个时间步更新其值估计，而 MC 方法则要等到回合结束才更新。TD学习的核心思想是基于新获得的信息来修正当前对状态值的估计。因此，TD误差不仅反映两个时间步之间的差异，更重要的是反映了估计值。反映了时间步t与t+1之间的差异。
红包分配算法的严格数学理论与完整实现
12-03 645
红包分配问题可以严格定义为： 定义 1.1（红包分配问题）: 给定总金额 M>0M > 0M>0 和参与人数 n∈N+n \in \mathbb{N}^+n∈N+，分配函数 f:{1,2,...,n}→R+f: \{1, 2, ..., n\} \rightarrow \mathbb{R}^+f:{1,2,...,n}→R+ 需要满足：设 Ω\OmegaΩ 为样本空间，F\mathcal{F}F 为事件域，PPP 为概率测度： 1.2.2 随机变量性质 定义随机变量 XiX_iXi​ 表示第 iii 个人获
基于A*算法和概率路图的三维路径规划方法研究与Matlab实现
Dev7z的博客
12-01 352
随着机器人技术的迅猛发展，路径规划作为机器人自主导航中的核心问题之一，已经引起了广泛的研究关注。传统的二维路径规划方法在许多实际应用中已不再适用，尤其是在复杂的三维环境中，路径规划面临着更多的挑战，如地形复杂性、障碍物多样性以及路径的优化等问题。因此，三维路径规划方法成为了当前研究的热点。
力扣每日一题：统计梯形的数目
yyssas的博客
12-03 136
同时，由于这里只是统计有平行边的四边形，会出现平行四边形，因为两对边都是平行边，因此被统计了两次。对于平行四边形，要判断，就是通过两个对角线的中点是相同的。因此，只要对角线的中点是相同的，然后找所有不同k的边，就可以顺利统计出平行四边形的个数。此处，首先要先统计所谓平行的边，判断依据就是斜率相同且截距不同，因此，要统计平行的边组成的梯形的个数，就是找k相同，b不同的。因此，要用一个哈希表，外层存k，内存存b，这样才能实现遍历的时候正确统计平行边个数。个点在笛卡尔平面上的坐标。给你一个二维整数数组。
蛇群算法在多目标优化问题中的应用及MATLAB实现
资源摘要信息: "智能优化算法-蛇群算法" 蛇群算法（Snake Optimizer）是一种...以上资源为从事智能优化算法研究与应用的学者和工程师提供了实用的工具和参考，有助于理解和实现基于蛇群算法的多目标优化问题解决方案。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值