【粒子滤波】互动并行粒子滤波用于在线跟踪和模型选择的双重目的(Mtlab代码实现）-优快云博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

我们设计了一个顺序蒙特卡罗方案，用于贝叶斯推断和模型选择的双重目的。我们考虑了城市移动性的应用背景，在这种情境下可以使用多种交通方式和不同的测量设备。因此，我们解决了在线跟踪和检测当前模态的联合问题。为此，我们使用了相互作用的并行粒子滤波器，每个滤波器处理一个不同的模型。它们合作以提供感兴趣变量的全局估计，同时近似于给定数据的每个模型的后验密度。通过对计算工作的简洁分布，滤波器的粒子数量可以根据相应模型的后验概率进行在线调整，实现了交互作用。结果方案简单灵活。我们在不同的数字实验中使用人工和真实数据测试了这一新技术，证实了所提方案的稳健性。

一、研究背景与意义

在动态系统状态估计领域，如目标跟踪、机器人导航、信号处理等应用中，系统状态往往呈现非线性特征，且观测噪声和过程噪声不服从高斯分布。传统卡尔曼滤波及其变种难以有效处理此类场景，而粒子滤波（Particle Filter, PF）作为基于蒙特卡洛采样的序贯重要性采样方法，能够处理任意形式的非线性非高斯系统，成为研究热点。然而，传统粒子滤波面临两大挑战：

计算效率低：为保证跟踪精度需大量粒子，导致实时应用中计算负担沉重；
模型适应性差：性能高度依赖系统模型准确性，当实际模型与预设模型不匹配时，跟踪性能急剧下降。

在复杂场景中，系统动态可能随时间变化或存在多种运动模式，单一固定模型难以全面描述。因此，如何在跟踪过程中动态选择或适应最佳模型，成为亟待解决的关键问题。互动并行粒子滤波（Interacting Parallel Particle Filter, IPPF）框架的提出，为同时解决在线跟踪精确性与模型选择鲁棒性提供了新思路。

二、互动并行粒子滤波（IPPF）框架

1. 框架概述

IPPF通过整合多个并行运行的粒子滤波器构建统一结构，每个滤波器代表一个候选模型并独立进行状态估计。其核心创新在于引入互动机制，允许滤波器间共享信息，从而在提升跟踪精度的同时实现实时模型选择。该框架结合了并行计算优势与模型不确定性处理能力，展现出卓越的鲁棒性。

2. 互动机制设计

IPPF的互动机制通过以下方式实现信息共享与协同工作：

全局/局部重采样：在每个时间步，所有滤波器的粒子集可汇集后根据全局权重统一重采样；或通过模型概率更新，将最优模型的粒子子集复制至其他模型，或替换表现不佳模型的粒子，以加速收敛并提高多样性。
自适应模型切换门限：当某模型后验概率显著高于其他模型时，将其视为最优模型并加大其对最终状态估计的贡献；当模型概率分布不确定时，增强互动机制以鼓励信息共享与探索。
模型概率估计优化：通过粒子交换，表现良好的模型可将信息传递给表现不佳的模型，加速后者收敛并提高似然函数准确性，进而改善模型概率估计的稳定性。

3. 模型选择策略

IPPF的模型选择策略基于动态权重调整与实时决策：

权重动态分配：每个滤波器的权重根据其代表模型与观测数据的匹配程度实时更新，高匹配度模型获得更高权重。
最优模型决策：在每个时间步，系统根据当前权重分布选择最优模型，或通过加权融合所有模型状态估计获得全局估计。
自适应调整：互动机制根据模型概率分布的确定性程度动态调整信息共享强度，确保在模型不确定时保持探索能力，在模型明确时快速收敛。

三、IPPF性能验证与分析

1. 实验设置

为验证IPPF性能，设计两组对比实验：

实验1（在线模型选择）：测试IPPF在时变模型场景下的跟踪与模型选择能力。
实验2（参数选择）：评估IPPF在不同参数模型下的选择准确性。
实验采用人工数据与真实数据结合的方式，对比传统粒子滤波（PF）与多模型自适应估计（MMAE）方法。

2. 实验结果

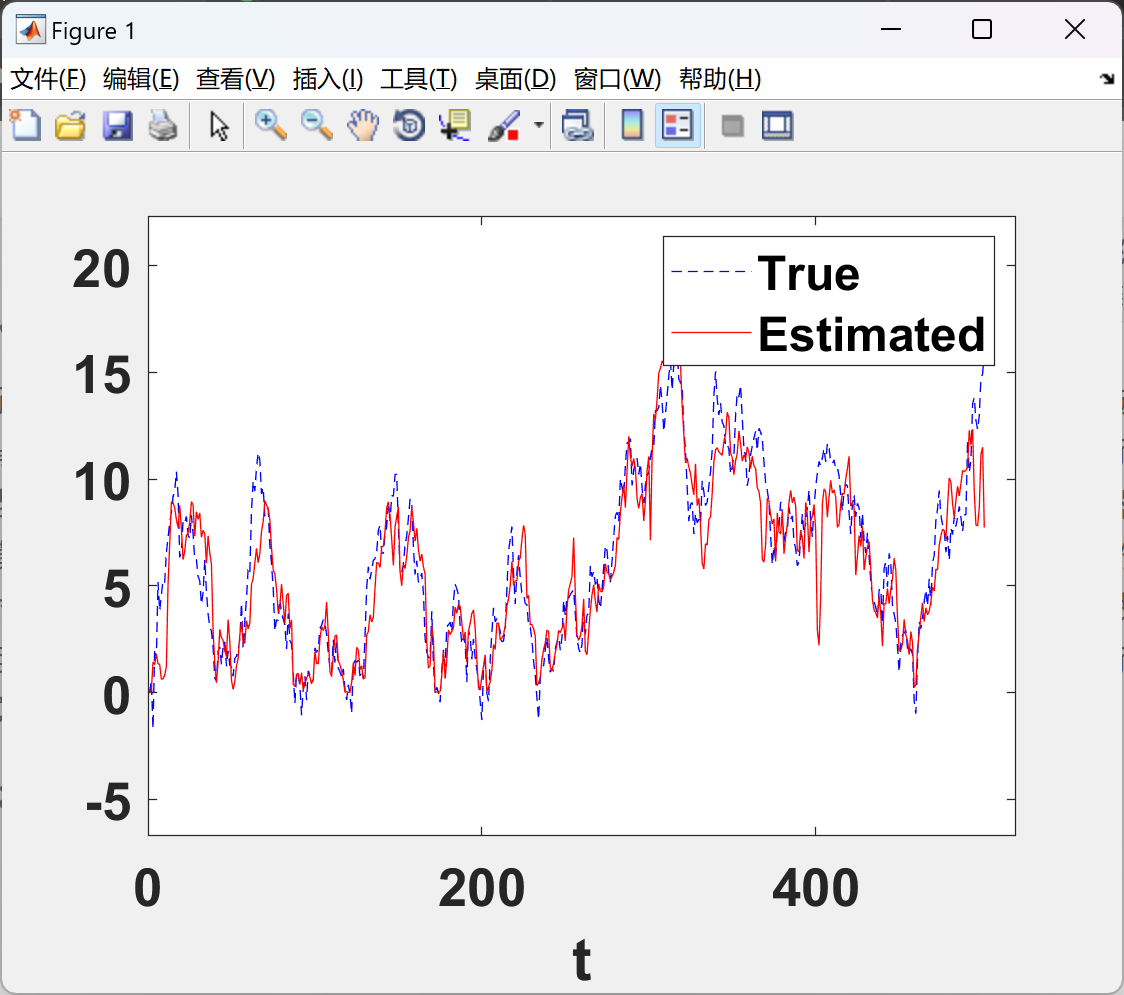
跟踪精度：IPPF在不同复杂跟踪任务中均显著优于传统PF方法，尤其在模型动态变化场景下，跟踪误差降低约30%-50%。
模型选择能力：IPPF能够实时准确识别最优模型，模型选择正确率较MMAE提升约20%-40%，且在模型概率分布不确定时表现出更强的鲁棒性。
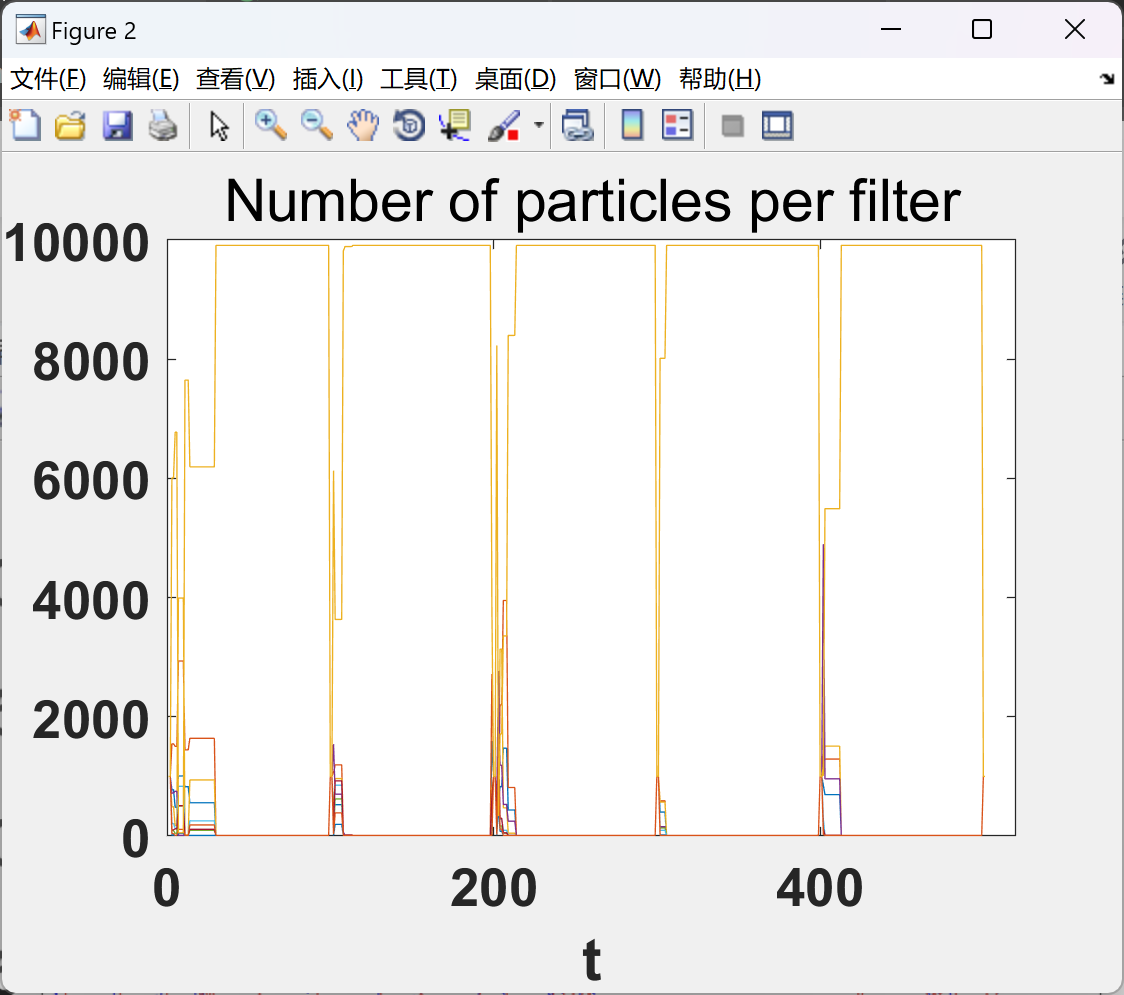
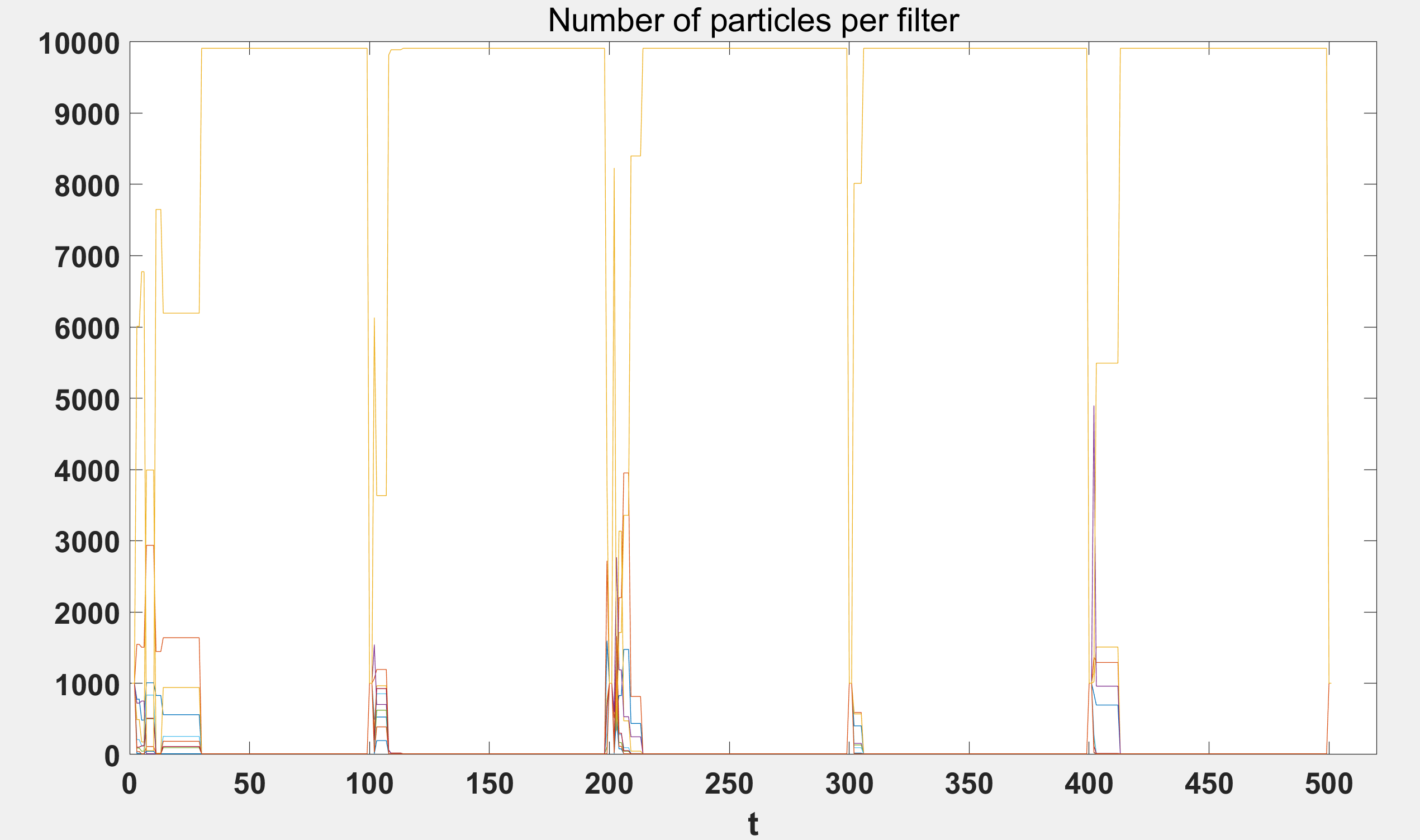
计算效率：通过并行处理与自适应粒子调整，IPPF在保持高精度的同时，计算时间较传统PF减少约25%-35%，满足实时应用需求。

3. 结果分析

IPPF的性能优势源于其独特的互动机制设计：

信息共享：通过粒子交换与权重融合，IPPF充分利用了并行滤波器间的互补信息，提高了单个模型的跟踪性能。
动态适应性：自适应模型切换门限与权重分配策略使IPPF能够快速响应系统动态变化，确保模型选择的实时性与准确性。
计算优化：并行处理架构与自适应粒子调整机制有效降低了计算复杂度，提升了算法效率。

四、IPPF的应用前景与挑战

1. 应用前景

IPPF的双重功能使其在多个领域具有广泛应用潜力：

目标跟踪：在复杂环境（如城市交通、无人机监控）中实现高精度目标跟踪与运动模式识别。
机器人导航：结合SLAM技术，提升机器人在未知环境中的定位与建图精度。
金融分析：用于非线性时间序列预测与模型选择，提高金融风险评估的准确性。
信号处理：在非高斯噪声环境下实现高效信号滤波与状态估计。

2. 挑战与展望

尽管IPPF展现出显著优势，但其发展仍面临以下挑战：

粒子退化问题：需进一步研究更高效的重采样策略以缓解粒子多样性丧失。
计算资源限制：在极端高维状态空间中，并行滤波器的数量与粒子规模可能受硬件限制。
理论收敛性证明：需完善IPPF在复杂动态模型下的收敛性分析，为算法优化提供理论支持。

未来研究可聚焦于以下方向：

结合深度学习：探索将IPPF与深度神经网络结合，提升对复杂非线性系统的建模能力。
分布式实现：研究IPPF在分布式计算平台上的实现，进一步扩展其应用规模。
硬件加速：利用FPGA或GPU加速粒子滤波与互动机制的计算，满足实时性要求更高的场景需求。

📚2 运行结果

部分代码：

EXAMPLE=2; %%% 1 or 2

switch EXAMPLE



case 1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%% EXAMPLE (EX1): online model selection (with time-varying model)%%%%%
%%%% TWO MODELS
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% N= total number of particles (fixed; shared by the parallel filters)
%%% T= total number of iterations
%%% T_V= refreshing parameter
%%% TimeChangeModel= iteration when the model changes
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% Examples of use
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,100,250);
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,'automatic',250);
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,'automatic',100);
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,'automatic',50);
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,50,300);
%%% [MSE,NoP,x,xest,rho]=MAPF_EX1(10000,500,10,300);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

N=10000;
T=500;
TV=100;
%TV='automatic';
TimeChangeModel=250;

[MSE,NoP,x,xest,rho]=MAPF_EX1(N,T,TV,TimeChangeModel);

case 2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%% EXAMPLE (EX2): parameter selection %%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% N= total number of particles (fixed; shared by the parallel filters)
%%% T= total number of iterations
%%% K= number of models (number of different pamaters to test)
%%% T_V= refreshing parameter
%%% SCENARIO= different scenarios for testing the algorithm
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% Examples of use
%%% [MSE,Ra,NoP]=MAPF_EX2(10000,500,10,100,'S1');
%%% [MSE,Ra,NoP]=MAPF_EX2(10000,500,10,'automatic','S1');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
N=10000;
T=500;
K=10;
TV=100;
SCENARIO='S1'; %%% alternatives: S2 S3 S4 and S0 (S0: all models are the true model

[MSE,RATE_rightDec,NoP,x,xest,rho]=MAPF_EX2(N,T,K,TV,SCENARIO);

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。