【经济调度】基于蜜蜂算法的经济调度（Matlab实现）

原创已于 2025-04-17 19:28:42 修改 · 964 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-04-16 19:47:19 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言

经济调度是电力系统运行中的核心问题之一，其目标是在满足电力系统各种约束条件的前提下，合理分配各发电单元的发电功率，使发电总成本最小化，同时确保系统的安全稳定运行。随着电力系统规模的不断扩大和复杂性的增加，传统的经济调度方法在处理大规模、非线性、多约束的优化问题时面临着诸多挑战。蜜蜂算法作为一种新兴的智能优化算法，具有较强的全局搜索能力和自适应能力，为解决电力系统经济调度问题提供了新的思路和方法。

二、经济调度问题描述

目标函数

经济调度的主要目标是最小化发电总成本，通常可以表示为各发电单元发电成本之和。发电成本一般是发电功率的二次函数，可表示为：
F=∑i=1n(aiPi2+biPi+ci)
其中，n 为发电单元的数量，Pi 为第 i 个发电单元的发电功率，ai、bi、ci 为第 i 个发电单元的成本系数。

约束条件

功率平衡约束：发电功率总和应等于系统的总负荷需求加上网络损耗，即
∑i=1nPi=PD+PL
其中，PD 为系统的总负荷需求，PL 为网络损耗。
发电功率上下限约束：每个发电单元的发电功率应在其允许的上下限范围内，即
Pi,min≤Pi≤Pi,max
其中，Pi,min 和 Pi,max 分别为第 i 个发电单元的最小和最大发电功率。
其他约束：还可能包括机组爬坡速率约束、输电线路容量约束等。

三、蜜蜂算法原理

蜜蜂的行为模式蜜蜂算法模拟了蜜蜂在寻找花蜜过程中的行为，主要包括以下三种行为：雇佣蜂行为：雇佣蜂负责在其当前所在的蜜源附近进行局部搜索，以寻找更优的蜜源。它们根据蜜源的质量（适应度值）来决定是否更新当前蜜源。跟随蜂行为：跟随蜂在蜂巢中等待，根据雇佣蜂带回的信息选择一个蜜源进行搜索。它们会选择适应度值较高的蜜源进行搜索，以提高找到更优蜜源的概率。侦察蜂行为：侦察蜂负责在整个搜索空间中随机搜索新的蜜源，以扩大搜索范围，避免算法陷入局部最优。

算法流程 1. 初始化：随机初始化一群蜜源（解），每个蜜源代表一种发电单元的功率分配方案。同时，为每个蜜源分配一个雇佣蜂。 2. 雇佣蜂搜索：每个雇佣蜂在其当前所在的蜜源附近进行局部搜索，生成一个新的蜜源。如果新蜜源的适应度值优于当前蜜源，则更新当前蜜源。 3. 跟随蜂选择：根据各蜜源的适应度值，跟随蜂选择一个蜜源进行搜索。适应度值越高的蜜源被选中的概率越大。 4. 侦察蜂搜索：如果某个蜜源在一定次数的迭代中没有得到改进，则将其放弃，由侦察蜂在整个搜索空间中随机生成一个新的蜜源。 5. 终止条件判断：判断是否满足终止条件（如达到最大迭代次数或适应度值收敛到一定程度）。如果满足，则输出最优解；否则，返回步骤 2 继续迭代。

四、基于蜜蜂算法的经济调度实现

编码方式

将发电单元的发电功率作为决策变量，每个蜜源可以表示为一个向量 [P1,P2,⋯,Pn]，其中 Pi 为第 i 个发电单元的发电功率。

适应度函数设计

适应度函数用于评估每个蜜源的优劣，通常可以将目标函数的倒数作为适应度函数，即
f=F1
其中，F 为发电总成本。

约束处理

在算法的搜索过程中，需要对各种约束条件进行处理。常见的约束处理方法包括惩罚函数法、修复法等。惩罚函数法是在适应度函数中加入惩罚项，对违反约束条件的解进行惩罚；修复法是在生成新解后，对违反约束条件的解进行修复，使其满足约束条件。

五、优势与应用前景

优势全局搜索能力强：蜜蜂算法通过侦察蜂的随机搜索和雇佣蜂、跟随蜂的局部搜索相结合，能够在整个搜索空间中寻找最优解，避免陷入局部最优。自适应能力好：算法能够根据蜜源的适应度值自动调整搜索策略，在搜索初期更注重全局搜索，在搜索后期更注重局部搜索，提高了搜索效率。易于实现：蜜蜂算法的原理简单，实现过程相对容易，不需要复杂的数学模型和计算方法。应用前景电力系统经济调度：可以应用于传统电力系统的经济调度，也可以应用于含分布式电源、储能装置等的新型电力系统的经济调度。其他优化问题：除了电力系统经济调度，蜜蜂算法还可以应用于其他领域的优化问题，如工程设计、物流配送、资源分配等。

六、挑战与发展方向

挑战：参数设置困难：蜜蜂算法的性能受到多个参数的影响，如种群规模、雇佣蜂数量、跟随蜂数量、侦察蜂搜索概率等，参数的设置需要根据具体问题进行调整，难度较大。收敛速度较慢：在处理大规模、复杂的优化问题时，蜜蜂算法的收敛速度可能较慢，需要较长的计算时间。

发展方向：参数自适应调整：研究参数自适应调整策略，使算法能够根据搜索过程中的信息自动调整参数，提高算法的性能。与其他算法融合：将蜜蜂算法与其他优化算法（如遗传算法、粒子群算法等）进行融合，发挥各自的优势，提高算法的收敛速度和搜索精度。并行计算：利用并行计算技术加速蜜蜂算法的搜索过程，提高算法的计算效率。基于蜜蜂算法的经济调度方法为解决电力系统经济调度问题提供了一种有效的途径。虽然目前还存在一些挑战，但随着研究的不断深入和技术的不断发展，相信该方法将在电力系统及其他领域得到更广泛的应用。

📚2 运行结果

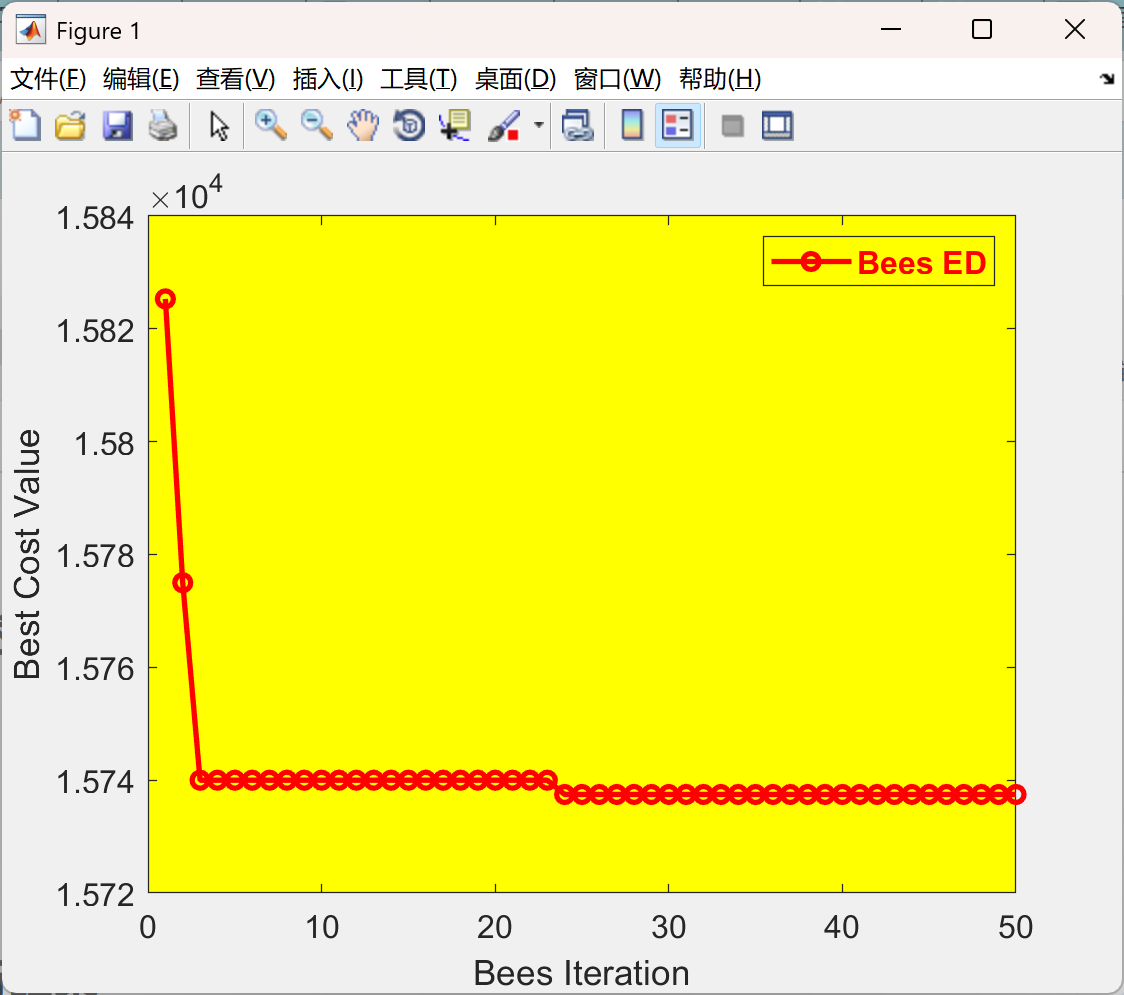
部分代码：

%% Bees Algorithm (BA) Economic Dispatching (ED)
% P = power plants
% CTotal = the cost
% q= violation
% PL = power loss
% PTotal = all powers
% PD = power demand
clc;
clear;
close all;

%% Problem 
model=MakeModel();
CostFunction=@(x) Cost(x,model);        % Cost Function
nVar=model.nPlant;                      % Number of Decision Variables
VarSize=[1 nVar];                       % Size of Decision Variables Matrix
VarMin=0;                               % Lower Bound of Variables
VarMax=1;                               % Upper Bound of Variables

%% Bees Algorithm Parameters
MaxIt = 50;                               % Maximum Number of Iterations
nScoutBee = 5;                            % Number of Scout Bees
nSelectedSite = round(0.5*nScoutBee);     % Number of Selected Sites
nEliteSite = round(0.4*nSelectedSite);    % Number of Selected Elite Sites
nSelectedSiteBee = round(0.5*nScoutBee);  % Number of Recruited Bees for Selected Sites
nEliteSiteBee = 2*nSelectedSiteBee;       % Number of Recruited Bees for Elite Sites
r = 0.1*(VarMax-VarMin);	              % Neighborhood Radius
rdamp = 0.95;                             % Neighborhood Radius Damp Rate

%% Start
% Empty Bee Structure
empty_bee.Position = [];
empty_bee.Cost = [];
empty_bee.Sol = [];
% Initialize Bees Array
bee = repmat(empty_bee, nScoutBee, 1);
% Create New Solutions
for i = 1:nScoutBee
bee(i).Position = unifrnd(VarMin, VarMax, VarSize);
[bee(i).Cost bee(i).Sol] = CostFunction(bee(i).Position);
end
% Sort
[~, SortOrder] = sort([bee.Cost]);
bee = bee(SortOrder);
% Update Best Solution Ever Found
BestSol = bee(1);
% Array to Hold Best Cost Values
BestCost = zeros(MaxIt, 1);

%% Bees Algorithm Body
for it = 1:MaxIt
% Elite Sites
for i = 1:nEliteSite
bestnewbee.Cost = inf;
for j = 1:nEliteSiteBee
newbee.Position = BeeDance(bee(i).Position, r);
[newbee.Cost newbee.Sol] = CostFunction(newbee.Position);
if newbee.Cost<bestnewbee.Cost
bestnewbee = newbee;
end
end
if bestnewbee.Cost<bee(i).Cost
bee(i) = bestnewbee;
end
end
% Selected Non-Elite Sites
for i = nEliteSite+1:nSelectedSite
bestnewbee.Cost = inf;
for j = 1:nSelectedSiteBee
newbee.Position = BeeDance(bee(i).Position, r);
[newbee.Cost newbee.Sol] = CostFunction(newbee.Position);
if newbee.Cost<bestnewbee.Cost
bestnewbee = newbee;
end
end
if bestnewbee.Cost<bee(i).Cost
bee(i) = bestnewbee;
end
end
% Non-Selected Sites
for i = nSelectedSite+1:nScoutBee
bee(i).Position = unifrnd(VarMin, VarMax, VarSize);
[bee(i).Cost bee(i).Sol] = CostFunction(bee(i).Position);
end
% Sort
[~, SortOrder] = sort([bee.Cost]);
bee = bee(SortOrder);
% Update Best Solution Ever Found
BestSol = bee(1);
% Store Best Cost Ever Found
BestCost(it) = BestSol.Cost;
% Display Iteration Information
disp(['In Iteration No ' num2str(it) ': Bees Cost is = ' num2str(BestCost(it))]);
% Damp Neighborhood Radius
r = r*rdamp;
end

% Plot ITR
plot(BestCost,'-or', 'LineWidth', 2);
xlabel('Bees Iteration');
ylabel('Best Cost Value');
ax = gca; 
ax.FontSize = 12; 
set(gca,'Color','y')
legend({'Bees ED'},'FontSize',12,'FontWeight','bold','TextColor','r');
%% Results
BestSol
%
BestSol.Sol
%
Res=BestSol.Sol.PTotal-BestSol.Sol.PL-model.PD