AtCoder AGC006D（LgAT2165） Median Pyramid Hard 题解（AtCoder风格，二分答案）

最新推荐文章于 2024-04-12 16:51:29 发布

原创最新推荐文章于 2024-04-12 16:51:29 发布 · 483 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解

AtCoder 专栏收录该内容

4 篇文章

订阅专栏

该博客介绍了AtCoder AGC006D题目，这是一个关于金字塔中位数问题的算法题。博主分享了题目的背景、输入输出格式及样例，并详细解释了使用二分法寻找塔顶数字的思路。内容包括如何根据数字大小关系设置二分答案，并通过判断连续的1或0来确定最终答案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原链接：
AtCoder：点我QωQ
洛谷：点我QωQ

题意简述

有一个金字塔，长这样：

底层有 $2 n - 1$ 个元素。给定 $n$ 和这 $2 n - 1$ 个元素，依次向上填，某一个格子上填的数是它下面三个数中的中位数（显然每个格子下面都有三个数）。求塔顶的那个数。

数据

输入

第一行是一个 $n$ 。接下来一行给定 $2 n - 1$ 个数。

输出

塔顶的那个数

样例

输入
4
1 6 3 7 4 5 2
输出
4

输入
2
1 2 3
输出
2

思路

这题是十分经典的 $A t C o d e r$ 岛国题风格。像这种东西，几乎很难能想到是用二分答案做。以后记住，看到这种岛国题，就是二分答案，不用想别的。。。（别的真的没思路，我想了一天不会，还是AllureLove巨佬提醒我是二分答案，我才差不多明白。。。）

好的我们来看看如何二分。假设我们现在考虑 $M i d$ 是否珂能是最后的答案。我们会发现，中位数什么的具体只和大小关系有关，和具体是多少没有太大的关系。所以，我们设比 $M i d$ 大的是 $1$ ，其余（即 $< = M i d$ 的）设为 $0$ 。
（从洛谷题解上盗张图）

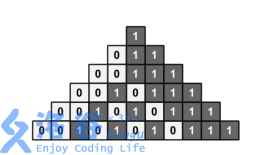
然后我们会发现，如果有一个连续的 $1$ 或 $0$ ，那么就会一路上去，并且往中间靠。那么，我们只要找离中间最近的是 $0$ 还是 $1$ ，就珂以确定塔顶是 $0$ 还是 $1$ 了。
如果塔顶是 $0$ ，说明答案 $< = M i d$ ，否则答案就 $> M i d$ 。这样我们就珂以确定答案是小还是大，显然珂以二分。
（那么如果没有连续的怎么办？特判即可，找一下规律，发现此时塔顶和第一个的 $01$ 值是相同的）

代码：

#include<bits/stdc++.h>
using namespace std;
namespace Flandle_Scarlet
{
    #define N 200100
    int n,a[N];

    void Input()
    {
        scanf("%d",&n);
        for(int i=1;i<(n<<1);++i)
        {
            scanf("%d",&a[i]);
        }
    }

    int greater2(int x,int a,int b)//a,b都>x，用来判连续的1
    {
        return (a>x) and (b>x);
    }
    int less2(int x,int a,int b)//a,b都<=x，用来判连续的0
    {
        return (a<=x) and (b<=x);
    }
    bool check(int Mid)//判断答案是否<=Mid
    {
        for(int i=0;i<n-1;++i)//枚举和中间的距离
        {
            if (greater2(Mid,a[n+i],a[n+i+1]) or greater2(Mid,a[n-i],a[n-i-1])) return 0;//连续的1
            if (less2(Mid,a[n+i],a[n+i+1]) or less2(Mid,a[n-i],a[n-i-1])) return 1;//连续的0
            //左右都要考虑
        }
        return (a[1]<=Mid);//如果没有连续的，特判
    }
    void Solve()
    {
        int Low=1,High=(n<<1)-1;
        while(Low<High)
        {
            int Mid=(Low+High)>>1;
            if (check(Mid))
            {
                High=Mid;
            }
            else
            {
                Low=Mid+1;
            }
        }
        printf("%d\n",High);//二分
    }
    void Main()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        Input();
        Solve();
    }
    #undef N//200100
};
main()
{
    Flandle_Scarlet::Main();
    return 0;
}

回到总题解界面