1.已知 a∈Ra\in Ra∈R .设函数 f(x)={x2−2ax+2a,x≤1x−alnx,x>1f(x)=\begin{cases}x^2-2ax+2a , x\leq1 \\ x-a\ln x , x>1\end{cases}\quadf(x)={x2−2ax+2a,x≤1x−alnx,x>1 ，若关于 xxx 的不等式 f(x)≥0f(x)\geq0f(x)≥0 在 R\rm RR 上恒成立，则 aaa 的取值范围为 ()(\qquad)()
A.[0,1]B.[0,2]A.[0,1]\qquad\qquad\qquad B.[0,2]A.[0,1]B.[0,2]
C.[0,e]D.[1,e]C.[0,\rm e]\qquad\qquad\qquad D.[1,\rm e]C.[0,e]D.[1,e]
解析
设 f1(x)=x2−2ax+2a,f2(x)=x−alnxf_1(x)=x^2-2ax+2a,f_2(x)=x-a\ln xf1(x)=x2−2ax+2a,f2(x)=x−alnx ，对于 f1(x)f_1(x)f1(x) 有对称轴 x=ax=ax=a ，且 f1(1)=1,f1(0)=2af_1(1)=1,f_1(0)=2af1(1)=1,f1(0)=2a .
当 a<0a<0a<0 时，存在 x0≤1x_0\leq1x0≤1 使得 f1(x0)<0f_1(x_0)<0f1(x0)<0 ，故不符.
当 0≤a≤10\leq a\leq 10≤a≤1 时，f1(x)=x2−2ax+2a=(x−a)2+a(2−a)>0f_1(x)=x^2-2ax+2a=(x-a)^2+a(2-a)>0f1(x)=x2−2ax+2a=(x−a)2+a(2−a)>0 f2(x)=x−alnx≥x−a(x−1)=(1−a)x+a≥0f_2(x)=x-a\ln x\geq x-a(x-1)=(1-a)x+a\geq0f2(x)=x−alnx≥x−a(x−1)=(1−a)x+a≥0符合.
当 a>1a>1a>1 时，f1(x)f_1(x)f1(x) 在 (−∞,1](-\infty,1](−∞,1] 上单调递减，则 f1(x)≥f1(1)=1f_1(x)\geq f_1(1)=1f1(x)≥f1(1)=1 .求得 f2′(x)=x−ax{f_2}^{'}(x)=\dfrac{x-a}{x}f2′(x)=xx−a故 f2(x)f_2(x)f2(x) 在 (1,a)(1,a)(1,a) 上单调递减，在 (a,+∞)(a,+\infty)(a,+∞) 上单调递增.依题意有 f2(x)min=f2(a)=a−alna≥0f_2(x)_{\rm min}=f_2(a)=a-a\ln a\geq0f2(x)min=f2(a)=a−alna≥0 ，解得 1<a≤e1<a\leq \rm e1<a≤e .
综上， aaa 的取值范围是 [0,e][0,\rm e][0,e] .
2. 在四边形 ABCDABCDABCD 中，AD//BC,AB=23,AD=5,∠A=30∘AD//BC,AB=2\sqrt{3},AD=5,\angle A=30^\circAD//BC,AB=23,AD=5,∠A=30∘ ，点 EEE 在 CBCBCB 的延长线上，且 AE=BEAE=BEAE=BE ，则 BD→⋅AE→=\overrightarrow{BD}\cdot\overrightarrow{AE}=BD⋅AE=________.
解析
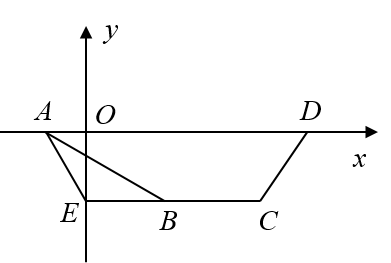
如图，建立平面直角坐标系，则 A(−1,0),E(0,−3),B(2,−3),D(4,0)A(-1,0),E(0,-\sqrt{3}),B(2,-\sqrt{3}),D(4,0)A(−1,0),E(0,−3),B(2,−3),D(4,0) .故BD→⋅AE→=(2,3)⋅(1,−3)=−1\overrightarrow{BD}\cdot\overrightarrow{AE}=(2,\sqrt{3})\cdot(1,-\sqrt{3})=-1BD⋅AE=(2,3)⋅(1,−3)=−1
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
