数量积定值

LB_yifeng

于 2020-02-02 21:36:08 发布

阅读量408

点赞数

CC 4.0 BY-SA版权

分类专栏：高中数学知识

本文链接：https://blog.youkuaiyun.com/LB_yifeng/article/details/104149898

通过解决一道椭圆题目，确定了椭圆的标准方程为4x^2 + 3y^2 = 1，并探讨了当直线变化时，椭圆上两点与x轴上定点连线的点乘积保持为定值的情况，找到定点坐标为(8/11, 0)。" 108594222,7919609,Python金融大数据挖掘：正则表达式实战,"['数据挖掘', 'python', '正则表达式']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【题目】
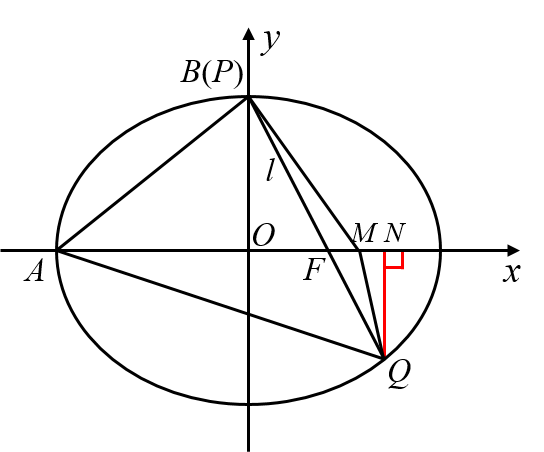
已知椭圆 $C:x2a2+y2b2=1(a>b>0)C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左顶点为 $A$ ，右焦点为 $F$ ，上顶点为 $B$ ，过 $F$ 的直线 $l$ 交椭圆 $C$ 于 $P, Q$ .当 $P$ 与 $B$ 重合时， $△APF\triangle APF$ 与 $△AQP\triangle AQP$ 的面积分别为 $332,9310\dfrac{3\sqrt{3}}{2},\dfrac{9\sqrt{3}}{10}$ .

$(1)$ 求椭圆 $C$ 的方程；
$(2)$ 在 $x$ 轴上找一点 $M$ ，当 $l$ 变化时， $MP→⋅MQ→\overrightarrow{MP}\cdot\overrightarrow{MQ}$ 为定值.

【解析】

$(1)$ 作 $QN⊥xQN\perp x$ 轴于 $N$ ，则 $S△APFS△AQF=POQN=OFNF=53⟹QN=35b,NF=35c⟹P(85c,−35b)\dfrac{S_{\triangle APF}}{S_{\triangle AQF}}=\dfrac{PO}{QN}=\dfrac{OF}{NF}=\dfrac{5}{3}\Longrightarrow QN=\dfrac{3}{5}b,NF=\dfrac{3}{5}c\Longrightarrow P(\dfrac{8}{5}c,-\dfrac{3}{5}b)$