C语言数据结构-满二叉树、完全二叉树的节点数计算

最新推荐文章于 2026-01-06 17:38:45 发布

原创最新推荐文章于 2026-01-06 17:38:45 发布 · 563 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c语言 #算法

数据结构专栏收录该内容

14 篇文章

订阅专栏

一、基本概念

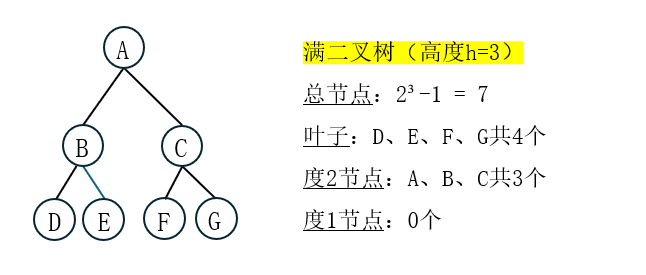
1.1 满二叉树

定义：高度为 h 的二叉树，如果它有最大的节点数（2ʰ-1个），则称为满二叉树。

特征：

每一层都达到最大节点数
所有叶子都在最后一层
每个非叶子节点都有两个子节点
没有度为1的节点（要么0个子，要么2个子）

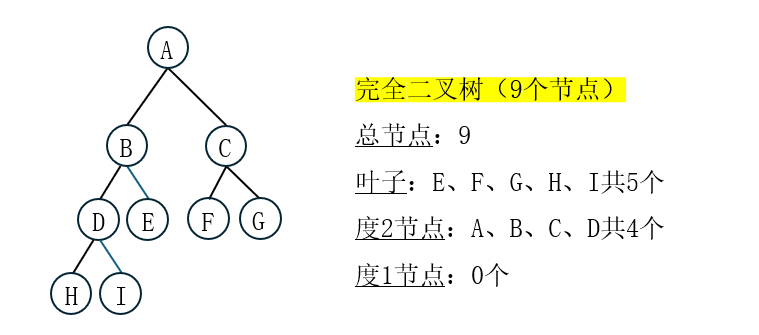
1.2 完全二叉树

定义：高度为 h 的二叉树，除第 h 层外，其他各层都达到最大节点数，且第 h 层的节点都连续集中在最左边。

特征：

叶子节点只在最后两层
最后一层的叶子都靠左排列
度为1的节点最多只有1个
适合用数组存储（没有空洞）

1.3 两种二叉树对比

特性	满二叉树	完全二叉树
度1节点	总是0个	0个或1个
叶子位置	全在最后一层	最后两层
节点公式	N=2ʰ-1	无简单公式
叶子公式	L=2ʰ⁻¹	L=⌈N/2⌉
存储效率	最高（无浪费）	高（数组存储无空洞）
常见应用	理论分析、完美平衡	堆排序、优先级队列

二、代码详解

2.1 满二叉树计算

先检查边界：高度必须>0，否则直接返回
套用公式计算
按顺序输出：先总节点，再叶子，然后度2，最后度1（总是0）

void fullBinaryTree(int height) {
    if (height <= 0) return;  // 第1步：参数检查
    
    // 第2步：核心计算
    int total_nodes = pow(2, height) - 1;      // 公式1：总节点数 = 2^h - 1
    int leaf_nodes = pow(2, height - 1);       // 公式2：叶子数 = 2^(h-1)
    int degree2_nodes = leaf_nodes - 1;        // 公式3：度2节点 = 叶子数 - 1
    
    // 第3步：输出结果
    printf("\n高度为 %d 的满二叉树:\n", height);
    printf("总节点数: %d\n", total_nodes);
    printf("叶子节点数: %d\n", leaf_nodes);
    printf("度2节点: %d\n", degree2_nodes);
    printf("度1节点: 0\n");  // 第4步：满二叉树特性（无度1节点）
}

2.2 完全二叉树计算

边界检查：节点数必须>0
依次计算：高度 → 叶子数 → 度1节点 → 度2节点（用减法）
简洁输出：直接显示所有结果

void completeBinaryTree(int n) {
    if (n <= 0) return;  // 第1步：参数检查
    
    // 第2步：计算三个关键值
    int h = (int)(log2(n)) + 1;          // 公式1：高度 = ⌊log₂n⌋ + 1
    int leaves = (n + 1) / 2;            // 公式2：叶子数 = ⌈n/2⌉
    int degree1 = (n % 2 == 0) ? 1 : 0;  // 公式3：度1节点（偶数1，奇数0）
    int degree2 = n - leaves - degree1;  // 公式4：度2节点 = 总数 - 叶子 - 度1
    
    // 第3步：输出结果
    printf("\n%d个节点的完全二叉树:\n", n);
    printf("高度: %d\n", h);
    printf("叶子数: %d\n", leaves);
    printf("度1节点: %d\n", degree1);
    printf("度2节点: %d\n", degree2);
}

2.3 主函数main

int main() {
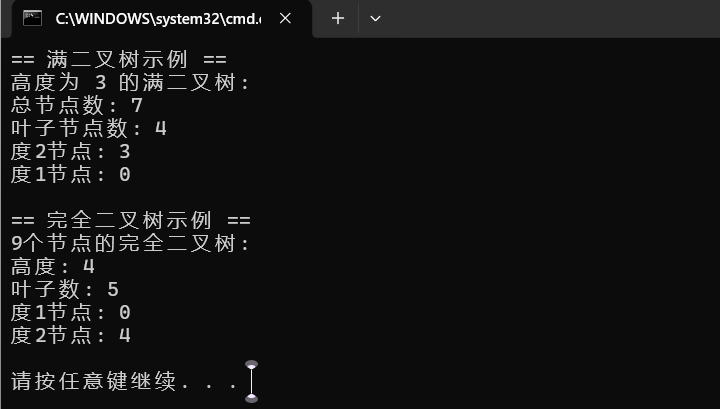
    // 1. 演示满二叉树
    printf("== 满二叉树示例 ==");
    fullBinaryTree(3);  // 高度为3的满二叉树
    
    // 2. 演示完全二叉树
    printf("\n== 完全二叉树示例 ==");
    completeBinaryTree(9);  // 9个节点的完全二叉树
    
    return 0;
}