一、概念
顺序查找:从头到尾逐个比较,简单直接但不要求数据有序,适合小型或无序数据集。
折半查找:每次与中间元素比较,排除一半数据,效率高但要求数据必须有序,适合大型有序数据集。
二、代码详解
2.1 顺序查找函数
这个函数名为sequentialSearch,接受三个参数:一个整型数组arr、数组长度n和要查找的关键字key。函数内部采用一个简单的for循环,从数组的第一个元素开始,逐个与目标关键字进行比较。
如果找到相等的元素,立即返回该元素的下标位置。
如果遍历完整个数组都没有找到匹配的元素,则返回-1作为“未找到”的标识。
#include <stdio.h> // 包含标准输入输出库,提供printf、scanf等函数的声明
// 顺序查找函数
int sequentialSearch(int arr[], int n, int key) { //(整型数组,数组长度,要查找的关键字)
for (int i = 0; i < n; i++) {
if (arr[i] == key) {
return i;
}
}
return -1;
}
2.2 折半查找函数
函数名为binarySearch,参数与顺序查找相同。但这种算法要求输入的数组必须是已经排序好的。函数使用“二分法”思想:初始化两个指针low和high分别指向数组的起始和末尾位置。在循环中,计算中间位置mid,比较中间元素与目标值的大小。
如果相等则直接返回;
如果中间元素小于目标值,说明目标只可能在后半部分,于是调整low指针到mid+1;
反之则调整high指针到mid-1。
如此反复,每次比较都能排除一半的搜索范围,直到找到目标或搜索范围为空。这个算法的效率远高于顺序查找,但前提是数组必须有序。
// 折半查找函数(迭代)
int binarySearch(int arr[], int n, int key) {
int low = 0; // 定义查找范围的左边界,初始为数组起始位置0
int high = n - 1; // 定义查找范围的右边界,初始为数组末尾位置n-1
while (low <= high) { // 当左边界<=右边界时继续查找
int mid = low + (high - low) / 2; // 计算中间位置
if (arr[mid] == key) {
return mid;
} else if (arr[mid] < key) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
2.3 显示数组
用于格式化输出数组内容。它遍历数组并打印每个元素,最后换行,使输出结果更清晰易读。
// 显示数组
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
2.4 主函数main
主函数main是程序的执行入口。首先打印程序标题,然后进行顺序查找测试。这里定义了一个无序数组Arr1,包含了9个整数。通过sizeof运算符计算数组长度——这是C语言中获取数组元素个数的常用技巧:用整个数组的字节大小除以单个元素的字节大小。程序设置要查找的关键字为450,这个值故意不在数组中,以测试“未找到”的情况。调用sequentialSearch函数后,根据返回值判断是否找到,并输出相应信息。
接着进行折半查找测试。这里定义了一个新的有序数组Arr2,包含相同的数值但已按升序排列。程序使用同一个关键字450调用binarySearch函数。由于数组是有序的,折半查找算法可以有效工作。同样地,根据返回值输出查找结果。
int main() {
printf("=== 查找算法测试 ===\n");
// 顺序查找测试
int Arr1[] = {12, 34, 54, 2, 3, 45, 67, 23, 90};
int n1 = sizeof(Arr1) / sizeof(Arr1[0]);
printf("1. 顺序查找测试\n");
printf("数组: ");
printArray(Arr1, n1);
int key = 450;
int result1 = sequentialSearch(Arr1, n1, key);
if (result1 != -1) {
printf("元素 %d 找到,位置: %d\n\n", key, result1);
} else {
printf("元素 %d 未找到\n\n", key);
}
// 折半查找测试
int Arr2[] = {2, 3, 12, 23, 34, 45, 54, 67, 90};
int n2 = sizeof(Arr2) / sizeof(Arr2[0]);
printf("2. 折半查找测试\n");
printf("数组: ");
printArray(Arr2, n2);
// 迭代版本
int result2 = binarySearch(Arr2, n2, key);
if (result2 != -1) {
printf("元素 %d 找到,位置: %d\n", key, result2);
} else {
printf("元素 %d 未找到\n", key);
}
return 0;
}
运行结果1:
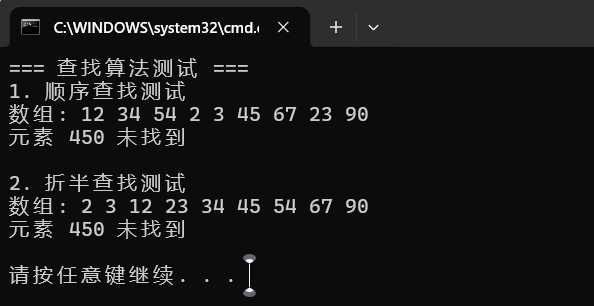
运行结果2:
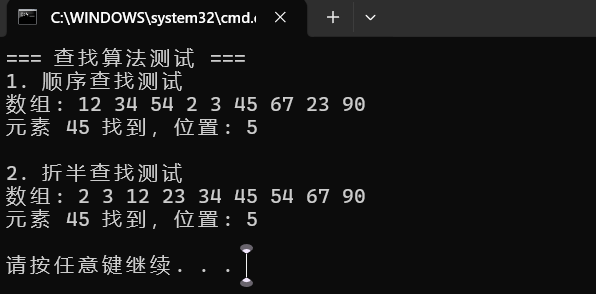
三、总结
这个程序很好地展示了算法实现的基本模式:清晰的函数定义、合理的参数设计、正确的算法逻辑以及完整的测试验证,两种查找算法分别适用于不同的场景:
- 顺序查找不要求数组有序,但效率较低;
- 折半查找效率高,但要求输入数组必须有序;





















 3349
3349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








