C语言数据结构-邻接矩阵图实现（深度/广度）

原创已于 2026-01-08 16:47:58 修改 · 352 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#c语言 #数据结构 #开发语言

于 2026-01-07 00:15:00 首次发布

数据结构专栏收录该内容

14 篇文章

订阅专栏

一、基本概念

1. 什么是图？

图由顶点（节点）和边组成。

2. DFS 和 BFS 是什么？

DFS（深度优先搜索）：像走迷宫，一条路走到底，走不通再回头；
BFS（广度优先搜索）：像水波扩散，从起点一层层向外扩展。

二、代码详解

#include <stdio.h>
#include <stdlib.h>
#define MAX 100  // 最多100个顶点

// 邻接矩阵存储图：graph[i][j]=1表示顶点i到j有边
int graph[MAX][MAX];
int visited[MAX];  // 记录顶点是否被访问过
int n;  // 顶点数

2.1 初始化图

初始化一个空的图，没有任何边。

void initGraph() {
    for(int i = 0; i < n; i++) {
        visited[i] = 0;       // 所有顶点都未访问
        for(int j = 0; j < n; j++) {
            graph[i][j] = 0;  // 所有边都不存在
        }
    }
}

2.2 添加边

void addEdge(int u, int v) {
    graph[u][v] = 1;  // u到v有边
    graph[v][u] = 1;  // v到u也有边（无向图）
}

2.3 DFS（深度优先搜索）递归实现

void DFS(int v) {
    visited[v] = 1;        // 标记当前顶点已访问
    printf("%d ", v);      // 输出顶点
    
    for(int i = 0; i < n; i++) {
        // 如果v到i有边，且i还没被访问
        if(graph[v][i] == 1 && !visited[i]) {
            DFS(i);        // 递归访问i
        }
    }
}

代码逻辑：

2.4 BFS（广度优先搜索）队列实现

void BFS(int start) {
    int queue[MAX], front = 0, rear = 0;
    
    // 重置访问数组
    for(int i = 0; i < n; i++) visited[i] = 0;
    
    visited[start] = 1;      // 标记起点已访问
    printf("%d ", start);    // 输出起点
    queue[rear++] = start;   // 起点入队
    
    while(front < rear) {    // 队列不为空
        int v = queue[front++];  // 出队一个顶点
        
        // 遍历v的所有邻居
        for(int i = 0; i < n; i++) {
            if(graph[v][i] == 1 && !visited[i]) {
                visited[i] = 1;      // 标记访问
                printf("%d ", i);    // 输出
                queue[rear++] = i;   // 入队
            }
        }
    }
}

代码逻辑：

2.5 主函数main

int main() {
    n = 5;  // 5个顶点：0,1,2,3,4
    initGraph();
    
    // 添加边，构建示例图
    addEdge(0, 1);  // 边0-1
    addEdge(0, 2);  // 边0-2
    addEdge(1, 3);  // 边1-3
    addEdge(1, 4);  // 边1-4  
    addEdge(2, 4);  // 边2-4
    
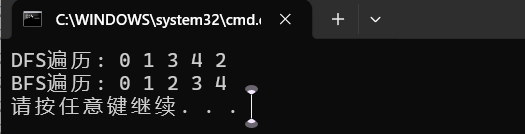
    printf("DFS遍历（深度优先）: ");
    DFS(0);  // 从顶点0开始DFS
    
    printf("\nBFS遍历（广度优先）: ");
    BFS(0);  // 从顶点0开始BFS
    
    return 0;
}