高等数学强化2：一元函数微分学 中值定理 极值点 拐点

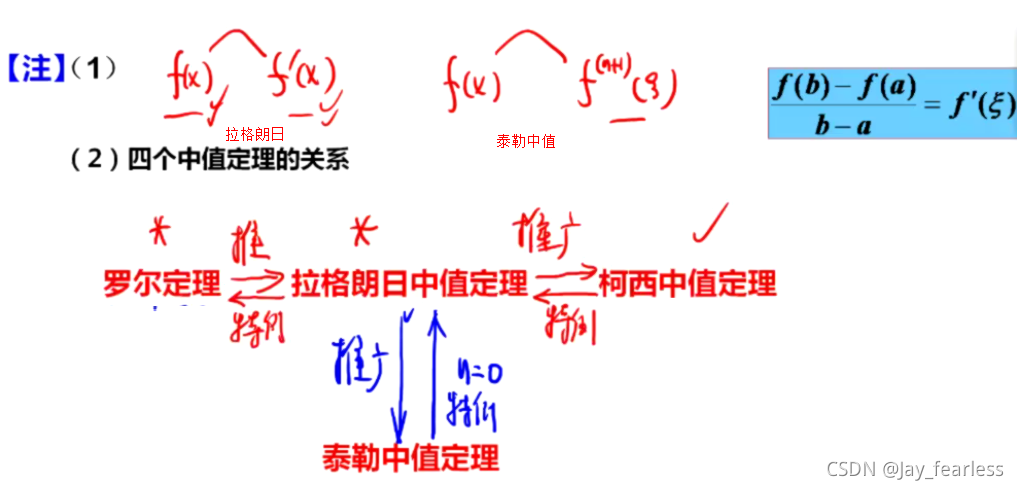
1.四大中值定理：

4个定理之间的联系：

2.极值与最值

函数可导，极值点一定是驻点。
若不可导，极值点、驻点没有必然联系。
找极值，要在导数为0的点或导数不存的的点进行查找。

3.拐点

零点,驻点,极值点指的都是函数y=f(x)的一个横坐标$x_0$,而拐点指的是函数y=f(x)图像上的一个点$(x_0,f(x_0))$。

3.中值定理

齐次情况:

形如$f^{{}^{\prime \prime }}(x)+a{f}^{{}^{\prime }}(x)+bf(x)=0$的问题辅助函数构造：
需要消掉常数$C_1$或$C_2$。

对$h^{{}^{\prime }}(x)+p(x)h(x)=0$之类的函数可以构造辅助函数：
$$G(x)=h(x)e^{\int p(x)dx}$$

非齐次情况

对$h^{{}^{\prime }}(x)+p(x)h(x)=q(x)$之类的函数可以构造辅助函数：
$$G(x)=h(x)e^{\int p(x)dx}-\int q(x)e^{\int p(x)dx}dx$$

有ξ、$\eta$两个未知变量

做法：通过几何找斜率之间的关系，然后运用拉格朗日中值定理解题：

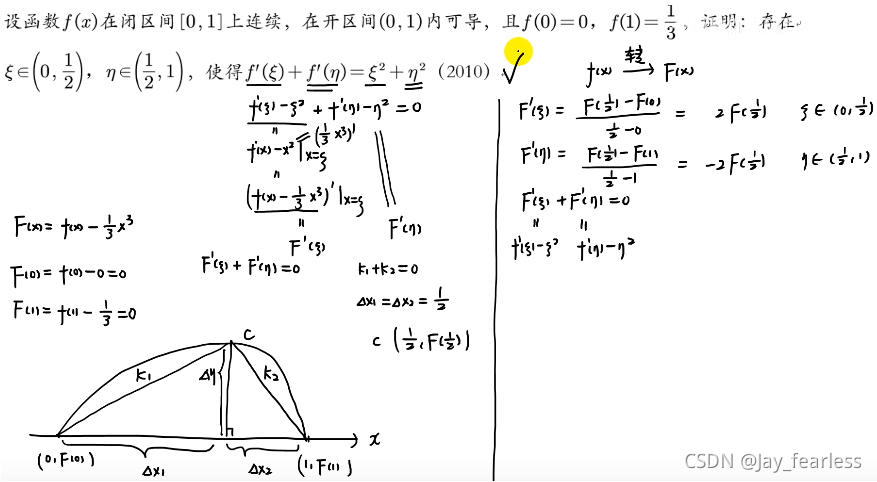
同样利用几何找斜率的关系，用拉格朗日

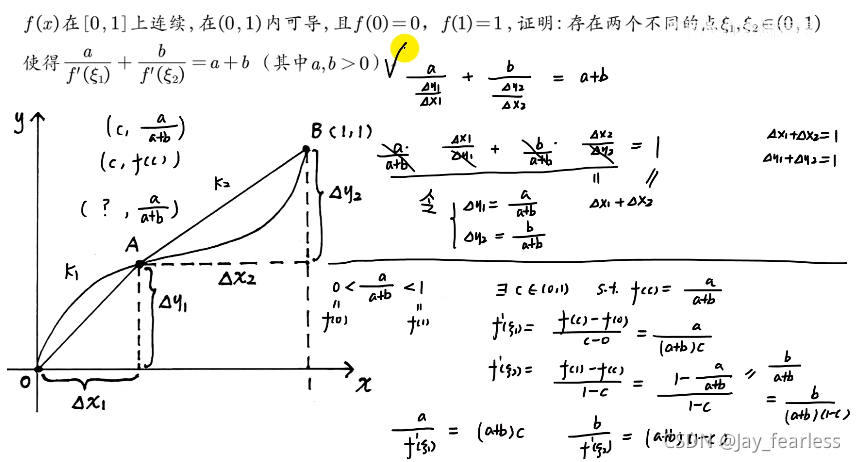
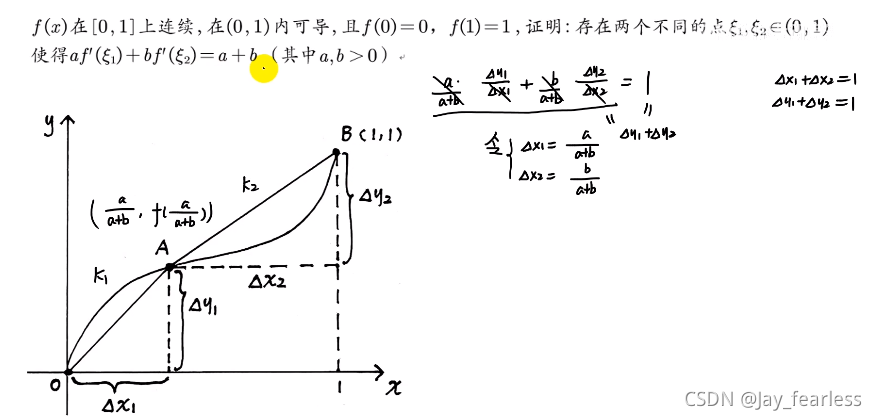
将a+b变为具体值的变型：

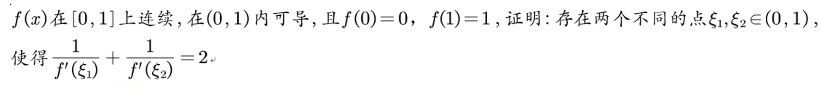
推广到n项：

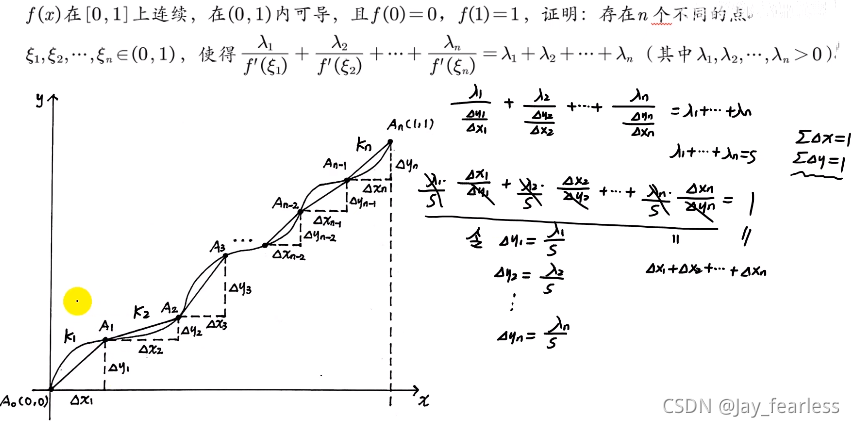
做法同上