栓奶牛：二分更胜DP一筹

栓奶牛

 

解法一：二分

很明显题目说了：最小值最大，满足单调性，因此可以二分

解释一下：题目要求：距离最近的奶牛之间的距离尽可能大。那么也就是说，两头奶牛要尽量间隔的远一些，即间隔大一点，组数少一点。此时有一个小贪心，那就是第一个桩子肯定要选。我们二分题目所求的最大距离（间隔），如果这个间隔k，可行的话，我们要继续看再大一点可不可以，这就是l=mid+1；如果k不行，意味着，间隔太大了，那么我们要调小，就是r=mid-1；这就是所谓的单调性。

二分的复杂度是非常优秀的logn，完全不用担心时间。

 

Code：

#include <bits/stdc++.h>
using namespace std;

int n,k,w[105];

bool check(int x)
{
	int num=1,last=1;
	for(int i=2;i<=k;i++)
	{
		if(w[i]-w[last]>=x)
		{
			num++;
			last=i;
		 } 
	}
	if(num>=n) return 1;
	return 0;
 } 
int main()
{
	cin>>n>>k>>w[1];
	for(int i=2;i<=k;++i)
	{
		w[i]=w[i-1]+((w[i-1]*2357+137)%10+1);
	}
	
	int l=1,r=w[k],ans=0;
	while(l<=r)
	{
		int mid=(l+r)/2;
		if(check(mid))
		{
			ans=mid;
			l=mid+1;
		}
		else r=mid-1;
	}
	
	cout<<ans;
	return 0;
}

解法二：DP

此题用DP也是可以的，只不过没有二分那么简单，但DP是相当工整的

首先，一维dp是不行的，我们要记录的无非是三种东西：看过的桩子数，选中的个数，以及最大距离，

所以用二维dp

f[i][j]表示看完了i个桩子后选中了j个桩子中距离最近的奶牛之间的最大距离

我们最后是需要得到f[k][n]的值

下面就是要找子任务，俗称“回头望月”

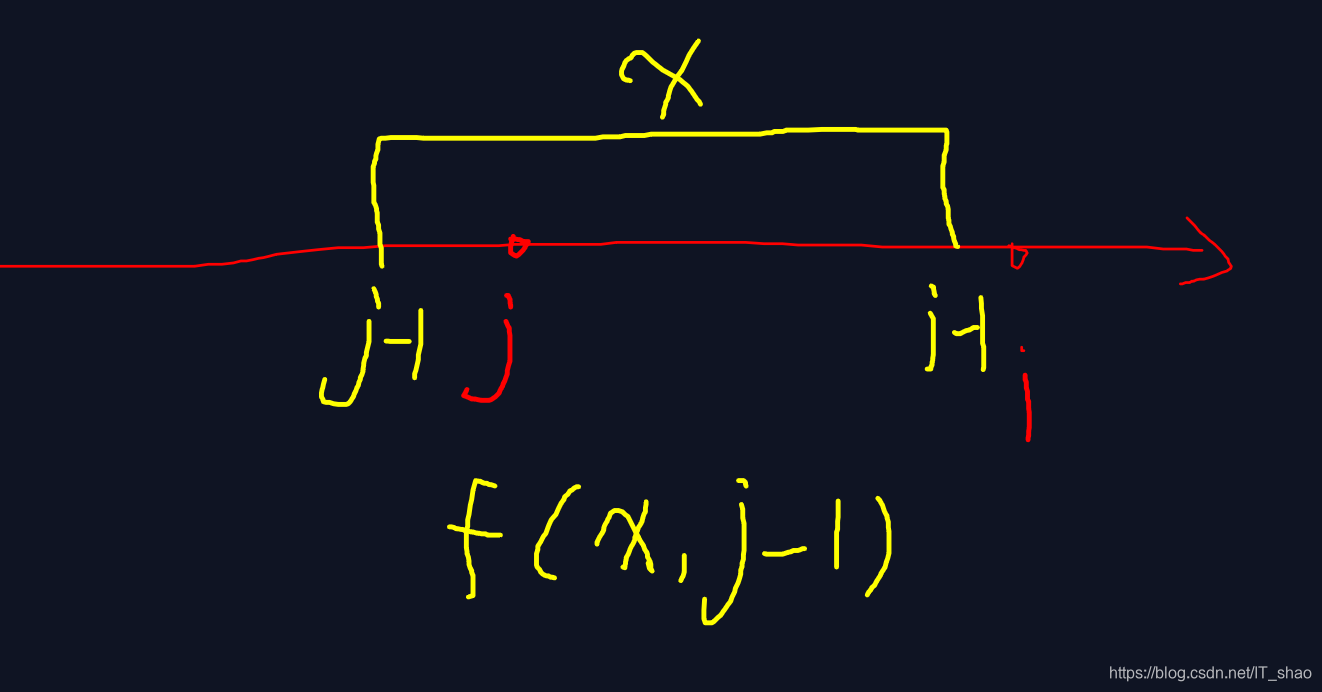
首先我们可以肯定的是他的子问题一定是f[x][j-1]，即看到了x个桩子，选中了j-1个。那么x的范围也很好确定，最大不能超过i-1，因为选中了j-1个，所以最小不能小过j-1（这就是上面这张图）

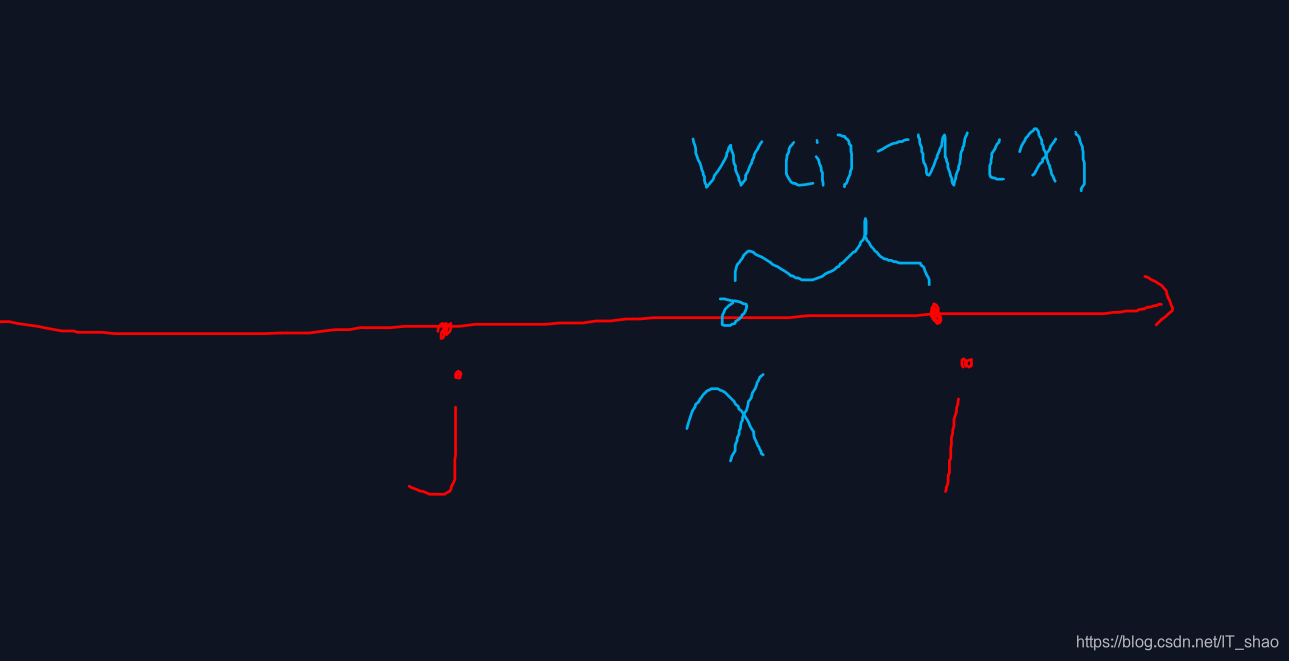
现在我们来看对于每一个x怎么处理？首先明确f[x][j-1]存的是，看到了x个桩子，选中了j个桩子中，最近的奶牛之间间隔的最大值。

那么接下来要更新两个东西：最近的奶牛和他们的最大值

如果w[i]-w[x]<f[x][j-1],那么他就是那个最近的两头奶牛，假设值为minv

那么我们会得到很多个minv，所谓最小值最大，其实就是max_minv

 

Code：

#include <bits/stdc++.h>
using namespace std;
int n,k,w[105];
int f[105][105];


int main()
{
	int maxv,minv;
	cin>>n>>k>>w[1];
	for(int i=2;i<=k;++i)
	{
		w[i]=w[i-1]+((w[i-1]*2357+137)%10+1);
	}
	
	for(int i=1;i<=k;i++)
	 for(int j=1;j<=n;j++)
	  f[i][j]=20000;
	
	for(int i=2;i<=k;i++)
	{
		for(int j=2;j<=i,j<=n;j++)
		{
			maxv=-1;
			for(int x=j-1;x<=i-1;x++)
			{
				minv=min(f[x][j-1],w[i]-w[x]);
				maxv=max(minv,maxv);
			}
			
			f[i][j]=maxv;
		}
	}
	
	cout<<f[k][n]<<endl;
 }