矩阵快速幂——HDU 4565

• 题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4565

• 题意：给出 $a,b,n,m \ 0< a, m < 2^{15}, (a-1)^2< b < a^2, 0 < b, n < 2^{31} \ \ \ $ 求解：
  

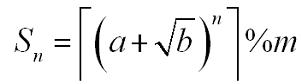
• 分析：直接怼肯定会烂掉，但是好像也没有什么大浮点数的快速幂。我尝试过用java的大浮点数来计算，但还是会崩。但是 爱克赛普特 说过：人的命运啦，都不可预料，当你卡题的时候，请拿起离你最近的一本书看看。我就看了看，就做出来了：

$\because\ (a+\sqrt b\ )^n = x_n + y_n*\sqrt b\ ,\ (a-\sqrt b\ )^n = x_n - y_n*\sqrt b\ $
$\therefore\ (a+\sqrt b\ )^n + (a-\sqrt b\ )^n = 2*x_n$
$\therefore\ (a+\sqrt b\ )^n = 2*x_n- (a-\sqrt b\ )^n$
$\because\ (a-1)^2< b\ < a^2$
$\therefore\ (a+\sqrt b\ )^n = 2*x_n- (a-\sqrt b\ )^n = 2*x_n$

$So\ we\ only\ need\ to\ solve\ the\ x_n,\ and\ we\ can\ find\ that\ :$
$(a+\sqrt b\ )^0 = 1 + 0*\sqrt b\ $
$(a+\sqrt b\ )^1 = a + 1*\sqrt b\ $
$(a+\sqrt b\ )^2 = (a^2+b\ )+2a*\sqrt b\ $
$\therefore\ x_0 = 1, y_0 = 0;\ x_1 = a,y_1=1;\ x_2 = (a^2+b\ ), y_2 = 2a;$
$\therefore\ \begin{bmatrix}x_n\\ y_n\end{bmatrix} = \begin{bmatrix} a & b\ \\ 1 & a\end{bmatrix}^n\times\begin{bmatrix}x_0\\ y_0\end{bmatrix}$

• 所以啊，我们还是要多学习一个。

• AC代码：

/*************************************************************************
    > File Name: test.cpp
    > Author: Akira 
    > Mail: qaq.febr2.qaq@gmail.com 
 ************************************************************************/

#include <iostream>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cstdlib>
#include <algorithm>
#include <bitset>
#include <queue>
#include <stack>
#include <map>
#include <cmath>
#include <vector>
#include <set>
#include <list>
#include <ctime>
#include <climits>
typedef long long LL;
typedef unsigned long long ULL;
typedef long double LD;
#define MST(a,b) memset(a,b,sizeof(a))
#define CLR(a) MST(a,0)
#define Sqr(a) ((a)*(a))
using namespace std;

#define MaxN 100001
#define MaxM MaxN*10
#define INF 0x3f3f3f3f
#define PI 3.1415926535897932384626
LL mod;
const double eps = 1e-6;
#define bug cout<<88888888<<endl;
#define debug(x) cout << #x" = " << x << endl;

const int MatLen = 4;//赋值
//矩阵
struct Mat
{
    LL mat[MatLen][MatLen];
    Mat()  
    {  
        CLR(mat);
    } 
    void init(LL v)  
    {  
        for(int i=0; i<=MatLen; ++i)  
            mat[i][i]=v;  
    } 
};

//矩阵乘法
Mat operator * (Mat a, Mat b)
{
    Mat c;
    for(int k=0;k<MatLen;k++)
    {
        for(int i=0;i<MatLen;i++)
        {
            for(int j=0;j<MatLen;j++)
            {
                c.mat[i][j] += a.mat[i][k]%mod * b.mat[k][j]%mod ;
            }
        }
    }

    return c;
}

//矩阵快速幂
Mat operator^(Mat a, long long int k)
{
    Mat c;
    for(int i=0;i<MatLen;i++)
    {
        for(int j=0;j<MatLen;j++)
        {
            c.mat[i][j] = (i==j);
        }
    }
    for(; k; k>>=1)
    {
        if(k&1)
            c = c*a;
        a = a*a;
    }
    return c;
}
LL n,a,b;
int main()
{
    while(~scanf("%lld%lld%lld%lld", &a, &b, &n, &mod) )
    {
        Mat num;
        num.mat[0][0] = a;
        num.mat[0][1] = b;
        num.mat[1][0] = 1;
        num.mat[1][1] = a;
        Mat ans = num^n;
        LL ANS = 2*ans.mat[0][0]%mod;
        printf("%lld\n", ANS);

    }

}