高斯混合概率假设密度滤波器（GM-PHD）研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

高斯混合概率假设密度滤波器（GM-PHD）研究

这是对高斯混合概率假设密度滤波器（GM-PHD）的实现，该滤波器在以下文献中有描述：

摘要：
针对存在数据关联不确定性、检测不确定性、噪声和误报的情况，提出了一种新的递归算法，用于从一系列观测集中联合估计目标数量和状态的时变情况。该方法涉及将目标和测量的各个集合建模为随机有限集，并应用概率假设密度（PHD）递归来传播后验强度，后验强度是目标随机有限集的一阶统计量。目前，对于PHD递归，尚无闭式解。本文表明，在对目标动态和出生过程进行线性、高斯假设的情况下，任意时间步长处的后验强度是高斯混合的。更重要的是，推导出了传播后验强度的成分高斯组件的均值、协方差和权重的闭式递归。提出的算法将这些递归与一种管理高斯组件数量以提高效率的策略相结合。此算法通过使用扩展卡尔曼滤波器和无迹卡尔曼滤波器中的近似策略，扩展以适应轻微非线性的目标动态。

GM-PHD滤波器是一种用于估计测量数据中目标数量和位置的方法。其优点包括表示目标位置不确定性（使用协方差矩阵）以及目标存在不确定性（使用权重），并且在更新步骤中不存在数据关联。这个实现进行了相当详细的注释，可能对试图了解GM-PHD滤波的人会很有帮助，但是Vo＆Ma的论文是理解实际情况的关键。

模拟器在杂波环境中创建两个移动目标的嘈杂测量数据，大约在模拟的中间阶段创建第三个目标。这是一个相当简单的问题，但它有效地演示了滤波器的性能。Vo＆Ma用它来演示线性GM-PHD滤波器，但我也用它来演示EKF版本，而不是编码他们描述的EKF模拟器。
这对于GM-PHD滤波器的工作并不是必需的，但提供了一种很好的可视化和量化性能的方式。如果人们想要调整这段代码，该度量是观察性能如何的一种很好的方式，并且可以相对容易地修改这个实现，以使用相同的数据执行多个测试运行，但使用不同的滤波器参数并比较度量。

错差（或称为误差）的概念，在任何过滤/控制问题中都起着基础性的作用，它表示参考量与其估计/控制值之间的差异。然而，在已经建立的多目标过滤领域中，尚无对错差的令人满意的概念。在本文中，我们概述了现有度量标准在多目标错差方面的不一致性，用于性能评估。然后，我们提出了一种新的在数学上和直观上都一致的度量标准，以解决当前多目标性能评估度量标准的缺点。

一、引言

多目标跟踪是信息融合领域的重要研究方向，旨在复杂环境中对多个目标的运动状态进行实时估计和轨迹管理。传统方法如联合概率数据关联（JPDA）和多假设跟踪（MHT）在处理大量目标时面临计算复杂度高、难以实时应用的挑战。基于随机有限集（RFS）理论的高斯混合概率假设密度（GM-PHD）滤波器为多目标跟踪提供了新解决方案，通过递推估计多目标后验概率假设密度（PHD），实现了对目标数量和状态的联合估计。

二、GM-PHD滤波器的理论基础

1. 随机有限集（RFS）理论
   RFS理论将多目标状态空间和多目标量测空间均建模为随机有限集，其中每个元素代表一个目标的状态向量或传感器的量测向量。PHD函数定义为多目标后验RFS的期望，其在任意状态空间子集上的积分等于该子集中目标的期望数量。PHD滤波器通过递推更新PHD函数来估计多目标状态，避免了传统方法中复杂的量测与目标关联问题。

2. 高斯混合近似
   原始PHD滤波器在预测和更新过程中通常无法获得解析解。为解决这一问题，GM-PHD滤波器引入高斯混合近似，假设PHD可表示为有限个高斯分量的加权和。每个高斯分量代表一个潜在目标的概率分布，其均值和协方差分别表示目标状态的估计和不确定性，权重反映目标存在的概率。

三、GM-PHD滤波器的算法实现

1. 初始化
   根据先验知识或首次检测到的目标信息，设置初始高斯分量集，包括每个高斯分量的权重、均值和协方差。

2. 预测步
   每个高斯分量根据目标运动模型进行预测。对于线性高斯系统，预测后的高斯分量仍为高斯分布，其均值和协方差通过状态转移矩阵和过程噪声协方差矩阵更新，权重根据目标存活概率调整。

3. 更新步
   利用当前量测信息修正预测的PHD。对于每个量测，生成一组新的高斯分量，表示量测与现有目标关联的可能性及新目标的产生。更新后的PHD是所有预测高斯分量和由量测生成的新高斯分量的加权和。具体而言，对每个预测高斯分量和每个量测，计算似然函数表示量测来自目标的概率，并根据似然函数和目标检测概率更新高斯分量的权重、均值和协方差。

4. 剪枝与合并
   递推过程中高斯分量数量可能呈指数级增长，导致计算负担过重。通过移除权重低于预设阈值的高斯分量（代表目标存在概率较低的假设），以及合并距离较近且协方差相似的高斯分量（减少高斯分量数量），平衡计算效率和跟踪精度。合并后的新高斯分量的权重、均值和协方差由被合并的高斯分量加权平均得到。

5. 目标状态估计
   在每个时间步，通过对PHD进行聚类或提取权重较大的高斯分量的均值，得到目标数量和每个目标的状态估计。

四、GM-PHD滤波器的性能优势

1. 简化算法设计
   GM-PHD滤波器直接估计多目标PHD，避免了复杂的量测与目标关联问题，降低了计算复杂度。

2. 自适应处理目标动态变化
   能够同时估计目标数量和目标状态，无需预设目标数量，可自适应处理目标的出现和消失。

3. 鲁棒性
   在理论上能更好地处理杂波和漏检，因为它们被自然地融入到PHD的更新过程中。

4. 实时性
   相较于MHT等方法，GM-PHD滤波器的计算复杂度更低，尤其在目标数量较多时，更容易实现实时应用。

五、GM-PHD滤波器在不同应用场景中的研究进展

1. 雷达目标跟踪
   GM-PHD滤波器被用于处理强杂波、多目标、目标新生和消亡等复杂场景，并取得了良好的跟踪性能。研究方向包括改进量测模型、融合多源信息等。

2. 视频监控
   可用于行人跟踪、车辆跟踪等，有效应对遮挡、光照变化、目标频繁进出视野等挑战。研究热点包括与图像处理技术的结合、复杂场景下的鲁棒性提升等。

3. 机器人SLAM和多机器人协同定位
   可同时估计多个未知环境特征点或多个机器人的状态，提高系统在复杂环境中的感知能力。

4. 无线传感器网络
   可用于分布式多目标跟踪，通过融合来自不同传感器的局部信息，实现对目标全局状态的估计。

5. 生物医学领域
   被应用于细胞跟踪、微生物种群密度估计等，为生物现象的研究提供了新的工具。

六、GM-PHD滤波器的局限性与未来展望

1. 非线性问题
   当目标运动模型或量测模型存在严重的非线性时，高斯近似可能不再准确，导致性能下降。未来研究可探索更精确的PHD近似方法，如粒子PHD（Particle PHD）或基于蒙特卡洛采样的PHD滤波器。

2. 剪枝与合并策略优化
   当前的剪枝与合并策略基于启发式规则，如何设计更优的策略以在计算效率和跟踪精度之间取得更好的平衡是一个持续的研究方向。

3. 扩展目标和群目标跟踪
   传统的GM-PHD滤波器主要针对点目标，对于扩展目标（即目标尺寸不可忽略）或群目标（即多个目标作为一个整体运动）的跟踪能力有限。未来研究将致力于开发适用于扩展目标和群目标的GM-PHD变种。

📚2 运行结果

2.1 GM-PHD滤波器，不包含扩展卡尔曼滤波器EKF

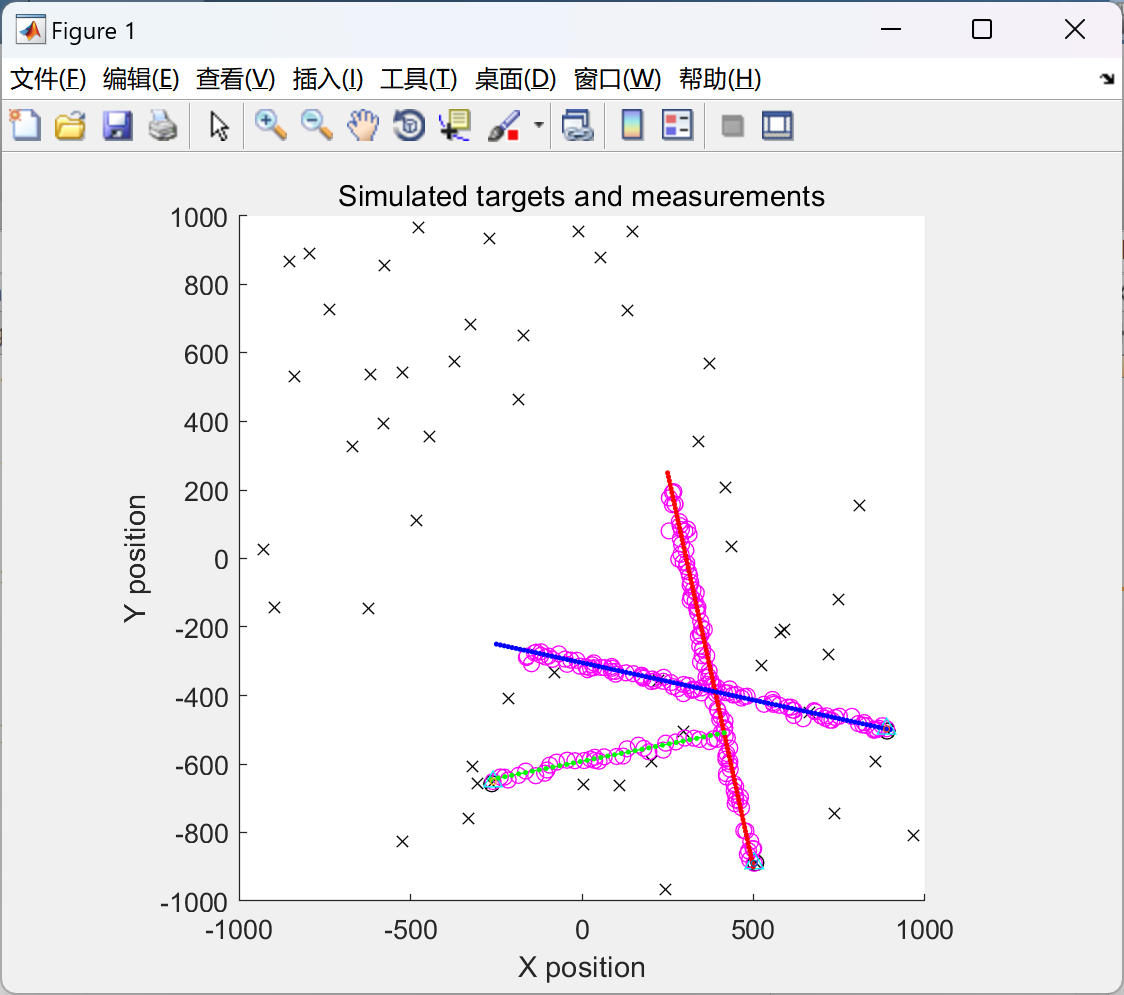
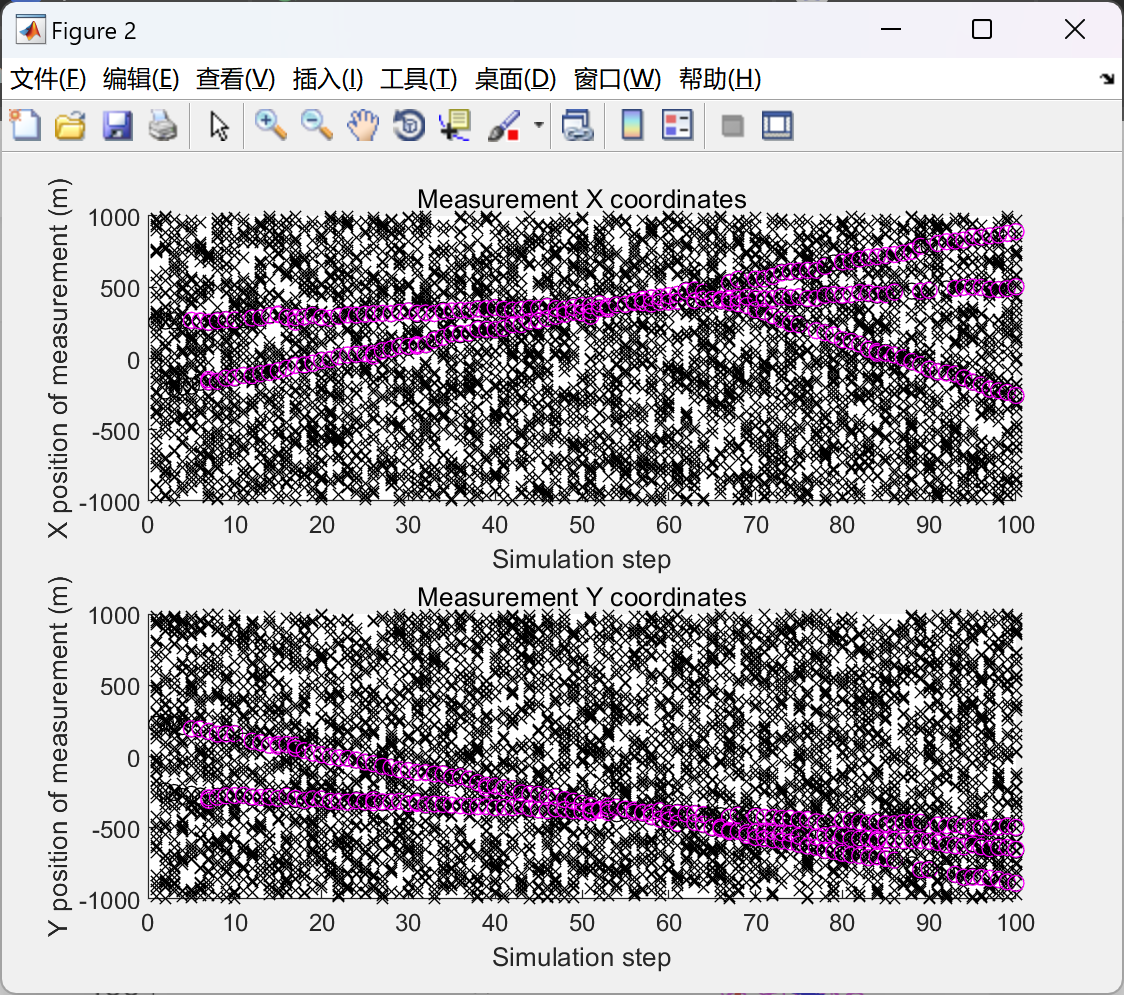
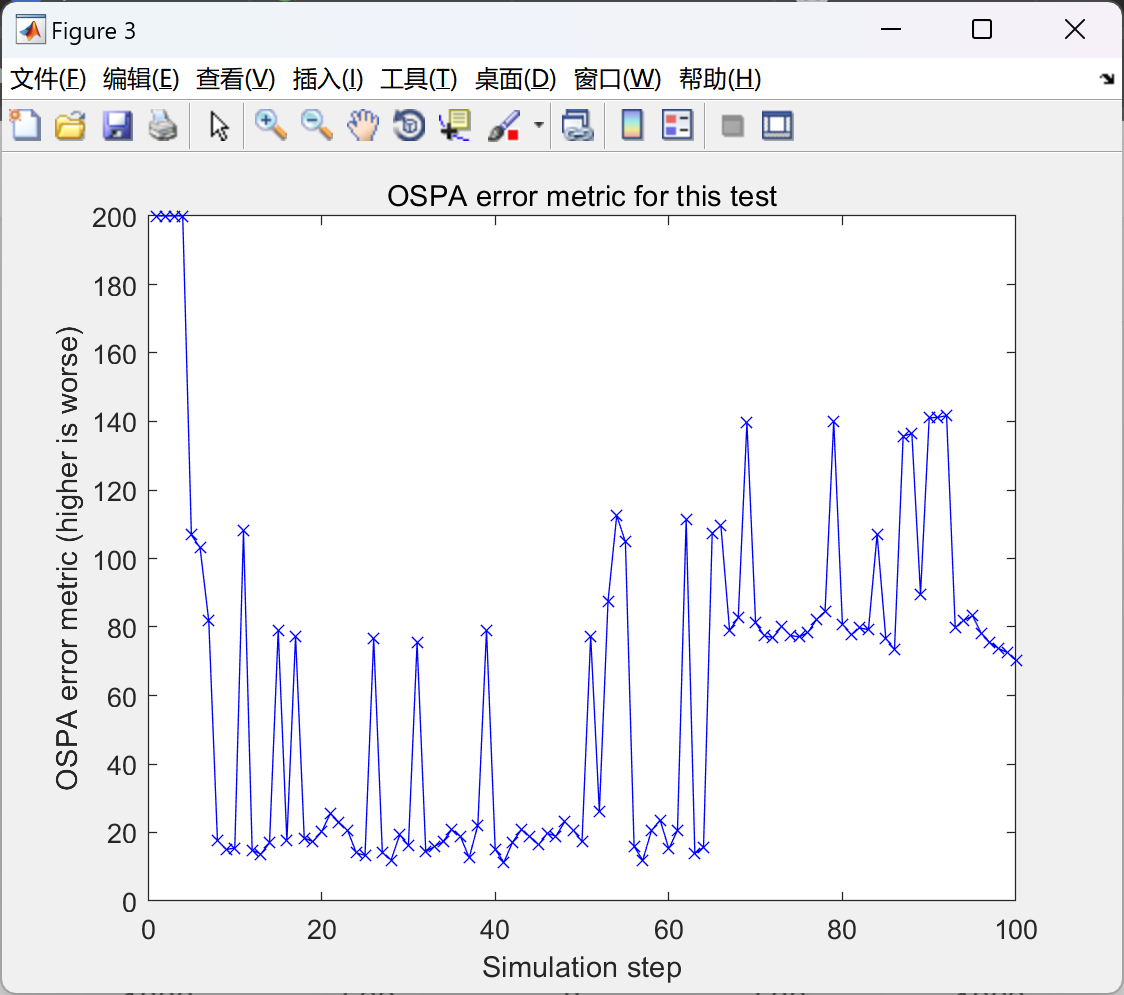
2.2 GM-PHD滤波器，包含扩展卡尔曼滤波器EKF

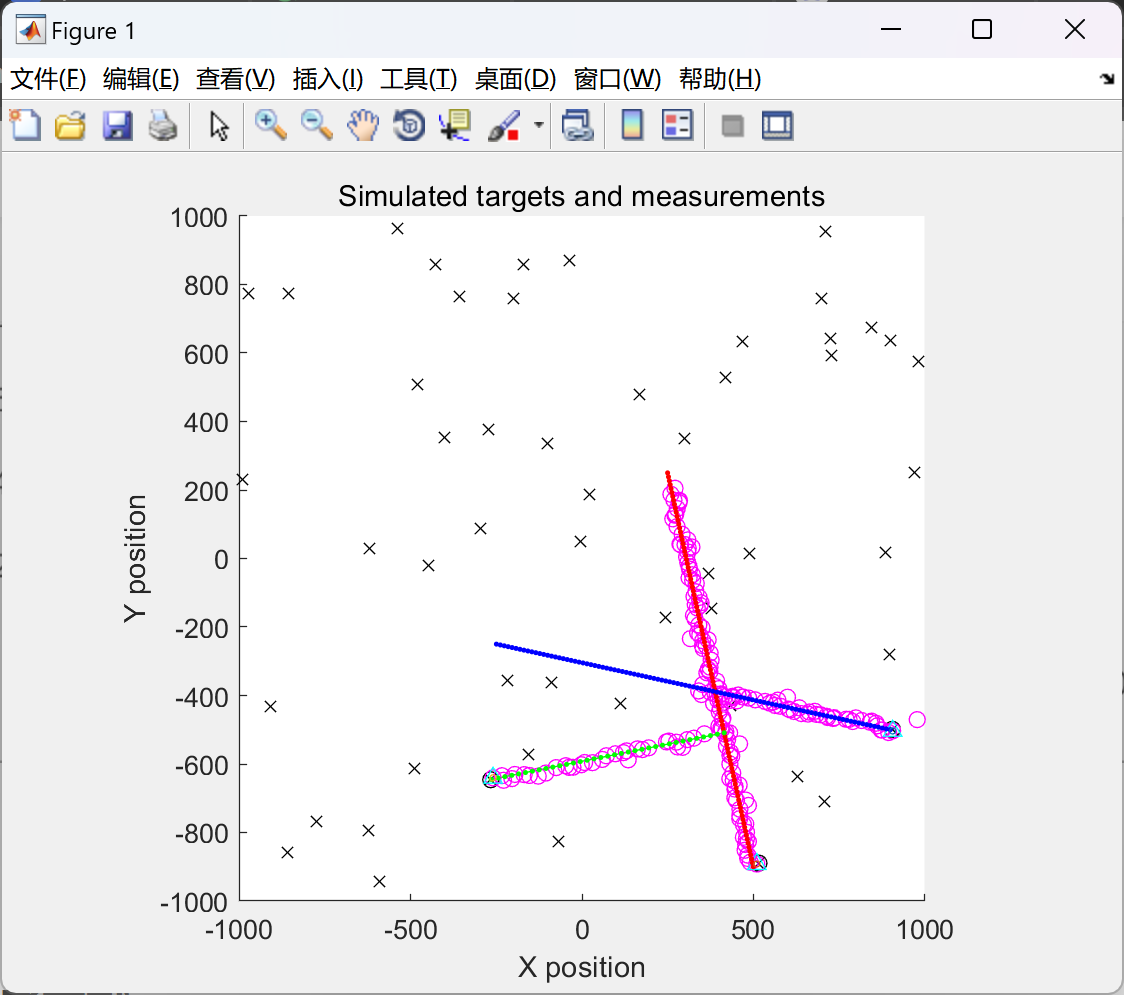
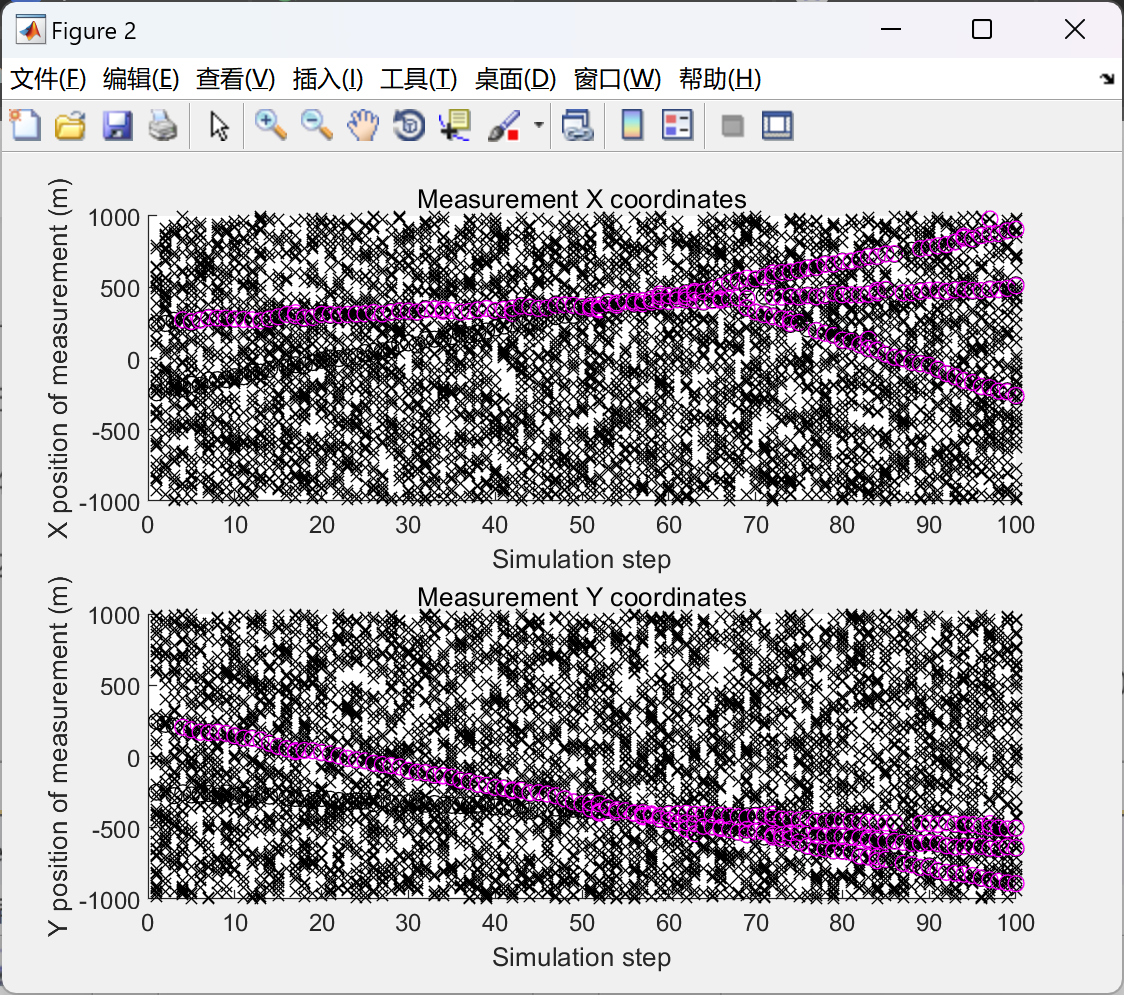
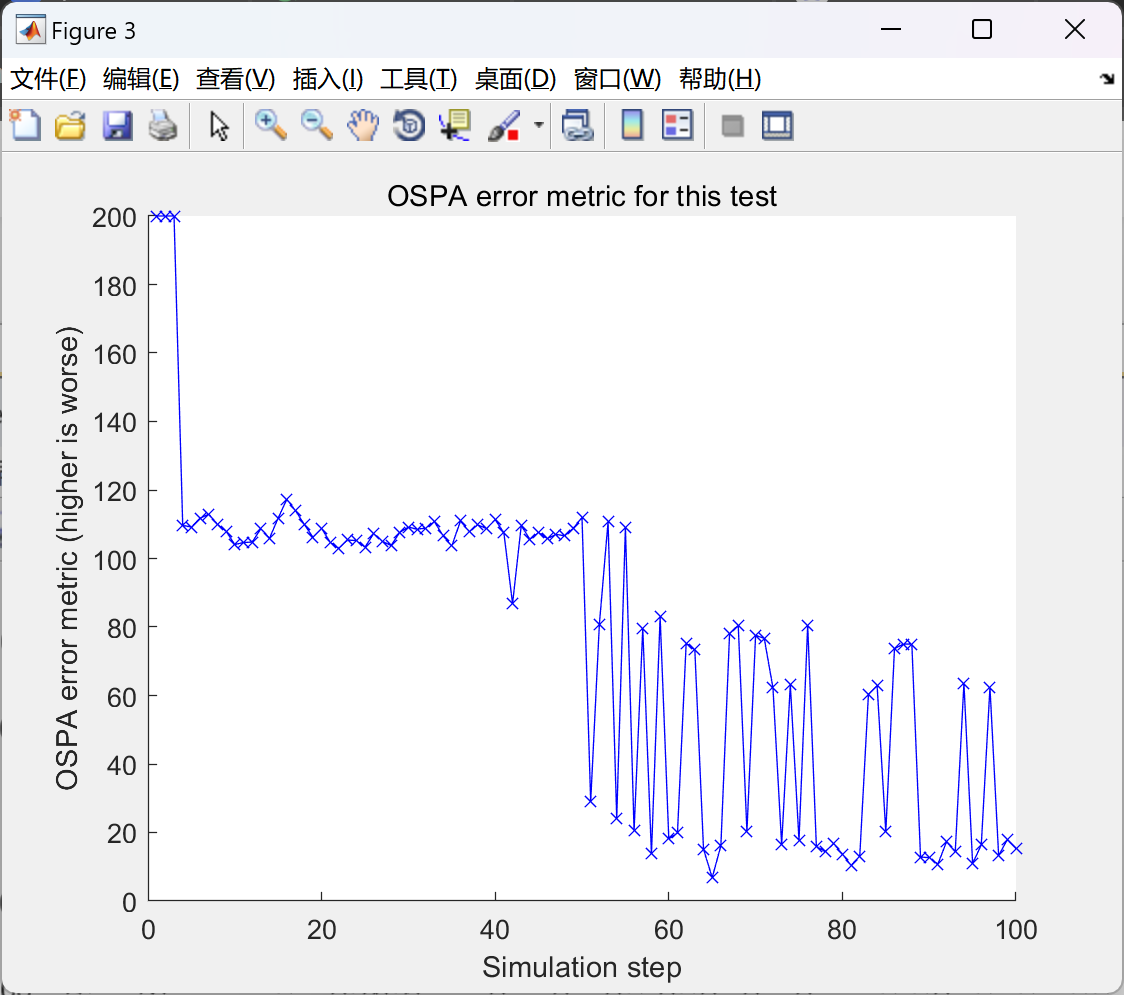
部分代码：

 %Step Sim: Generate sensor Measurements
    %If you want to use this code with your own data or for a different problem,
    %replace this function with your own.
    if USE_EKF == 0
        GM_PHD_Simulate_Measurements;  %Linear KF measurements are simulated direct observations [X; Y] of the target positions
    else
        GM_EKF_PHD_Simulate_Measurements; %EKF measurements are simuated range-bearing [r; theta] of the target position from a fixed sensor.
    end
    
    %Linear KF use fixed matrices for prediction and update.
    %EKF calculates Jacobians to linearise the prediction and observation
    %models. There is need for an inverse sensor model to map from sensor
    %to target space for some calculations.
    if(USE_EKF == 0)
        %Step 1: Prediction for birthed/spawned targets 
        GM_PHD_Predict_Birth; 
        %Step 2: Prediction for existing targets
        GM_PHD_Predict_Existing;
        %Step 3: Construction of PHD update components
        GM_PHD_Construct_Update_Components;
        %Step 4: Update targets with measurements
        GM_PHD_Update;
    else
        %Step 1: Prediction for birthed/spawned targets 
        GM_EKF_PHD_Predict_Birth; %EKF prediction uses Jacobians to linearise the prediction model and predict the targets forward in time
        %Step 2: Prediction for existing targets
        GM_EKF_PHD_Predict_Existing;
        %Step 3: Construction of PHD update components
        GM_EKF_PHD_Construct_Update_Components;
        %Step 4: Update targets with measurements
        GM_EKF_PHD_Update;
    end
    
    %Step 5: Prune targets
    GM_PHD_Prune;
    %Step 6: Estimate position of targets
    GM_PHD_Estimate

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]B.-N. Vo, W.-K. Ma, "The Gaussian Mixture Probability Hypothesis Density Filter", IEEE Transactions on Signal Processing, Vol 54, No. 11, November 2006, pp4091-4104.

[2]Schuhmacher, D.; Ba-Tuong Vo; Ba-Ngu Vo, "A Consistent Metric for Performance Evaluation of Multi-Object Filters," Signal Processing, IEEE Transactions on , vol.56, no.8, pp.3447,3457, Aug. 2008.

🌈4 Matlab代码、数据、文章