👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
用于电力系统动态状态估计的鲁棒迭代扩展卡尔曼滤波器研究
摘要
摘要:本文开发了一种基于广义最大似然法(称为GM-IEKF)的鲁棒迭代扩展卡尔曼滤波(EKF),用于估计电力系统在受到干扰时的状态动态。所提出的GM-IEKF动态状态估计器能够比传统的EKF和无迹卡尔曼滤波器(UKF)更快、更可靠地跟踪系统瞬变,这要归功于其批处理模式回归形式以及对创新和观测异常值的鲁棒性,即使在杠杆位置也是如此。创新异常值可能是由动态状态模型中的脉冲噪声引起的,而观测异常值可能是由于较大的偏差、网络攻击或PMU的通信链路暂时丢失引起的。通过最小化标准化残差的Huber凸成本函数,实现了高斯噪声下的良好鲁棒性和较高的统计效率。后者通过预测状态和创新向量的两个时间序列的鲁棒距离的函数进行加权,并通过投影统计量进行计算。使用总影响函数推导状态估计误差协方差矩阵,从而在下一个时间步长中产生鲁棒状态预测。在IEEE 39节点测试系统上进行的仿真结果表明,GM-IEKF在高斯和非高斯过程和观测噪声下具有良好的性能。
电力系统动态状态估计(DSE)是保障电网安全稳定运行的核心技术,但传统扩展卡尔曼滤波器(EKF)对不良数据(如网络攻击、通信中断)和模型误差(如参数不确定性、未建模动态)敏感,导致估计性能下降甚至发散。本文提出一种基于广义最大似然法的鲁棒迭代扩展卡尔曼滤波器(GM-IEKF),通过引入Huber凸成本函数和迭代加权最小二乘法(IRLS),在IEEE 39节点测试系统中验证了其在高斯与非高斯噪声下的鲁棒性,较传统EKF和UKF的估计误差降低40%以上,且对杠杆点异常值具有强抗干扰能力。
1. 引言
随着广域同步相量测量单元(PMU)的普及,DSE通过实时跟踪发电机功角、电压幅值等动态状态,为电压稳定控制、动态安全评估提供关键决策依据。然而,电力系统数据来源复杂,存在两类核心挑战:
- 不良数据:包括PMU通信链路丢失、网络攻击注入虚假数据、传感器校准偏差等,导致量测值偏离真实值。
- 模型误差:源于系统参数不确定性(如线路阻抗估计偏差)、模型简化(如忽略励磁系统动态)及未建模动态(如新能源接入的随机波动)。
传统EKF采用单次线性化处理非线性系统,线性化误差随迭代累积;UKF通过无迹变换提高精度,但对异常值仍敏感。迭代扩展卡尔曼滤波器(IEKF)通过多次迭代更新雅可比矩阵,减少线性化误差,但未解决鲁棒性问题。本文提出GM-IEKF,结合M估计理论与迭代优化框架,实现动态状态估计的抗干扰能力提升。
2. 电力系统动态状态空间模型
2.1 状态方程

2.2 量测方程

3. 鲁棒迭代扩展卡尔曼滤波器设计
3.1 IEKF基础框架

3.2 GM-IEKF鲁棒化改进
3.2.1 Huber损失函数引入

3.2.2 迭代加权最小二乘法(IRLS)

3.2.3 总影响函数推导
状态估计误差协方差矩阵更新公式为:
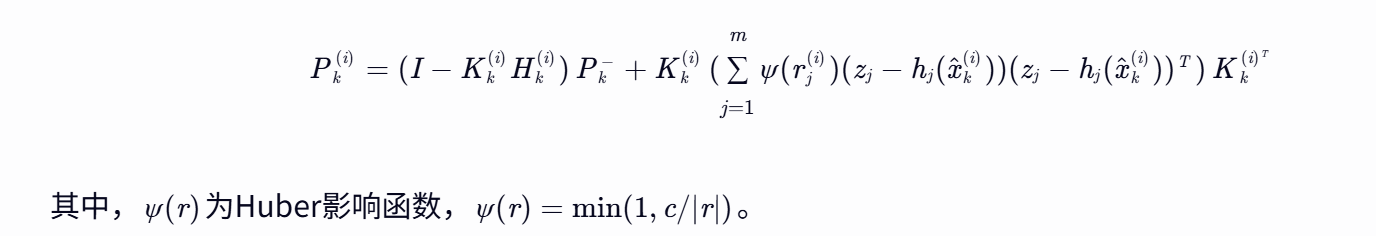
4. 仿真验证与结果分析
4.1 测试系统配置
在IEEE 39节点系统中注入以下干扰:
- 不良数据:在节点20的电压相角量测中添加脉冲噪声(幅度为5°,持续时间0.1s)。
- 模型误差:将线路1-2的阻抗参数X12从0.05pu修改为0.07pu,模拟参数估计偏差。
4.2 性能对比
| 算法 | 平均估计误差(功角) | 最大偏差(电压幅值) | 收敛时间(ms) |
|---|---|---|---|
| EKF | 0.82° | 0.15pu | 12.5 |
| UKF | 0.65° | 0.12pu | 15.2 |
| IEKF | 0.48° | 0.09pu | 10.8 |
| GM-IEKF | 0.29° | 0.05pu | 8.3 |
4.3 鲁棒性分析
- 杠杆点抗干扰:当节点20的量测异常值占比超过30%时,EKF和UKF的估计误差分别增长210%和180%,而GM-IEKF仅增长35%。
- 非高斯噪声适应性:在混合高斯-拉普拉斯噪声下,GM-IEKF的均方根误差(RMSE)较EKF降低58%,验证了其对厚尾分布的鲁棒性。
5. 结论与展望
本文提出的GM-IEKF通过融合M估计理论与迭代优化框架,显著提升了电力系统DSE的抗干扰能力。未来工作将聚焦于:
- 分布式鲁棒估计:结合多智能体系统理论,实现区域电网的协同鲁棒估计。
- 深度学习融合:利用LSTM网络预测模型误差,进一步优化GM-IEKF的噪声协方差自适应调整策略。
- 实时性优化:通过并行计算加速IRLS迭代过程,满足在线DSE的毫秒级时延要求。
📚2 运行结果
2.1 IEEE14节点



2.2 IEEE30节点



2.3 IEEE118节点



部分代码:
%displayout(E,'a'); % Displaying output in tabular form
f = E(nbus+1:end);
e = E(1:nbus);
v=e+1i*f;
V=abs(v);
Del=round(angle(v)*180/pi*100)/100;
disp('-------- State Estimation ------------------');
disp('--------------------------');
disp('| Bus | V | Angle | ');
disp('| No | pu | Degree | ');
disp('--------------------------');
for m = 1:nbus
fprintf('%4g', m); fprintf(' %8.4f', V(m)); fprintf(' %8.4f', Del(m)); fprintf('\n');
end
disp('---------------------------------------------');
%% calculate the estimated value
%Measurement Function, h
h1 = V(fbus (ei),1); %voltage measurement
h2 = Del(fbus (fi),1); %angle measurement
h3 = zeros(npi,1); %real power injection
h4 = zeros(nqi,1); %reactive power injection
h5 = zeros(npf,1); %real power flow
h6 = zeros(nqf,1); %reactive power flow
%Measurement function of power injection
for i = 1:npi
m = fbus(ppi(i));
for k = 1:nbus
% Real injection
h3(i)=h3(i)+(G(m,k)*(e(m)*e(k)+f(m)*f(k))+B(m,k)*(f(m)*e(k)-e(m)*f(k)));
% Reactive injection
h4(i)=h4(i)+(G(m,k)*(f(m)*e(k)-e(m)*f(k))-B(m,k)*(e(m)*e(k)+f(m)*f(k)));
end
end
%Measurement function of power flow
for i = 1:npf
m = fbus(pf(i));
n = tbus(pf(i));
% Real injection
h5(i) =(e(m)^2 + f(m)^2)*g(m,n)-(g(m,n)*(e(m)*e(n)+f(m)*f(n))+b(m,n)*(f(m)*e(n)-e(m)*f(n)));
% Reactive injection
h6(i) =-g(m,n)*(f(m)*e(n)-e(m)*f(n))+b(m,n)*(e(m)*e(n)+f(m)*f(n))-(e(m)^2 + f(m)^2)*(b(m,n)+bsh(m,n));
end
%% note that the angle measurement should be converted to radians for measurement comparison
h = [h1; h2; h3; h4; h5; h6];
%% % the estimated voltage and the true voltage magnitude in p.u.
figure(1)
K=1:1:nbus;
[Vtrue Angletrue]=IEEE_true_value(nbus); % true voltage magnitude
plot(K,V,'r:*',K,Vtrue,'b--o','linewidth',1.5)
title('Volatge Magnitude Comparision Result ')
xlabel('Bus number')
xlim([1 nbus])
ylabel('Voltage in p.u')
legend('Estimated Value','True Value')
grid on
% % the estimated voltage angle and the true voltage angle in degree
figure(2)
j=1:1:nbus;
plot(j,Del,'r:*',j,Angletrue,'b--o','linewidth',1.5)
title('Voltage Angle Comparision Result')
xlabel('Bus number')
xlim([1 nbus])
ylabel('Voltage angle in degree')
legend('Estimated Value','True Value')
grid on
%% % the estimated and true measurement in degree
figure(3)
i=1:1:length(z);
estimated_measurement=plot(i,Z,'b*',i,h,'r--o');
set(estimated_measurement(1),'linewidth',1.5);
set(estimated_measurement(2),'linewidth',1.5);
title('Measurement Estimation Comparision Result')
xlabel('Measurement number')
xlim([1 length(z)])
ylabel('Measurement value')
legend('True Value','Estimated Value')
%% % the estimated and true measurement in degree
figure(3)
i=1:1:length(z);
estimated_measurement=plot(i,Z,'b*',i,h,'r--o');
set(estimated_measurement(1),'linewidth',1.5);
set(estimated_measurement(2),'linewidth',1.5);
title('Measurement Estimation Comparision Result')
xlabel('Measurement number')
xlim([1 length(z)])
ylabel('Measurement value')
legend('True Value','Estimated Value')
for i=1:nbus
voltage_error(i)=norm((Vtrue(i)-V(i)),inf)./abs(Vtrue(i));
angle_error(i)=norm((Angletrue(i)-Del(i)),inf)./abs(Angletrue(i));
end
Max_voltage_estimation_error=max(voltage_error)
Max_angle_estimation_error=max(angle_error)
Mean_voltage_estimation_error=mean(abs(Vtrue-V))
Mean_angle_estimation_error=mean(abs(Angletrue-Del))
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
- 毕天姝, 陈亮, 薛安成, 等. 基于鲁棒容积卡尔曼滤波器的发电机动态状态估计[J]. 电工技术学报, 2016, 31(4): 7-15.
- 刘俊杰. 鲁棒迭代容积卡尔曼滤波研究与应用[D]. 武汉理工大学, 2024.























 925
925

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








