机器学习基石第十周笔记

一.Logistic Regression Problem
我们之前讲解的二元分类只是判定输入是与不是，如下：

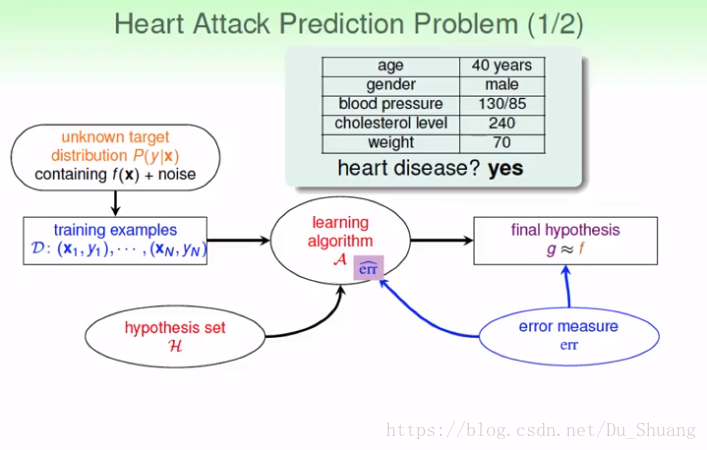
但是我们现在不止想知道是与不是，而是想知道是的几率和不是的几率，那我们该怎么办呢？这时我们就用到了逻逻辑斯回归（我们称之为软分类）：

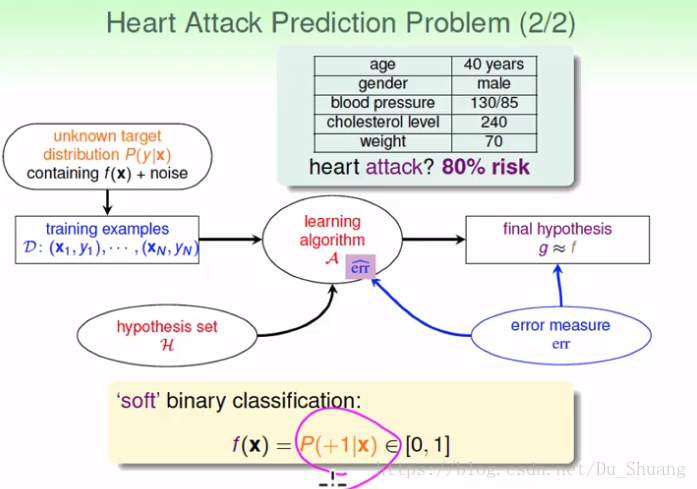
我们要想学得上述所说的东西，那么我们学习所需要的资料应该如下图左边所示（虽然标注为nioseless,其实我们知道我们的学习数据都是有noise的，这里的noiseless只是相对于右边），但是我们只有右边有杂讯的学习资料（我们把右边的学习资料归因为左边的加上杂讯所得到的的资料）

有了学习资料，我们还需要假设空间。
我们将输入数据的加权和作为该输入的分数，该分数越高我们就认为该数据的输出越接近1。然后我们用逻辑函数将该分数归一化到0，1之间，最后得到的结果就是我们的预测概率。

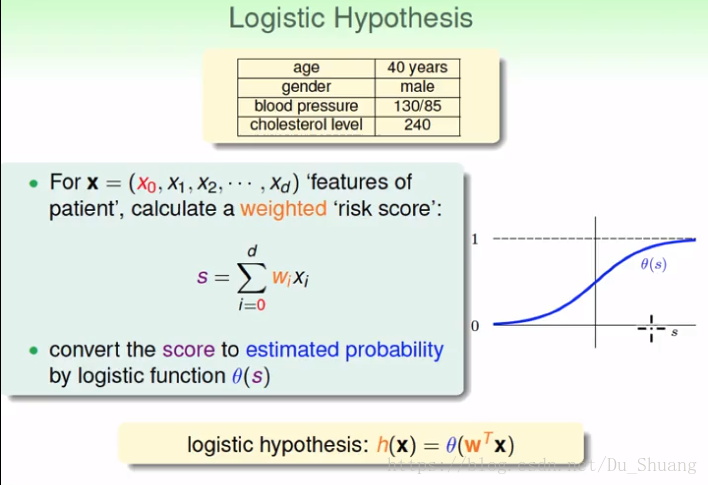
我们使用的逻辑函数性质如下：

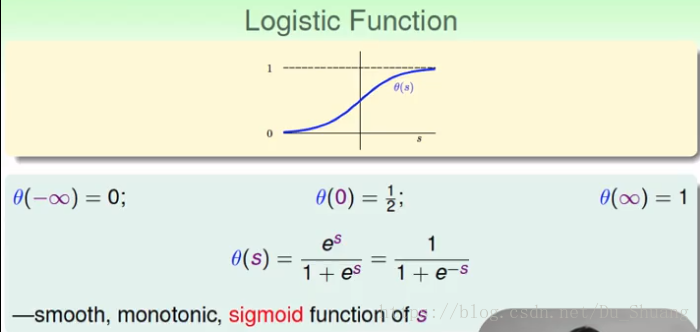
二.Logistic Regression Error
有了假设空间后，我们就需要一个错误函数帮助我们从H中选取一个好的h，我们先将我们之前讲述的两个错误函数通过图像的方式给出来：

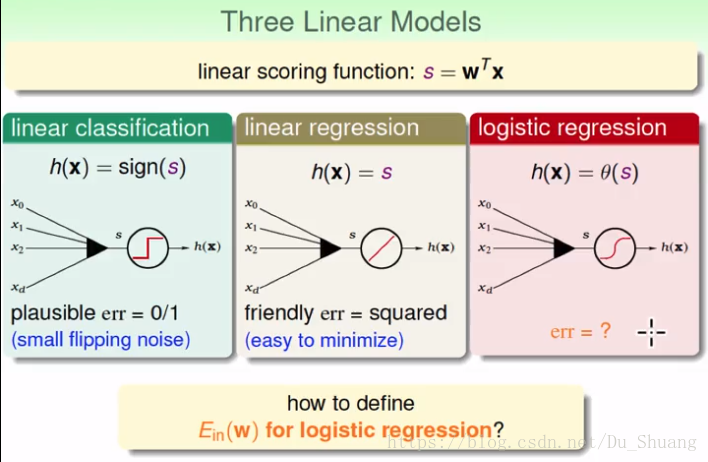
我们的目标函数f(x)估算的结果为P(+1|X)即给定X其为1的概率，反过来我们就能得到一个P(y|x)的分段函数，我们用f(x)产生我们学习数据的概率如下图中左部分所示，P(x1)f(x1)为第一个数据为x1且其y为1的概率，P(x2)(1-f(x2))为第二个数据为X2且其y为0的概率，x1.x2…..xN相互独立，其乘积就是获取整个学习数据D的概率，我们用假设空间的h(x)同样对输入X产生一组和输入空间相同的数据这时我们通过同样的计算也获取了获得该数据的概率，如果这两个概率很接近，那么我们就有理由说h(x)就是f(x)。
那么我们怎么才能判定他们的概率接近呢？由于数据集合D是真实存在的且其是由f(x)采样产生的，所以由f(x)采样产生D的概率最大，我们我们认为h(x)采样获取D的概率越大越接近f(x).

接下来我们要做的就是求出h(x)获取D的概率了，根据逻辑函数的性质我们得到下图的式子：
由于P(xi)概率都一样相当于常数，我们于是将P(xi)提出并用yn对Xi进行正负号的标记

我们得到如下式子：

然后将h(x)替换成其θ（ynW(T)Xn）即变成w的函数，因为我们最后要求的就是w。

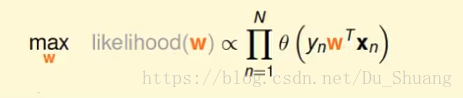
然后为了方便求导我们对式子取Ln(不影响最终结果)将连乘变为连加，为了方便求解凸函数我们将式子反号并且将max变为min，同时将式子除了N（不影响结果），最后如下：

三.Gradient of Logistic Regression
上面求出了错误函数，那么下一步就是想办法让上述的错误函数最小求出我们的g了，我们发现错误函数是个凸函数所以我们能够通过求导等于0的方法求出我们要的那么最小错误所对应的W值。

我们首先对Wi即W向量的单个数据进行求导，然后推出对W的求导，下图的Xn,i代表Xn的第i个元素。最后的Xn为一个向量，每个向量只有一个元素即Xn,i.

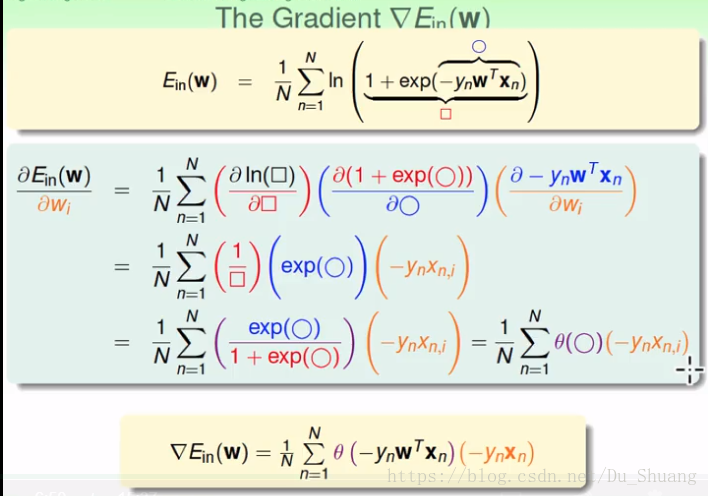
我们令导数等于0，我们发现导数为θ函数的加权和，权值为(-YnXn)，Ein(W)等于0的一种情况是θ函数全等于0，这就意味着θ的变量是一个负无穷大即YnW(T)Xn全部大于0即所有数据都线型可分，但是这经常是不可能的，所以情况只能是加权和为0。但是这里我们又不能像之前线型回归一样有闭式解，直接一步到位，搜哟我们只能参考PLA的求解形式即一步步对结果进行修正。

接下来我们回顾下PLA的求解方式：



四.Gradient Descent
接下来就介绍我们熟悉的梯度下降法了
我觉得这里讲的比其他地方的好很多
根据PLA的姐姐方法，我的的求解方程应为
W(t+1)<——Wt+nV;
这里的V为纠正错误的某个向量我们要求其模为1，n是每次更新的幅度。
这里的物理意义就是朝着正确的方向改变W从而使Ein不断的向谷底的方向接近。

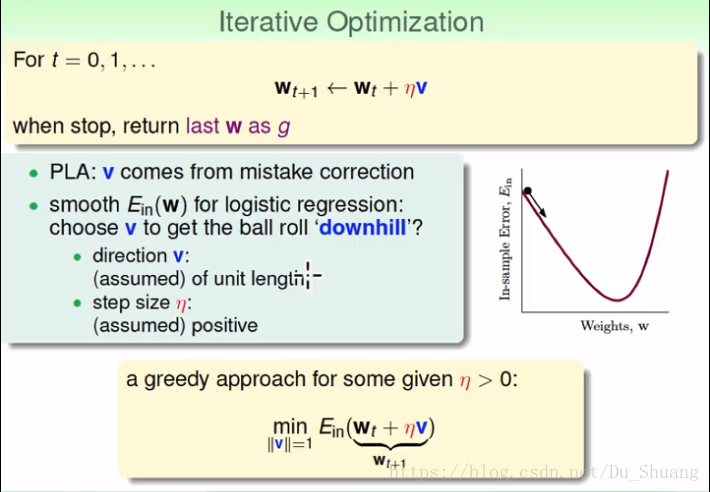
上面的想法虽然很好但是奈何我们不知道这个V到底是什么，所以现在我们的关键是求V。
我们令nV很小然后再Wt处进行一阶泰勒展开，得到如下的公式。

我们现在要做的就是让在每次更新后Ein会变小。
我们要让Ein(Wt)加上后面的那一项后变小，那么V与δEin(Wt)的方向必须反向，因为只有反向的两个向量的乘积才是负数。又因为我们规定V必须是单位向量，所以得到V如下。

接下来我们要做的就是决定η的大小，就是我们每次更新的幅度。
如果我们的η太小，那么每次更新会很慢，就得花费额外的很多时间，如果η很大，那么每次跨太大步，就会把最佳的低点跨过去，那么就会在谷底附近形成震荡，所以我们希望当距谷底远时η大些，当离谷底近了η就小点，所以η与梯度成正比。

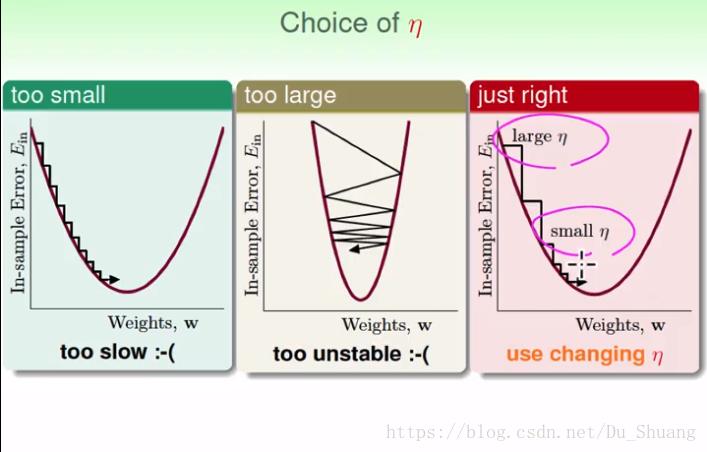
我们将η与梯度的比值定为一个常数计做紫色的η带入原式就得到了下图所示的最终算式。


上述算法步骤总结如下：