EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计。
每次迭代分两部:E步求期望,M步求极大
9.1 EM算法的引入
概率模型既含有观测变量,又含有隐变量或潜在变量。只有观测变量可以使用极大似然估计法,当含有隐变量时就要使用EM法:隐变量的极大似然估计
9.1.1 EM算法
例:三硬币模型

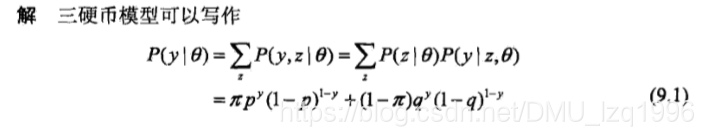
y是观测变量,取值1或0;
z是隐变量,表示A的结果(不可见)
0是模型参数:π,p,q
根据极大似然原理:

求解上面问题,采用迭代方法,即EM算法
1,选取初值:

2,E步
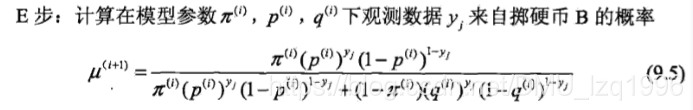
3,M步

注:不同的初值可能得到不同的参数估计
完全数据与不完全数据:

EM算法:


Q函数:

9.1.2 EM算法的推导
极大化观测数据:

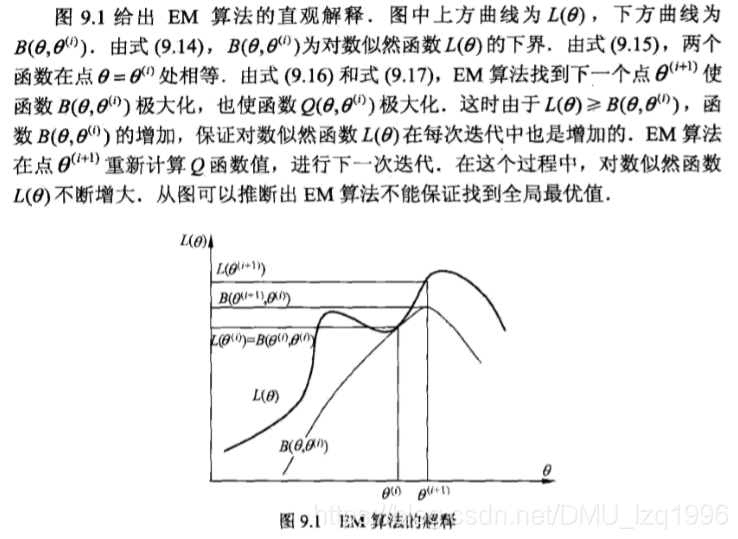
EM算法是通过迭代逐步近似极大化似然函数,是不断求解下界的极大化逼近求解对数似然函数极大化。








 本文深入探讨了EM算法,一种用于含有隐变量的概率模型参数极大似然估计的迭代算法。通过实例讲解,介绍了算法的工作原理,包括E步求期望与M步求极大化的过程,并讨论了不同初值对参数估计的影响。
本文深入探讨了EM算法,一种用于含有隐变量的概率模型参数极大似然估计的迭代算法。通过实例讲解,介绍了算法的工作原理,包括E步求期望与M步求极大化的过程,并讨论了不同初值对参数估计的影响。
















 339
339

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








