插补周期对于运动控制精度的影响的验证

最新推荐文章于 2025-12-05 03:27:21 发布

原创最新推荐文章于 2025-12-05 03:27:21 发布 · 2.4k 阅读

8 ·

CC 4.0 BY-SA版权

本文探讨了圆弧插补的实现过程，通过调整插补周期中的运动间隔interval，研究其对插补轨迹精度的影响。实验表明，减小interval与提高速度均有助于提升插补精度，使轨迹更接近理想圆形。

最近简单的了解了一下圆弧插补的实现过程，其实现的简单代码如下，代码中有些缺陷，后面将会修改。
插补的相关参数如下，
半径10，圆弧中心(0,0),起始点(10,0)。

实验结果

`代码中单个插补周期中的每个轴运动间隔为interval,在实际的运动控制过程中
interval=t*v
式中,t为插补周期，v为运动的速度。
所以该间隔受t和v的综合影响。
当interval=0.5时，插补图形为
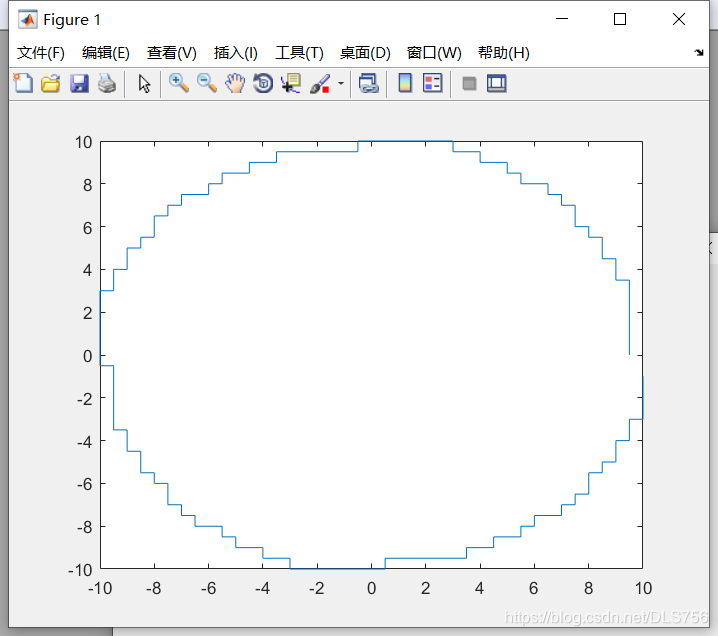
在这里插入图片描述
当interval=0.1时

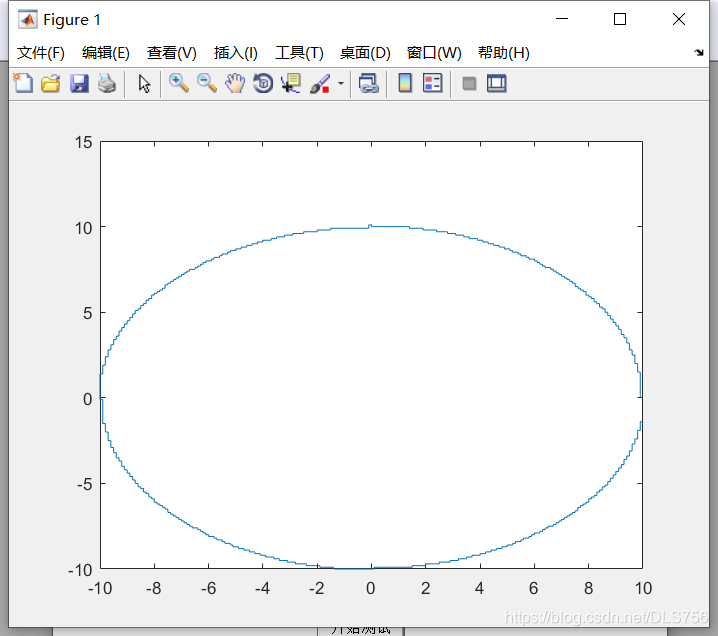
当interval=0.01时，插补图形如下：

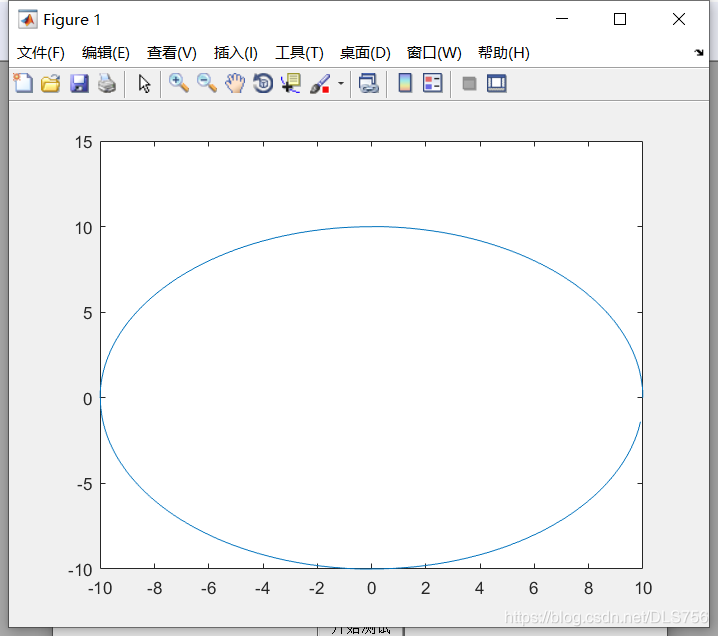
可见当interval减小时，插补的轨迹也比较密集，而且更接近于实际的圆。
所以减小插补走起与速度都有利于提升插补的精度。

代码如下。

 double x0=0,y0=0;  //圆心 
 double x=10,y=0;    //起始点
 double F,interval=0.01,F1;   //  
 int times=0;
 while(TRUE)
 {
  F=(x-x0)*(x-x0)+(y-y0)*(y-y0)-100;    //关键公式
  F1=(x-10)*(x-10)+(y-0)*(y-0);
     cout<<F<<" "<<F1<<"\n";
 if(x>=0&&y>=0)
 {   
  if(F>=0)
  {
   x=x-interval;
  }
        else
  {
   y=y+interval;
  }
  cout<<x<<" "<<y<<"\n";
  out<<x<<" "<<y<<"\n";
 }
 else if(x<=0&&y>=0)
 {
  if(F>=0)
  {
   y=y-interval;
  }
  else
  {
            x=x-interval;
  }
  cout<<x<<" "<<y<<"\n";
  out<<x<<" "<<y<<"\n";
 }
 else if(x<=0&&y<=0)
 {
  if(F>=0)
  {
           x=x+interval;
  }
  else
  {
   y=y-interval;
  }
  cout<<x<<" "<<y<<"\n";
  out<<x<<" "<<y<<"\n";
 }
 else if(x>=0&&y<=0)
 {
  if(F>=0)
  {
   y=y+interval;
  }
  else
  {
   x=x+interval;
  }
  cout<<x<<" "<<y<<"\n";
  out<<x<<" "<<y<<"\n";
 }
 if(times>0)
 {
  if(F1>1&&F1<2&&x>0&&y<0)
  {
   break;
  }
 }
 times++;
 }