ML, ZF, MMSE。MRC。。。。

有用的矩阵知识：在无线通信中，当信道矩阵 $\mathbf{H}$ 不是方阵或是奇异的，利用伪逆进行ZF预编码或ZF检测是非常有意义的，因为这可以最小化由于不完美的信道逆引起的干扰。

信道矩阵的伪逆，通常被称为Moore-Penrose伪逆，是一个广泛应用的数学工具，用于处理可能不是方阵或可能是奇异（不可逆）矩阵的矩阵。对于任意矩阵 $\mathbf{A}$，其伪逆记作 ${\mathbf{A}}^{†}$。

伪逆 ${\mathbf{A}}^{†}$ 的定义满足以下四个条件：

1. $\mathbf{A}{\mathbf{A}}^{†}\mathbf{A}=\mathbf{A}$
2. ${\mathbf{A}}^{†}\mathbf{A}{\mathbf{A}}^{†}={\mathbf{A}}^{†}$
3. $(\mathbf{A}{\mathbf{A}}^{†}{)}^{\ast }=\mathbf{A}{\mathbf{A}}^{†}$ （此处的 * 表示复共轭转置，对于实矩阵则为转置）
4. $({\mathbf{A}}^{†}\mathbf{A}{)}^{\ast }={\mathbf{A}}^{†}\mathbf{A}$

如果 $\mathbf{A}$ 是一个可逆的方阵，那么其伪逆就是其逆，即 ${\mathbf{A}}^{†}={\mathbf{A}}^{-1}$。但是，对于非方矩阵或奇异矩阵，伪逆提供了一种求逆的通用方法。

计算矩阵的伪逆的一种常用方法是使用奇异值分解 (SVD)。给定矩阵 $\mathbf{A}$ 的奇异值分解为：
$$\mathbf{A}=\mathbf{U\Sigma }{\mathbf{V}}^{\ast }$$
其中，$\mathbf{U}$ 和 $\mathbf{V}$ 分别是左奇异向量和右奇异向量矩阵，而 $\mathbf{\Sigma }$ 是一个对角矩阵，其对角线上的元素是 $\mathbf{A}$ 的奇异值。

伪逆 ${\mathbf{A}}^{†}$ 可以表示为：
$${\mathbf{A}}^{†}=\mathbf{V}{\mathbf{\Sigma }}^{†}{\mathbf{U}}^{\ast }$$
其中，${\mathbf{\Sigma }}^{†}$ 是 $\mathbf{\Sigma }$ 的伪逆，其是通过取 $\mathbf{\Sigma }$ 的非零元素的倒数然后再进行转置得到的。

图1：发射端可以获得CSI时的模态分解

# MIMO技术：空间复用

1. 均衡（Equalization）:

   • 目的：均衡是在接收端用于补偿无线信道造成的多径衰减和干扰的技术。
   • 工作原理：通过对接收到的信号进行滤波或处理，均衡器试图还原发送端的原始信号。
   • 类型：常见的均衡器包括零干扰（ZF）、最小均方误差（MMSE）均衡器等。

2. 预均衡（Pre-Equalization）:

   • 目的：与传统均衡不同，预均衡是在发送端进行的，目的是预先补偿信道的影响，从而简化接收端的处理。
   • 工作原理：要进行预均衡，发送端需要知道信道的信息。这通常通过信道状态信息反馈（CSI反馈）获得。

3. 预编码（Precoding）:

   • 定义：预编码是在发送端之前处理数据的技术，以优化多天线传输的性能。预编码考虑了接收天线如何看待信道，并根据这些信息优化发送信号。
   • 目的：通过预先调整发送信号，预编码旨在降低或消除信道中的干扰和衰减，从而提高数据传输的性能。
   • 工作原理：为了实现预编码，发送端通常需要知道信道的状态信息（CSI）。有了这些信息，发送端可以调整每个天线发送的信号，使其在接收端叠加以最佳方式。

4. 波束成形（Beamforming）:

   • 定义：波束成形是使用多个天线来集中或定向无线能量，以增强一个特定方向上的信号传输。
   • 目的：通过聚焦无线能量，波束成形可以增强特定方向上的信号质量，从而提高信号到噪声比（SNR）。
   • 工作原理：在MIMO系统中，波束成形通过调整每个天线的相位和振幅来实现。这确保了所有的天线在期望的方向上产生的信号相互增强，而在其他方向上则相互抵消。。

波束成形（Beamforming）和预编码（Precoding） 都是多输入多输出（MIMO）无线通信系统中的关键技术。它们都涉及到如何优化发送信号，以最大化接收信号的质量或满足其他某种性能指标。尽管这两个术语有时互换使用，但它们的目的和应用有所不同。

区别: 虽然两者都涉及优化发送信号，但波束成形主要关注于如何集中无线能量，以增强特定方向上的信号传输；而预编码更关注于如何根据接收端和信道的特性来优化每个天线的发送信号。

相似点: 在实际应用中，波束成形和预编码往往结合使用，以获得最佳的通信性能。例如，一个系统可能首先使用波束成形技术来集中无线能量，然后使用预编码技术来进一步优化发送信号。

5. 信号检测
   信号检测是通信系统中的一个关键过程，涉及确定一个特定的信号或消息是否存在于接收到的数据中。在数字通信中，信号检测主要是关于如何最佳地估算或检测发送的符号。信号检测可以分为两大类：确定性检测和统计检测。

确定性检测：这是当我们有确切知道的信号模型并试图在噪声中检测它时使用的方法。
统计检测：当我们对信号或噪声只有统计信息时使用的方法。

在数字通信中，常用的信号检测方法有：

• 匹配滤波器检测：该方法涉及使用一个与预期信号匹配的滤波器来最大化信号到噪声比 (SNR)。输出然后与一个阈值进行比较来做出决策。
• 最大似然 (ML) 检测：这种方法是基于最大化接收信号的似然函数来做出决策。
• 最近邻居或最小距离检测：在这种方法中，接收符号与所有可能的发送符号进行比较，并选择距离最近的符号作为估计。
• ZF检测: 主要目标是消除或“迫使”信道引起的干扰为零，在多用户MIMO系统中，它可以帮助消除不同用户之间的干扰。
• 均方误差 (MSE) 或 MMSE 检测：这种方法尝试最小化估计符号与实际符号之间的均方误差，它试图在消除干扰和最小化噪声放大之间找到一个平衡。

ZF技术

ZF（Zero-Forcing）技术的主要目标是消除多用户干扰或多路径干扰。在MIMO（多输入多输出）系统中，ZF技术特别用于预编码或均衡，以实现此目的。

假设信道矩阵为 $\mathbf{H}$，其中包含来自每个发射天线到每个接收天线的信道系数。在多用户MIMO场景中，该矩阵描述了从每个发射机到每个接收机的所有路径。

1. ZF均衡:
   接收端可以使用ZF均衡来消除多路径干扰。接收到的信号 $\mathbf{y}$ 为:
   $$\mathbf{y}=\mathbf{Hx}+\mathbf{z}$$
   其中，$\mathbf{z}$ 是噪声。

   ZF均衡的输出为:
   $${\hat{\mathbf{s}}}_{ZF}={\mathbf{G}}_{ZF}\mathbf{y}$$
   其中，${\mathbf{G}}_{ZF}$ 是ZF均衡矩阵。

   为了消除干扰，ZF均衡矩阵 ${\mathbf{G}}_{ZF}$ 可以选择为:
   $${\mathbf{G}}_{ZF}={\mathbf{H}}^{†}$$
   这样，通过乘以ZF加权矩阵（无论是在发送端还是接收端），都可以有效地消除多路径或多用户干扰。然而，ZF方法的一个主要缺点是，在低信噪比（SNR）条件下，它可能会放大噪声，因为它不考虑噪声的存在。

2. ZF信号检测
   ZF信号检测的加权矩阵与ZF均衡的加权矩阵相同，但在两种情境中的应用是有所不同的。信号均衡强调的是在传输过程中如何消除或减少由信道引入的失真。而信号检测更侧重于在接收端正确地估计发送的符号。

   使用SVD，检测后的噪声功率（与差错性能相关）的期望值为
   $$\begin{array}{rl}E\left\{{\Vert {\tilde{\mathbf{z}}}_{\text{ZF }}\Vert }_2^2\right\}& =\mathbf{E}\left\{{\Vert {\Sigma }^{-1}{\mathbf{U}}^{\mathrm{H}}\mathbf{z}\Vert }_2^2\right\}\\ & =\sum _{i=1}^{N_{\text{Tx }}}\frac{{\sigma }_z^2}{{\sigma }_i^2}\end{array}$$

3. ZF预均衡
   ZF 预均衡的目标是消除或最小化多用户干扰。但在实际应用中，特别是在MIMO系统中，我们通常还需要考虑发送功率的约束。为满足预均衡后总发射功率不变，我们需要ZF均衡矩阵${\mathbf{G}}_{ZF}$进行归一化。具体地，我们可以使用以下方式归一化：
   $${\mathbf{G}}_{ZF,normalized}=\frac{{\mathbf{G}}_{ZF}}{\sqrt{\text{tr}({\mathbf{G}}_{ZF}{\mathbf{G}}_{ZF}^H)}}$$
   这里，$\text{tr}(\cdot )$ 表示矩阵的迹（即矩阵对角线元素的和），并且 ${\mathbf{G}}_{ZF}^H$ 是矩阵 ${\mathbf{G}}_{ZF}$ 的厄尔米特转置（共轭转置）。

   这样，归一化的ZF预均衡矩阵 ${\mathbf{G}}_{ZF,normalized}$ 会确保整体发射功率与没有预均衡时相同，从而满足常见的发射功率限制。

4. ZF预编码:
   为了消除发射端的多用户干扰，可以使用ZF预编码技术。预编码器将信号加权，以便当它们经过信道时，多用户干扰在接收端被消除。

   发送向量 $\mathbf{x}$ 可以表示为:
   $$\mathbf{x}={\mathbf{W}}_{ZF}\mathbf{s}$$
   其中，$\mathbf{s}$ 是待发送的符号向量，${\mathbf{W}}_{ZF}$ 是ZF预编码矩阵。

   为了确保在接收端接收到的信号没有干扰，ZF预编码矩阵可以定义为信道矩阵的伪逆，即:
   $${\mathbf{W}}_{ZF}={\mathbf{H}}^{†}=({\mathbf{H}}^H\mathbf{H}{)}^{-1}{\mathbf{H}}^H(假设({\mathbf{H}}^H\mathbf{H})是可逆的)$$
   其中，${\mathbf{H}}^{†}$ 是信道矩阵 $\mathbf{H}$ 的伪逆。

总结：ZF技术的核心是使用信道矩阵的逆来消除信道造成的干扰，无论是在接收端还是发射端，权重矩阵的表达式都是一样的。
使用ZF技术的均衡、信号检测、预均衡、预编码的权重矩阵表达式一样，但是均衡和信号检测发生在接收端，预均衡和预编码发生在发射端。

MMSE技术

MMSE（最小均方误差）技术是另一种常用于MIMO系统的线性处理方法，能够最大化检测后的SINR。与ZF方法相比，MMSE方法在低信噪比（SNR）环境中具有更好的性能，因为它考虑到了噪声的影响。

1. MMSE均衡:
   MMSE均衡器的权重矩阵为：
   $${\mathbf{G}}_{MMSE}=({\mathbf{H}}^H\mathbf{H}+{\sigma }_z^2\mathbf{I}{)}^{-1}{\mathbf{H}}^H$$
   其中 $\mathbf{I}$ 是单位矩阵， ${\mathbf{H}}^H$ 是信道矩阵的Hermitian转置（共轭转置）。

2. MMSE信号检测
   MMSE信号检测的加权矩阵与MMSE均衡的加权矩阵相同，但在两种情境中的应用是有所不同的。信号均衡强调的是在传输过程中如何消除或减少由信道引入的失真。而信号检测更侧重于在接收端正确地估计发送的符号。
   使用SVD，检测后的噪声功率（与差错性能相关）的期望值为
   $$\begin{array}{rl}E\left\{{\Vert {\tilde{z}}_{\text{MMSE }}\Vert }_2^2\right\}& =E\left\{{\left(\Sigma +{\sigma }_z^2{\Sigma }^{-1}\right)}^{-1}{\mathbf{U}}^{\mathrm{H}}z{\Vert }^2\right\}\\ & =\sum _{i=1}^{N_{\mathrm{Tx}}}\frac{{\sigma }_z^2{\sigma }_i^2}{{\left({\sigma }_i^2+{\sigma }_z^2\right)}^2}\end{array}$$

3. MMSE预均衡:
   MMSE预均衡基本上是在发射端应用MMSE预编码。其目标是在发送信号前对其进行加权，从而最小化接收端的误差。这样，在接收端可能就不需要进一步的均衡处理。
   注意：在实际应用中，为了满足功率约束，MMSE预编码和预均衡矩阵可能需要进行归一化。

4. MMSE预编码:
   给定信道矩阵 $\mathbf{H}$ 和噪声方差 ${\sigma }^2$，应用于发射端的MMSE预编码的权重矩阵可以表示为：
   $${\mathbf{W}}_{MMSE}={\mathbf{H}}^H(\mathbf{H}{\mathbf{H}}^H+\frac{{\sigma }_z^2}{{\sigma }_x^2}\mathbf{I}{)}^{-1}$$

在发射端使用预均衡的效果避灾接收端使用均衡的效果更好，因为接收机在均衡过程中会受到噪声增强的影响。

比较ZF检测和MMSE检测，引入ML检测

当信道矩阵的条件数很大, 即最小的奇异值非常小时, 在线性波波的过程中噪声增强的影响将会更加显著。 对于 ZF 和 MMSE 线性检测器, 由最小奇异值引起噪声增强的影响分别为
$$E\left\{{\Vert {\tilde{z}}_{\mathrm{ZF}}\Vert }_2^2\right\}=\sum _{i=1}^{N_{\max }}\frac{{\sigma }_z^2}{{\sigma }_i^2}\approx \frac{{\sigma }_z^2}{{\sigma }_{\min }^2},\mathrm{ZF}$$

$$E\left\{{\Vert {\tilde{z}}_{\text{MMSE }}\Vert }_z^2\right\}=\sum _{j=1}^{N_{\mathrm{TH}}}\frac{{\sigma }_z^2{\sigma }_i^2}{{\left({\sigma }_i^2+{\sigma }_z^2\right)}^2}\approx \frac{{\sigma }_z^2{\sigma }_{\min }^2}{{\left({\sigma }_{\min }^2+{\sigma }_z^2\right)}^2}\text{, MMSE }$$

其中, ${\sigma }_{\min }^2=\min \left\{{\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_{N_{\mathrm{Tx}}}^2\right\}$，${\sigma }_z^2$表示接收天线佳兴高斯白噪声方差。比较上面两个式子, 很明显噪声增强的影响在 $\mathrm{ZF}$滤波中比在 MMSE 滤波中更加显著。如果 ${\sigma }_{\min }^2\gg {\sigma }_z^2$, 那么 ${\sigma }_{\min }^2+{\sigma }_z^2\approx {\sigma }_{\min }^2$, 所以在两种线性滤波中噪声增强的影响是相同的。由于 $\mathrm{ZF}$ 技术实现的分集阶数为 $N_{\mathrm{Rx}}-N_{\mathrm{Tx}}+1$, 在单发射天线和多接收天线的情况下, $\mathrm{ZF}$ 接收机相当于一个最大比合并 ( $\mathrm{MRC}$ ) 接收机, 可以实现的分集阶数为 $N_{\mathrm{Rx}}$ 。

在多径衰落信道中, 最大似然序列检测器 (MLSD) 是最优的检测器。根据在连续符号间隔内接收到的符号序列的观察值, MLSD 以最大化后验概率做出判决。它的复杂度取决于调制阶数和多径数。令 $M$ 表示每个调制符号可能的信号点个数, $L$ 表示在多径衰落信道上产生的 ISI 跨度。因为 ISI 跨度的记忆长度为 $L$, 所以 $M^L$ 为相应的欧氏距离的度量, 用于在 MLSD 中选择最佳的序列。通过增大 $M$, 可以找到更有效的传输, 实现更高的数据速率, 但是最优均衡器的复杂度将变得不可接受。例如, 在时延扩展为 $10\mu \mathrm{s}$ 的多径衰落信道上, 传输采用 $64-\mathrm{QAM}$ 的 $10\mathrm{Mbps}$ 数据,对于 $L\approx 16,M^L=64^{16}$ 。当 $M$ 和 $L$ 太大时, 可以使用次优但更加实用的均衡器, 如最小均方误差 (Minimum Mean Square Error, MMSE) 和最小二乘 (Least Square, LS) 均衡器。

ML (最大似然) 信号检测是一种非线性检测技术，旨在最小化误码率 (BER)。在高SNR (信噪比) 条件下，ML检测为MIMO系统提供最佳性能，但计算复杂度也很高。

考虑一个 $N\times M$ 的MIMO系统，其中 $N$ 是接收天线的数量，而 $M$ 是发送天线的数量。给定信道矩阵 $\mathbf{H}$，接收到的信号向量 $\mathbf{y}$ 可以表示为：

$$\mathbf{y}=\mathbf{Hs}+\mathbf{n}$$

为了估计发送的符号 $\mathbf{s}$，我们可以使用ML检测。ML检测的目标是找到一个符号向量 ${\mathbf{s}}_{est}$，使得以下欧几里得距离最小：

$$\hat{\mathbf{s}}=\arg \underset{{\mathbf{s}}_{est}}{\min }{\Vert \mathbf{y}-\mathbf{H}{\mathbf{s}}_{est}\Vert }^2$$

这基本上是在所有可能的发送符号向量中找到一个，该向量与实际接收到的信号 $\mathbf{y}$之间的距离最小。所以ML检测的计算复杂度很高，对于每一个可能的发送符号组合，都需要计算距离，因此计算量与可能的符号组合数量成指数增长。所以在实际应用中，常常使用一些子最优算法（如球形检测、逐层搜索等）来近似ML检测，以平衡性能与计算复杂度。

---------------------------------这是分割线-------------------------
分集技术主要关注提高信号质量和可靠性，而空间复用技术主要关注增加系统容量和吞吐量。

空间复用技术 (Spatial Multiplexing Techniques)的实现模块：

1. 多天线阵列：空间复用，特别是在MIMO系统中，需要使用多个发送和接收天线。

2. 信道状态信息 (CSI) 估计：为了有效地进行空间复用，发送端和接收端都需要知道信道的状态。因此，需要有机制来估计和反馈CSI。

3. 空间复用编码器：在发送端，空间复用编码器会将信息数据流映射到多个天线。

4. 空间复用解码器：在接收端，解码器会根据CSI从接收到的信号中分离和恢复原始的数据流。

5. 波束赋形算法：在某些应用中，可以使用波束赋形技术来聚焦或指向信号，从而进一步提高空间复用的效益。这需要复杂的算法和权重计算。

6. SDMA控制器：对于空间分割多址接入 (SDMA)，需要一个控制器来管理用户之间的空间隔离和资源分配。

这些模块在实际的无线通信系统中可能会根据特定的应用和需求进行调整和优化。同时，为了提高系统的性能和可靠性，这些模块往往会与其他无线通信技术结合使用。

分集技术 (Diversity Techniques)的实现模块：

1. 多天线系统：分集通常使用多个接收和/或发送天线来实现。每个天线都会从稍微不同的路径接收信号，从而为分集提供独立或部分独立的信号复制。

2. 切换器或合并器：在接收端，根据采用的分集策略，可以使用切换器选择最佳的信号源，或者使用合并器将来自不同天线的信号合并。

3. 分频器：对于频率分集，可以使用分频器将输入信号分成不同的频率带宽。

4. 延迟元件：对于时间分集，延迟元件可用于创建信息符号的时间偏移。

5. 分集解码器：在接收端，一个解码器会根据采用的分集策略对多个信号副本进行处理，以恢复原始信息。

--------------------------这是分割线--------------------------------

MIMO技术：分集技术

分集技术是无线通信中用于提高通信可靠性和降低误码率的技术。它的主要思想是利用多个独立或部分独立的信号路径来传输或接收信息，主要目的是将不稳定的无线时变衰落信道转变成像AWGN信道一样没有显著瞬时衰落的稳定信道。分集技术可以有效地对抗多径衰减、暂态干扰等现象。以下是关于发射分集和接收分集的简介：

1. 发射分集 (Transmit Diversity):
   • 定义：发射分集是在发送端使用多个天线发射相同或不同的信号复制到接收端。通过这种方式，可以确保至少有一个信号路径得到良好的接收。
   • 优点：可以有效地对抗信道衰减和多径干扰，提高信号质量。
   • 实现：常见的方法包括空间发射分集、频率/时间发射分集等。

时间、频率和空间分集的示意图

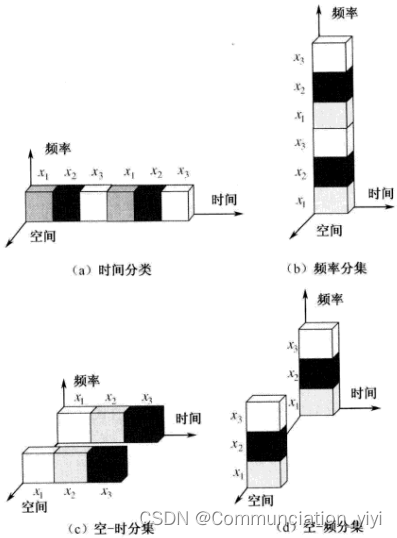
2. 接收分集 (Receive Diversity):
   • 定义：接收分集是在接收端使用多个天线来捕获从同一发送端发出的信号副本。每个天线捕获的信号可能会因为经过不同的传播路径而有所不同。
   • 优点：通过合并或选择多个天线上的信号，可以得到更好的信号质量和更低的误码率。
   • 实现：常见的方法包括最大比合并 (Maximum Ratio Combining, MRC)、选择合并 (Selection Combining, SC)等。

考虑一个具有 $N_{\mathrm{Rx}}$ 根接收天线的接收分集系统， 假设只有一根发射天线，$N_{\mathrm{Rx}}$ 个独立的瑞利衰落信道可以表示为
$$\mathbf{h}={\left[h_1{h}_2\cdots h_{N_{\mathrm{Rx}}}\right]}^{\mathrm{T}}$$

令 $x$ 表示具有单位方差 (功率) 的发射信号, 则接收信号 $\mathbf{y}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times 1}$ 可以表示为

$$\mathbf{y}=\sqrt{\frac{E_x}{N_0}}\mathbf{h}x+\mathbf{z}$$

其中, $\mathbf{z}$ 为 零均值循环对称复高斯ZMCSCG 噪声, 满足 $E\left\{\mathbf{z}{\mathbf{z}}^{\mathrm{H}}\right\}={\mathbf{I}}_{N_{\mathrm{Rx}}}$ 。可以通过多种技术合并不同天线上的接收信号,包括选择合并 (Selection Combining, SC)、最大比合并 (Maximal Ratio Combing, MRC) 和等增益合并 (Equal Gain Combining, EGC)。

• 在 SC 中, 从 $N_{\mathrm{Rx}}$ 个支路中选择 SNR 最大的接收信号进行解码。令 ${\gamma }_i$ 为第 $i$ 个支路的瞬时 SNR:
  $${\gamma }_i={\left|h_i\right|}^2\frac{E_x}{N_0},i=1,2,\cdots ,N_{\mathrm{Rx}}$$
  $\mathrm{SC}$ 的平均 SNR 由下式给出:
  $${\rho }_{\mathrm{sC}}=E\left\{\underset{i}{\max }\left({\left|h_i\right|}^2\right)\right\}\cdot \frac{E_x}{N_0},i=1,2,\cdots ,N_{\mathrm{Rx}}$$

• 在 MRC 中, 通过下面的加权求和方式对 $N_{\mathrm{Rx}}$ 个支路进行合并:
  $$y_{\mathrm{MRC}}=\underset{{\mathrm{w}}_{\mathrm{MRC}}^{\mathrm{T}}}{\underbrace{\left[w_1^{(\mathrm{MRC})}{w}_2^{(\mathrm{MRC})}\cdots w_{N_R}^{(\mathrm{MRC})}\right]}}\mathbf{y}=\sum _{i=1}^{N_{\mathrm{Rx}}}{w}_i^{(\mathrm{MRC})}{y}_i$$
  其中, $\mathbf{y}$ 为接收信号, ${\mathbf{w}}_{\mathrm{MRC}}$ 为加权向量。 $y_i=\sqrt{\frac{E_x}{N_0}}{h}_{i}x+z_i$, 因此接收信号可以被分解为信号部分和噪声部分:
  $$\begin{array}{rl}{y}_{\text{MRC }}& ={\mathbf{w}}_{\text{MRC }}^{\mathrm{T}}\left(\sqrt{\frac{E_x}{N_0}}\mathbf{h}x+\mathbf{z}\right)\\ & =\sqrt{\frac{E_x}{N_0}}{\mathbf{w}}_{\text{MRC }}^{\mathrm{T}}\mathbf{h}x+{\mathbf{w}}_{\text{MRC }}^{\mathrm{T}}\mathbf{z}\end{array}$$
  上式中, 信号部分和噪声部分的瞬时平均功率分别为
  $$\begin{array}{rl}{P}_{\mathrm{s}}& =E\left\{{\left|\sqrt{\frac{E_x}{N_0}}{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\mathbf{hx}\right|}^2\right\}\\ & =\frac{E_x}{N_0}E\left\{|{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\mathbf{h}x{|}^2\right\}\\ & =\frac{E_x}{N_0}{\left|{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\mathbf{h}\right|}^2\end{array}$$
  和
  $$P_{\mathrm{z}}=E\left\{{\left|{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\mathbf{z}\right|}^2\right\}={\Vert {\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\Vert }_2^2$$
  结合上面两个式子，可以得到 MRC 的平均 SNR 为
  $${\rho }_{\mathrm{MRC}}=\frac{P_{\mathrm{s}}}{P_z}=\frac{E_x}{N_0}\frac{{\left|{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\right|}^2}{{\Vert {\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\Vert }_2^2}$$

引入柯西-许瓦兹不等式:
$${\left|{\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\mathbf{h}\right|}^2⩽{\Vert {\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\Vert }_2^2\Vert \mathbf{h}{\Vert }_2^2$$
MRC 平均 SNR的上限为
$${\rho }_{\text{MRC }}=\frac{E_x}{N_0}\frac{{\left|{\mathbf{w}}_{\text{MRC }}^{\mathrm{T}}\right|}^2}{{\Vert {\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\Vert }_2^2}⩽\frac{E_x}{N_0}\frac{{\Vert {\mathbf{w}}_{\text{MRC }}^{\mathrm{T}}\Vert }_2^2\Vert \mathbf{h}{\Vert }_2^2}{{\Vert {\mathbf{w}}_{\mathrm{MRC}}^{\mathrm{T}}\Vert }_2^2}=\frac{E_x}{N_0}\Vert {\mathbf{h}|}_2^2$$
当${\mathbf{w}}_{\mathrm{MRC}}={\mathbf{h}}^{\ast }$时MRC的SNR达到最大（不等式取等号），即在MRC中，各支路的加权系数必须与各自的信道匹配。EGC是MRC的一种特殊情况，各支路所有的信号以相同的加权值进行合并。

接收分集的缺点是接收端的计算负荷很高，可能导致下行链路中移动台的功耗很大，在发射端使用空时块码（Space-Time Coding, STC）同样可以获得分集增益，而在接收端解码时只需要简单的线性处理。为了进一步降低移动台的计算复杂度，可以采用不需要在接收端估计CSI的查分空-时码。关于空-时编码的内容将在下一节详细叙述。