Coding Practice，48天强训（5）

Topic 1：贪心

找出几个关键关系——you的数量是由abc中最小的数组决定的，先确定分数最高的you，然后将所有的oo连起来，这样就能得到最高分

所以max_s = min(a, b, c) * 2 + max(b - min(a, b, c) - 1, 0) * 1; 

b - min(a, b, c) - 1当b为b就是最小数时会变成负数，所以要和0 max一下，修正为0；

关于数组，还有输入和输出写的不熟练，一开始还在考虑用vector<vector<vector<int>>>来储存三个三个一组的数据

---

Topic 2：多源BFS 腐烂\洪水扩散问题

和昨天的DFS可以形成对比:

和leetcode 994 腐烂的橘子题目一样，通常的BFS问题都采用队列来解决，通过本位置的关联元素（没搜素过的）不断入队，然后本位置元素出队，来完成一轮一轮的辐射搜索

bfs还需要继续巩固，不熟练

---

Topic 3：约瑟夫环问题（龙年春晚 笑）

同leetcode 1823

我们多用几种方法来写一写，顺便复习复习数据结构，第一种方式，链表模拟，因为是环状结构，链表天然适合。

list的基本知识，注意注意更新end()哨兵位

第二种方法，通过数组来模拟环

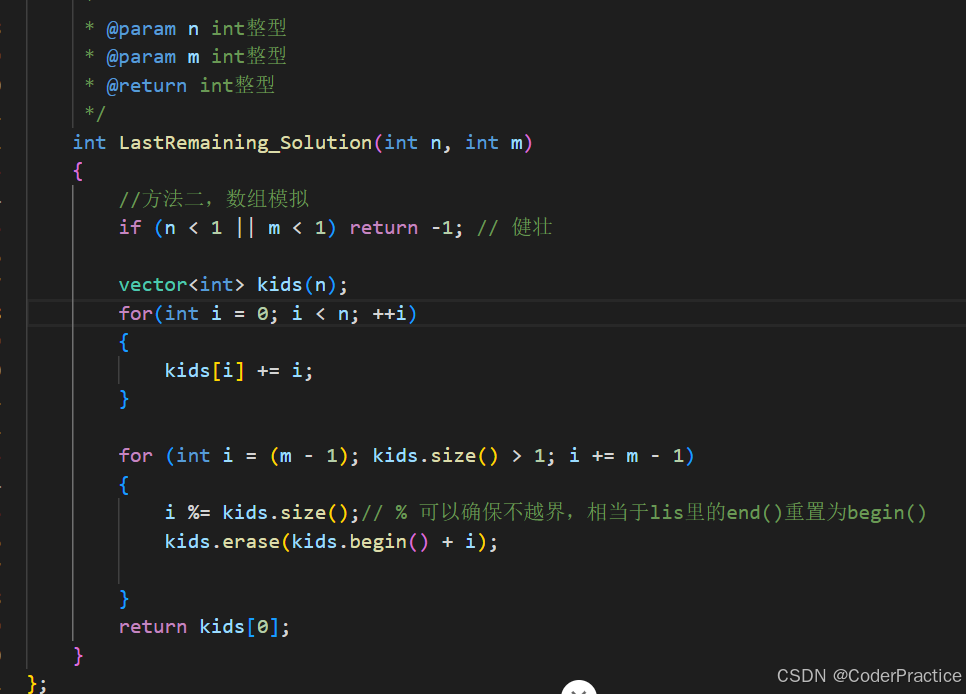
数组模拟也基本类似，关键点就是通过%运算来保证i += m-1不越界，当然数组也可以不用erase，用一个bool数组来标识删除条件也能解决，而且不用erase，不需要挪动数据应该会更快。

方法三：动态规划，也可说是递推/递归，找规律嘛

首先我们来画个图模拟一下，从下标0开始，在n个目标中找最后的幸存者，那么第一次遍历（紫色圈）就是从0到n-1；

然后我们根据条件，把m-1位置的人剔除，那么在第二次遍历时，第一圈的m，就变成了第二圈的0

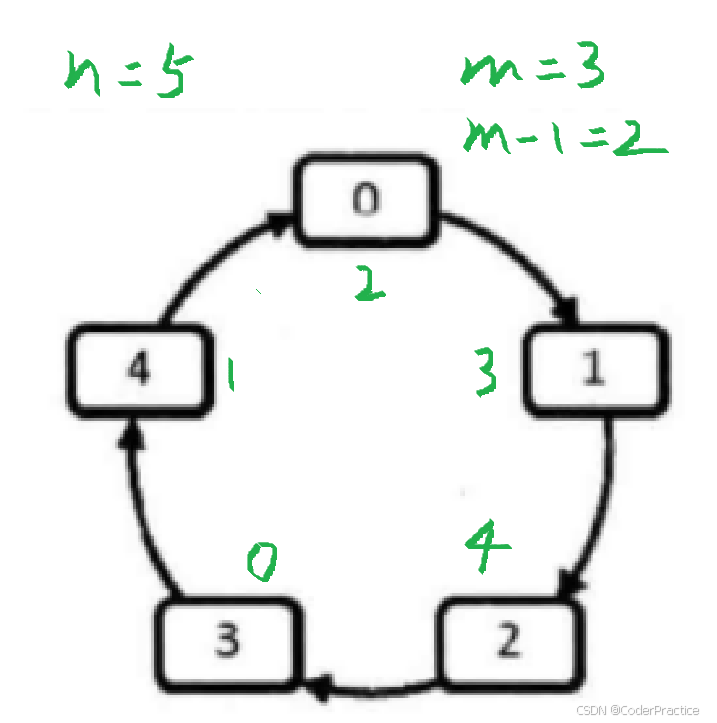如果还是不明白可以参考实际的情况来计算，比如左图

实际上就是相当于顺时针转了一下

好，那么我们搞清楚这个关系是为了啥呢？

一般我们做推导也好，做递归也罢，是不是都是把一个大问题切分成子问题，搞定子问题得基础上去重复操作？所以如果我们要求出：dp[i]——当有i个人时，幸存者得下标

我们就得知道dp[i]和dp[i-1]之间的关系，根据这个关系反推dp[i-2]  dp[i-3]  dp[i-4] ....dp[2]   dp[1]，而像dp[2]  dp[1] 这种我们是能直接算出来的，所以根据算的结果加个循环反推回去就获得dp[i]了

这就是所有动态规划、递推、递归的核心原理

那么现在我们知道了，这里我还是用n哈，数学公式上喜欢用dp[i]表示，我们之前拿n举的例子，这里就还是保持，我们说外圈的行为结果是dp[n], 内圈的结果是dp[n-1],根据上面的图分析，内圈的下标等于外圈的下标-m,外圈的下标等于内圈的下标+m

是不是

有些人会觉得n-m那里有问题，注意，这个n-m是指第二层这个位置的数字，不是说n-m=0，不要搞错了

好那么得到公式，这里把n改成i——dp[i]-m = dp[i - 1]    =   dp[i] = dp[i - 1] + m  

好好好，找到关系了，快接近正确答案了，那么dp[i - 1] = dp[i - 2] + m 再推一推  dp[i - 2] = dp[i - 3] + m，到这里有点不对劲了，我们把推的公式带回dp[i]里，那么

dp[i] = dp[i - 3] + m + m + m, 啊？怎么有这么多m，那肯定不对啊，越界越到姥姥家了，所以和上面数组的方式类似，我们需要对结果取个mod，确保永远在n的范围内，所以

dp[i] = (dp[i - 1] + m) % i  （这个i就是n） 现在完整的公式就出来了，那么那么已知，dp[1] = 0; 只有一个人的时候他自己就是胜利者嘛，就是下标0；

那么代码 

这样就搞定了，这几天发现后续的博客写作还是有很多要优化的地方，之后会考虑用优快云的代码编辑器模式来传代码，方便之后复习时ctrl F 搜索关键字，然后最近收到消息说部分同学的算法进度有点拖，所以把（6）更新完之后，算法笔试应该会先延迟一周，这一周大家补补视频再接着做。