Coding Practice，48天强训（24）

Topic 1：判断是不是平衡二叉树（递归）

判断是不是平衡二叉树_牛客题霸_牛客网

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 * };
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param pRoot TreeNode类 
 * @return bool布尔型
 */

int checkHeight(struct TreeNode* node) 
{
    if (node == NULL) return 0;
    int leftHeight = checkHeight(node->left);
    if (leftHeight == -1) return -1;
    int rightHeight = checkHeight(node->right);
    if (rightHeight == -1) return -1;
    if (abs(leftHeight - rightHeight) > 1) return -1;
    return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}

bool IsBalanced_Solution(struct TreeNode* pRoot ) 
{
    return checkHeight(pRoot) != -1;
}

平衡的递归过程

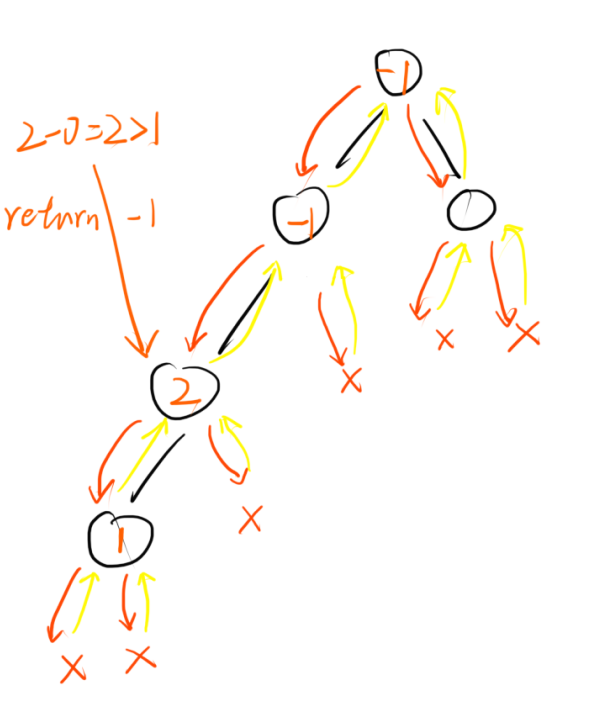不平衡的递归过程

---

Topic 2：最大子矩阵

最大子矩阵__牛客网

这题稍稍有点难度，leetcode中可以通过题目搜到，题目稍稍有些变动，方法很多，可以化繁为简通过转换为一维最大子序列和的方式来解，也可以数形结合来解

这里采用数形结合的方式

首先要确定的是在一个矩阵中，我们要确定一个矩阵的面积必须要有两个对角的点，左上右下or左下右上，总计4个坐标，所以可以通过四层for循环来找到对应的坐标

然后我们需要枚举出对应矩阵中所有元素的和，但是不能暴力，否则复杂度会上升到n^6，所以要采用二位前缀和的策略

创建一个dp数组，每个dp位来储存当前面积的元素总和，比如图中三角的位置储存了一个x，代表由左上到三角位置所有元素的和

dp中任意元素位置的值都是由它的上、左和左上三个位置的值决定的，由上图可以得知，其实是个面积的计算过程、绿色+蓝色-红色的面积，就是我们要计算的点（黄色）之前所有的面积，把其中的元素的和都相加，最后再加上黄色部分的值，就得出我们需要计算的面积中所有的值——dp[i][j]

ok，得出了dp表后我们就循环去填dp表的值，那么现在所有的已起始左上角和自选右下角的点所有的数值都已经确定，我们只要不断控制左上角的点遍历，来计算max值即可，如下图

我要计算x1,y1到x2,y2之间矩形面积的所有值的和

也是相同的思路，矩形的面积，用最大的绿色-红色-蓝色，此时多减了一个黄色，再加回来，最后就得到右下这块绿色阴影部分的面积了，再把该面积的所有值相加，就得到的答案

#include <iostream>
#include <climits>
using namespace std;

const int N = 110;// 数据量100,每行列多10用来放0下标的数据
// 遍历时从1开始，避免数组越界

int n;
int dp[N][N];

int main() 
{
    cin >> n;
    int x;
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            cin >> x;
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + x;
        }
    }

    int ret = INT_MIN;// .h  climits
    for(int x1 = 1; x1 <= n; ++x1)
    {
        for(int y1 = 1; y1 <= n; ++y1)
        {
            for(int x2 = x1; x2 <= n; ++x2)
            {
                for(int y2 = y1; y2 <= n; ++y2)
                {
                    ret = max(ret, dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]);
                }
            }
        }
    }
    cout << ret << endl;
}

---

Topic 3：小葱的01串(滑动窗口)

小葱的01串

注意这是一个环形结构，首尾也可以视作一对

可以视作这样的对应关系

所以我们只需要调整两个指针形成的红色区间，保持几个条件：

区间元素数量=总数 / 2

区间内的对应01的数量和区间外相等

#include<bits/stdc++.h>
using namespace std;

int main() {
    int n;          // 字符串长度
    string s;       // 01字符串
    cin >> n >> s;  // 读取输入

    int total0 = 0;// 统计字符串中'0'的总数,根据题意，总数为偶，并且只有01，所以只用考虑一个数，因为剩下的1肯定是总数-0
    for(const char& c : s) total0 += (c == '0');// 如果是'0'就加1，统计出全部的0的数量

    if(total0 % 2) { cout << 0; return 0; }// 如果'0'的总数是奇数，直接输出0（无法平分）

    int target = total0 / 2;// 目标：红色区域需要包含的'0'的数量，是0的总数/2
    int cnt = 0;// 当前窗口中的'0'的计数
    int res = 0;// 结果

    for(int i = 0; i < n/2; i++) cnt += (s[i] == '0');// 初始化：计算第一个窗口[0, n/2-1]中的'0'的数量
    
    if(cnt == target) res++;// 如果第一个窗口满足条件，结果加1

   
    for(int i = 1; i < n; i++)// 从下标1开始，滑动窗口每次移动一位，检查新窗口
    {
        cnt -= (s[i-1] == '0'); // 移除离开窗口的字符（左边界）
        cnt += (s[(i + n/2 - 1) % n] == '0');// 添加进入窗口的字符（右边界），使用模运算处理环形
        //(i + n/2 - 1) % n 是处理环形结构的关键，在环形字符串中，第n-1个字符的下一个字符是第0个字符
        //a % b 的结果是a除以b的余数，这正好可以实现"循环"效果，相当于转弯圈之后又从头转 
        //n：字符串总长度 
        //n/2：滑动窗口的长度（因为题目要求区间长度是n/2）
        //i：当前窗口的起始位置
        //计算窗口的右边界：窗口范围是 [i, i + n/2 - 1]，所以右边界位置是 i + n/2 - 1
        //为什么要模n：当 i + n/2 - 1 ≥ n 时，说明窗口右边界超出了字符串末尾，
        //这时：(i + n/2 - 1) % n 会得到这个位置在环形结构中的实际位置,相当于从字符串开头重新计算位置
        
        if(cnt == target) res++;// 如果满足条件，结果加1
    }

    cout << res;  // 输出最终结果
    return 0;
}

能听懂再写，不代表能自己独立解决，要反复复习，要吃透