Coding Practice，48天强训（33）

最新推荐文章于 2025-12-01 22:20:41 发布

原创最新推荐文章于 2025-12-01 22:20:41 发布 · 481 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #dfs

Topic 1：跳台阶扩展问题

跳台阶扩展问题_牛客题霸_牛客网

和经典的跳台阶问题不同的是，这只青蛙劲比较大，一次能跳n个台阶，用dp也能解决，两层for循环，就是效率可能会差一些

我们可以定义 dp[i] 表示跳上第 i 级台阶的跳法总数。根据题意，青蛙可以一次跳 1 到 i 级台阶，因此 dp[i] 可以表示为前面所有 dp[0] 到 dp[i-1] 的和，即：

dp[i] = dp[i−1] + dp[i−2] + …... + dp[0]

初始条件是 dp[0] = 1（表示在地面有一种方法），这里可能有疑惑，为啥没跳站在地面上也算1？因为如果 dp[0] = 0，那么当i = 1时，dp[1] = 0，这与实际情况矛盾（跳上第1级台阶应该有1种方法：直接跳1级），所以dp[0] = 1 表示“青蛙在地面时有一种方法”，即“不需要跳”也是一种“方法”，这样才符合实际情况也符合递推公式，那么代码是这样的

class Solution {
public:
    int jumpFloorII(int number) 
    {
        if (number == 0) return 1;
        vector<int> dp(number + 1, 0);
        dp[0] = 1; // 初始条件
        dp[1] = 1; // 跳上第1级台阶只有一种方法

        for (int i = 2; i <= number; ++i) //i从2到n
        {
            //dp[i] 是前面所有 dp[j]（j 从 0 到 i-1）的和
            for (int j = 0; j < i; ++j) dp[i] += dp[j];
        }
        return dp[number];
    }
};

优化一下，

dp[0] = 1

dp[1] = dp[0] = 1

dp[2] = dp[0] + dp[1] = 2

dp[3] = dp[0] + dp[1] + dp[2] = 4

dp[4] = dp[0] + dp[1] + dp[2] + dp[3] = 8

可以看出 dp[i] = 2 * dp[i-1]，因此可以只维护一个变量来存储前一个状态

class Solution {
public:
    int jumpFloorII(int number) 
    {
        if (number == 0) return 1;
        int prev = 1; //dp[1] = 1;

        for (int i = 2; i <= number; ++i) prev *= 2;
        
        return prev;
    }
};

那么我们可以看到，方法数其实就是2的指数幂，最后要得到的n就等于2^(n-1)，所以最终版本，我们可以用位运算的左移来进行快速幂计算

0001 << 就相当于乘方，最终是这样

class Solution {
public:
    int jumpFloorII(int number) {
        return 1 << (number - 1);  // 等同于 pow(2, number - 1)
    }
};

这里虽然题目说了number>=1,但是日常写为了健壮性还是补一个if (number == 0) return 1;靠谱；

Topic 2：包含不超过两种字符的最长子串(滑动窗口)

包含不超过两种字符的最长子串_牛客题霸_牛客网

#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;

int main() {
    string s;
    cin >> s;
    
    unordered_map<char, int> count;
    int left = 0, maxLen = 0;
    
    for (int right = 0; right < s.size(); ++right) {
        count[s[right]]++;
        
        // 如果窗口中字符种类超过2，收缩左边界
        while (count.size() > 2) {
            count[s[left]]--;
            if (count[s[left]] == 0) {
                count.erase(s[left]);
            }
            left++;
        }
        
        maxLen = max(maxLen, right - left + 1);
    }
    
    cout << maxLen << endl;
    return 0;
}

通常会用unordered_map<char, int>来写，但是可以有一些小优化

#include <bits/stdc++.h>
using namespace std;

int main() 
{
    //滑动窗口来接解决
    string s; cin >> s;
    //这里通常采用经典解法，会使用一个 unordered_map<char, int>
    //用来记录子数字的字符与数量情况，但是根据本题的字符数
    //我们可以采用一个vector<int>(26)来映射处理，优化开销
    vector<int> count (26, 0);// 储存26个字母
    int l = 0, r = 0, type = 0, res = 0;//左右指针、字符类型统计、结果
    for(;r < s.size(); ++r)
    {
        if(count[s[r] - 'a']++ == 0) type++;//如果之前count没有这个字符，增加type
        //顺便把count[s[r]]++ 记录当前字符
        while(type > 2)
        {
            if(--count[s[l] - 'a'] == 0) type--;
            //--count[s[l] - 'a'],直到等于0，把这个字符类型剔除，维持type只有两种
            l++;// 移动左标维持合法窗口
        }
        res = max(res, r - l + 1);
    }
    cout << res << endl;
}

这种写法把++ -- 判断藏在了if条件里，看起来很炫，其实易读性更差，拆出来写也很好，重剑无锋，大巧不功，质朴才是最高境界

#include <bits/stdc++.h>
using namespace std;

int main() 
{
    string s; cin >> s;
    vector<int> count (26, 0);
    int l = 0, r = 0, type = 0, res = 0;
    for(;r < s.size(); ++r)
    {
        if(count[s[r] - 'a'] == 0) type++;
        count[s[r] - 'a']++;
        while(type > 2)
        {
            count[s[l] - 'a']--;
            if(count[s[l] - 'a'] == 0) type--;
            l++;
        }
        res = max(res, r - l + 1);
    }
    cout << res << endl;
}

Topic 3：字符串的排列(DFS/递归)

字符串的排列_牛客题霸_牛客网

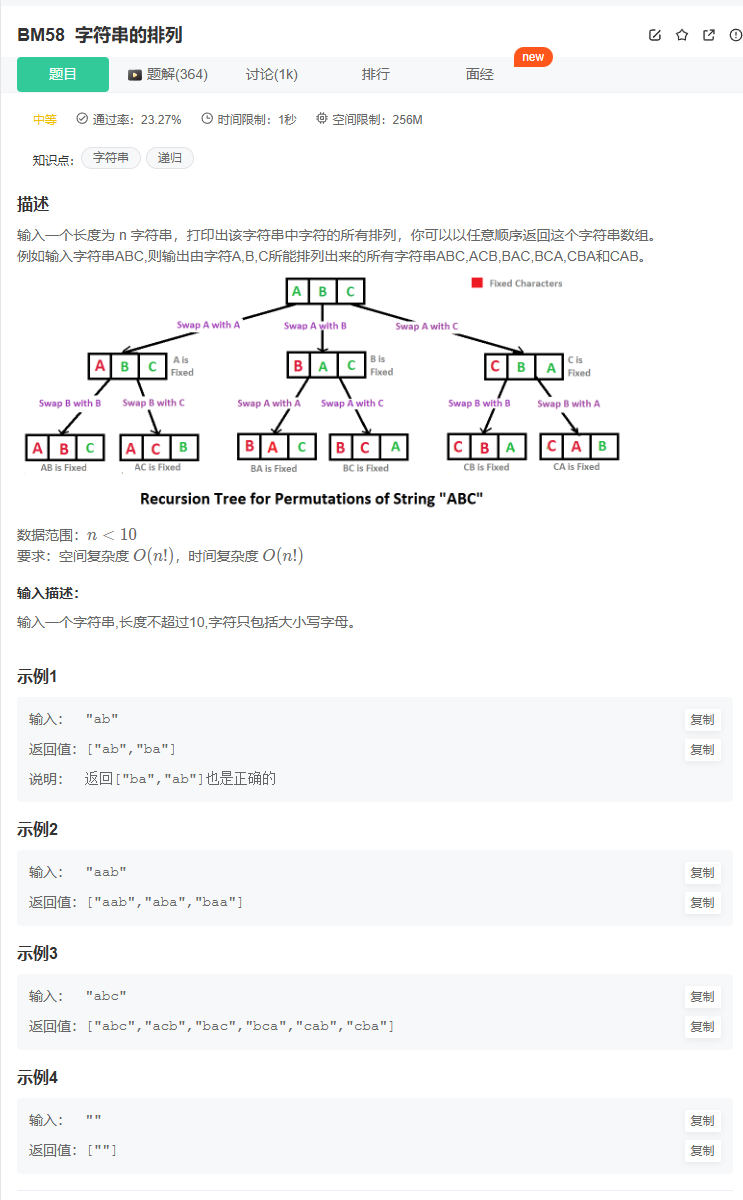
解决思路：

将字符串转为字符数组 s，便于比较处理；
使用回溯函数 dfs：
- 递归从第 start 位开始，依次与后面的字符交换，进入下一层；
- 每次递归终止于end，此时收集一个排列；
使用 unordered_set<char> 或 set<char> 控制每一层递归中已经尝试过的字符，来避免重复。
最后返回所有结果。

class Solution 
{
public:
    vector<string> Permutation(string str) 
    {
        int start = 0, end = str.length();
        set<string> tmp;
        dfs(str, tmp, start, end);

        vector<string> res;
        for(auto& s : tmp) res.push_back(s);
        return res;
        
    }

    void dfs(string& str, set<string>& tmp, int start, int end)
    {
        if(start == end) tmp.insert(str);
        else
        {
            for(int i = start; i < end; ++i)
            {
                swap(str[i], str[start]);
                dfs(str, tmp, start + 1, end);
                swap(str[i], str[start]);
            }
        }
    }
};

这个递归没太搞懂，等之后看看解析重新做一遍