Coding Practice，48天强训（31）-优快云博客

本文链接：https://blog.youkuaiyun.com/CoderPractice/article/details/147774365

Topic 1：小红的口罩（贪心、小根堆）

用最小堆来解决，这里要注意审题，口罩不是不用了就丢了，比如两个口罩一个6 一个8；第一天用6，6变成了12，但是没有丢，第二天用8，8变成了16，第三天还是可以用第一个口罩（此时变成了12的那个）

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int main() 
{
    int n, k;
    cin >> n >> k;
    vector<int> a(n);
    
    // 输入口罩的不舒适度
    for (int i = 0; i < n; ++i) cin >> a[i];
    
    // 小根堆来存储口罩的每次使用的不舒适度
    priority_queue<long long, vector<long long>, greater<long long>> pq;
    //C++ 模板不支持跳过中间模板参数单独指定后面的参数
    //priority_queue<long long, greater<long long>> pq;
    //这样写编译器会把 greater<long long> 误认为是 Container 类型
    //所以要加上vector<long long>，日常是不用写的，因为有缺省

    // 初始化小根堆
    for (int i = 0; i < n; ++i) pq.push(a[i]);

    long long td = 0;// 总忍受程度
    int days = 0;//天数
    
    // 模拟每天使用口罩的过程
    while (!pq.empty()) //pq不为空意味着还有口罩
    {
        long long d = pq.top();//堆顶是当前最干净的那个口罩
        pq.pop();//使用它，把它弹出
        
        // 如果当前不舒适度加上这个口罩的使用不超过k，意味着在忍受范围
        if (td + d <= k) 
        {
            td += d;//累加总不适程度
            days++;//能够扛过这一天
            
            // 这个口罩的下一次使用变脏，再加入队列
            pq.push(d * 2);
        } 
        else break;// 如果没有干净口罩能满足条件，无法坚持，直接跳出
    }
    
    cout << days << endl;
    return 0;
}

Topic 2：春游（枚举、边界）

春游

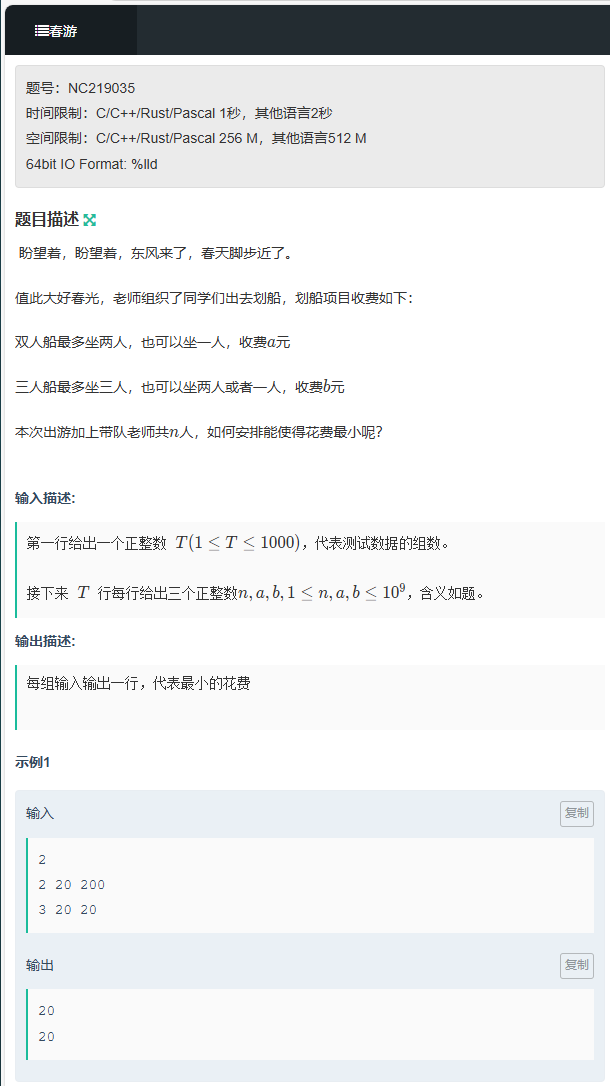
贪心问题，通过算人均成本来取舍用哪种船，如果 a / 2 < b / 3，即 3a < 2b，那么双人船的人均成本更低，我们应该尽可能多地使用双人船，反之，如果 3a > 2b，即三人船的人均成本更低，我们应该尽可能多地使用三人船。如果 3a == 2b，则两种船的人均成本相同，可以任意组合。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    int T; cin >> T;
    while (T--) 
    {
        ll n, a, b;
        cin >> n >> a >> b;

        // 如果 a / 2 < b / 3，即 3a < 2b，那么双人船的人均成本更低，我们应该尽可能多地使用双人船，
        // 反之，如果 3a > 2b，即三人船的人均成本更低，我们应该尽可能多地使用三人船。
        // 如果 3a == 2b，则两种船的人均成本相同，可以任意组合。

        ll cost = 0; // 记录花费
        if (n <= 2) cout << min(a, b) << endl;// 人数<=2，直接一条最便宜的船
        else if (3 * a <= 2 * b) // 如果双人船更划算（或成本相同）
        {
            cost = (n / 2) * a;
            if (n % 2 != 0) 
            {
                // 剩一个人
                // 要么补一个 a 或 b
                // 要么去掉一个 a，换成一个 b（即 a + b 与 b + 0）
                cost = min(cost + min(a, b), cost - a + b);
            }
            cout << cost << endl;
        }
        else // 三人船更划算
        {
            cost = (n / 3) * b;
            int rem = n % 3; // 剩下的人数

            if (rem == 1) 
            {
                // 剩一个
                // 要么多一个 a 或 b
                // 要么少一个 b，多两个 a
                cost = min(cost + min(a, b), cost - b + 2 * a);
            }
            else if (rem == 2) 
            {
                // 剩两个
                // 要么多一个 a 或 b
                // 要么少一个 b，多三个 a
                cost = min(cost + min(a, b), cost - b + 3 * a);
            }
            cout << cost << endl;
        }
    }
    return 0;
}

这题主要难点在于最后边界情况的考虑，当租2人船时，剩下1人有可能通过退1二人船加1三人船的方式来获取最小化费，三人船也是同样有两种边界情况需要考虑

Topic 3：数位染色（01背包）

数位染色_牛客题霸_牛客网

一个类01背包的题目，正好借助这个机会来复习一下01背包。

首先为什么这个题目可以用01背包的思路来解决？

我们可以把 01 背包问题想象成这样一个故事：

你有一个背包，容量是 target。
你面前有一些物品，每个物品有一个“重量”。
你要决定：每个物品要么选，要么不选（01的意思就是：选=1，不选=0），
问：你能不能恰好把背包装满？

那么回到我们的题目，我们现在有一堆数位，从这些数位里面抽一些数出来，能不能满足恰好满足一个目标，在这题里面是总数的一半，把目标数看作背包重量，每个数自身的值是每个数各自的重量，那么这不就是一个0 or 1的问题吗？很简单吧；

那么01背包问题一般用这样的dp公式来解决的：dp[i][j] = dp[i-1][j] || dp[i-1][j - arr[i]];

如果我要用前 i 个物品装满容量 j，那么有两种情况可以做到：

我不选第 i 个物品：那我就看 dp[i-1][j] 是不是 true；dp[i-1][j]都满足true了，那我dp[i][j]肯定也能true了

我选第 i 个物品：那就要求我能用前 i-1 个物品装满 j - arr[i]。最后这个arr[i]选了刚好把j填满

当两者其中任意一种情况成立，我们都认为dp[i][j]是true；

然后，我们现在已知dp[i]的状态只和dp[i - 1]的状态有关，不会受更早或者其他向量的影响，所以我们可以采用滚动数组的方式来对其进行空间优化，

那么当我们只使用一个一维数组，随着外层遍历往后走，之前的i是不是也会变成i-1？原本的i+1的位置是不是会变成新的i？是不是相当于把上一层的数据挪下来在用？形似老虎机的777滚轴，所以称为滚动数组；

我们可以举个例子，用2，2来试试看能否拼一个4出来

所以最终的代码是这样的

#include <bits/stdc++.h>
using namespace std;


string dye(string& x)
{
    int total = 0;// 记录总和
    for(auto& c : x) total += (c - '0');// 计算总和

    if (total % 2 != 0) return "No";// 如果总和是奇数，不可能平分,直接返回No

    int target = total / 2; // 我们的目标是找到一些数让他们构成总数的一半
    vector<bool> dp(target + 1, false);
    dp[0] = true;

    for(char& c : x)// 遍历物品
    {
        int d = c - '0';
        for(int j = target; j >= d; --j)//遍历容量
        {
            dp[j] = dp[j] || dp[j - d];
        }
    }
    return dp[target] ? "Yes" : "No";
}

int main() 
{
    // 01背包
    // dp[i][j] = dp[i - 1][j - arr[i]] || dp[i - 1][j] 
    string x; cin >> x;
    cout << dye(x) << endl;

    return 0;
}

这个01背包还没带上价值选项，有些题目是有重量+价值，不过也无非是加个max判断，加个value，原理都是一样的；