AtCoder Beginner Contest 351 G. Hash on Tree（树剖维护动态dp 口胡题解）

最新推荐文章于 2024-09-23 03:49:01 发布

原创最新推荐文章于 2024-09-23 03:49:01 发布 · 517 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#树链剖分 #动态dp

lca/dfs序/欧拉序/树链剖分同时被 3 个专栏收录

18 篇文章

订阅专栏

口胡题解

4 篇文章

订阅专栏

动态dp

2 篇文章

订阅专栏

本文介绍了一种使用动态规划和树链剖分的方法来处理n个节点的树形问题，通过线段树维护节点之间的关系，实现对根节点树哈希值的高效查询和修改。重点讨论了如何利用点权值变化动态维护子节点的贡献以及特殊情况下0值的处理策略。

题目

n(n<=2e5)个点，给定一个长为a的初始权值数组，

以1为根有根树，

树哈希值f计算如下：

（1）如果一个点u是叶子节点，则f[u]=a[u]

（2）否则， $f[u]=a[u]+\prod_{v\epsilon son[u]}f[v]$

q(q<=2e5)次点权修改，每次问修改之后根节点（点1）的树哈希值f

思路来源

qiuzx_代码

题解

新开一个口胡题解专栏，记录当前题目水平不在我能力范围之内

但是看别人的代码能看懂，自己写可能要调一万年的这种题，描述一下他是怎么写的

心得

动态 DP - OI Wiki

动态dp可以参考这篇，

基本是对于有根树树形dp，想动态获取根节点的dp值，dp值和树上点权相关，点权带修，

序列的动态dp，一般是线段树维护矩阵乘法（可广义换成其他运算）或线段树节点合并

树上版本，是树剖维护矩阵转移或者线段树节点

本题中，先树链剖分，求出重儿子，重链维护线段树

线段树上每个节点维护一个y=bx+a的点对(a,b)，

其中，b是f值非零的轻儿子的f积，x是重儿子的f值（未知，待代入）

a是当前节点u的a[u]值，然后就能b1*(b2x+a2)+a1这么线段树往上合并了

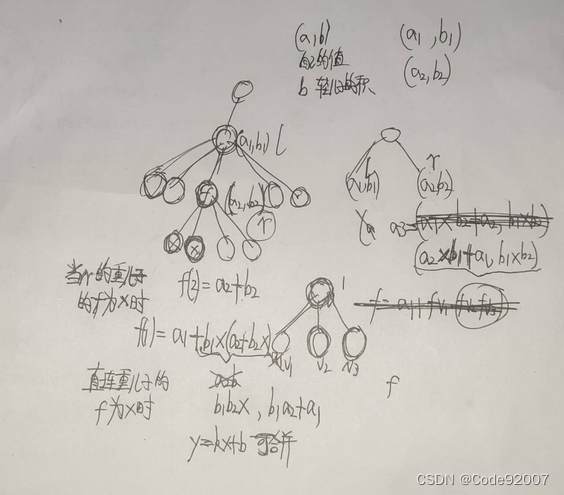
递归到叶子的时候，由于叶子不存在重儿子，x值为0，

所以链头的f值，就是当线段树区间[l,r]，

l为重链头的dfs序，r为叶子重链尾的dfs序时，这个区间节点对应的(a,b)中a的值

由于为0的值会对运算值有影响，并且儿子f值从一个0变成没有0的时候难以恢复之前的乘积，

所以单独记录0的个数，所以变更的时候，动态记录链头点的f值为0的儿子的数量

代码

qiuzx_代码

//ANMHLIJKTJIY!
#pragma GCC optimize(2)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline","fast-math","unroll-loops","no-stack-protector")
#pragma GCC diagnostic error "-fwhole-program"
#pragma GCC diagnostic error "-fcse-skip-blocks"
#pragma GCC diagnostic error "-funsafe-loop-optimizations"
#include <bits/stdc++.h>
#define INF 1000000000
#define LINF 1000000000000000000
#define MOD 1000000007
#define mod 998244353
#define F first
#define S second
#define ll long long
#define N 200010
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
char buf[1<<23],*p1=buf,*p2=buf;
ll rint(){
	ll ret=0;
	char c=getchar();
	while(!isdigit(c)) c=getchar();
	while(isdigit(c)) ret=ret*10+(c-'0'),c=getchar();
	return ret;
}
ll ksm(ll x,ll y)
{
	ll ret=1;
	while(y>0)
	{
		if(y&1)
		{
			ret=(ret*x)%mod;
		}
		x=(x*x)%mod;
		y>>=1;
	}
	return ret;
}
struct Node{
	ll a,b;
	Node(){a=b=0;}
	Node(ll _a,ll _b){a=_a,b=_b;}
	Node operator + (const Node &x)const{
		return Node((a*x.b+x.a)%mod,(b*x.b)%mod);
	}
};
struct SegT{
	ll lo[N<<2],hi[N<<2],pa[N],pb[N];
	Node val[N<<2];
	void build(ll x,ll l,ll r)
	{
		lo[x]=l,hi[x]=r;
		if(l==r)
		{
			val[x]=Node(pa[l],pb[l]);
			return;
		}
		ll mid=(l+r)>>1,a=x<<1;
		build(a,l,mid);
		build(a|1,mid+1,r);
		val[x]=val[a|1]+val[a];
		return;
	}
	void update(ll x,ll l,Node v)
	{
		ll tl=lo[x],tr=hi[x];
		if(tl==tr)
		{
			val[x]=v;
			return;
		}
		ll mid=(tl+tr)>>1,a=x<<1;
		if(mid>=l)
		{
			update(a,l,v);
		}
		else
		{
			update(a|1,l,v);
		}
		val[x]=val[a|1]+val[a];
		return;
	}
	Node query(ll x,ll l,ll r)
	{
		ll tl=lo[x],tr=hi[x];
		if(l<=tl&&tr<=r)
		{
			return val[x];
		}
		ll mid=(tl+tr)>>1,a=x<<1;
		if(mid>=r)
		{
			return query(a,l,r);
		}
		if(mid<l)
		{
			return query(a|1,l,r);
		}
		return query(a|1,l,r)+query(a,l,r);
	}
}segt;
ll n,q,fa[N],a[N],b[N],f[N],num0[N],dfn[N],dcnt=0,tp[N],lw[N],sz[N],hson[N];
vector<ll> vt[N];
void predfs(ll x)
{
	ll i;
	sz[x]=1,hson[x]=-1;
	for(i=0;i<vt[x].size();i++)
	{
		predfs(vt[x][i]);
		sz[x]+=sz[vt[x][i]];
		if(hson[x]==-1||sz[hson[x]]<sz[vt[x][i]])
		{
			hson[x]=vt[x][i];
		}
	}
	return;
}
void dfs(ll x,bool ist=true)
{
	tp[x]=ist?x:tp[fa[x]];
	dfn[x]=++dcnt;
	b[x]=1;
	if(hson[x]!=-1)
	{
		dfs(hson[x],false);
		lw[x]=lw[hson[x]];
		f[x]=f[hson[x]];
	}
	else
	{
		lw[x]=x;
		f[x]=a[x];
		return;
	}
	ll i;
	for(i=0;i<vt[x].size();i++)
	{
		if(vt[x][i]!=hson[x])
		{
			dfs(vt[x][i]);
			f[x]=(f[x]*f[vt[x][i]])%mod;
			if(f[vt[x][i]])
			{
				b[x]=(b[x]*f[vt[x][i]])%mod;
			}
			else
			{
				num0[x]++;
			}
		}
	}
	f[x]=(f[x]+a[x])%mod;
	return;
}
ll calc(ll x)
{
	Node cur=segt.query(1,dfn[x],dfn[lw[x]]);
	return cur.a;
}
int main(){
	ll i,x,y;
	n=rint(),q=rint();
	for(i=1;i<n;i++)
	{
		fa[i]=rint()-1;
		vt[fa[i]].push_back(i);
	}
	fa[0]=-1;
	for(i=0;i<n;i++)
	{
		a[i]=rint();
	}
	predfs(0);
	dfs(0);
	for(i=0;i<n;i++)
	{
		segt.pa[dfn[i]]=a[i];
		segt.pb[dfn[i]]=num0[i]?0:b[i];
	}
	segt.build(1,1,n);
	while(q--)
	{
		x=rint()-1,y=rint();
		a[x]=y;
		segt.update(1,dfn[x],Node(a[x],num0[x]?0:b[x]));
		while(true)
		{
			ll pre=f[tp[x]];
			f[tp[x]]=calc(tp[x]);
			x=tp[x];
			if(fa[x]<0)
			{
				break;
			}
			if(pre)
			{
				b[fa[x]]=(b[fa[x]]*ksm(pre,mod-2))%mod;
			}
			else
			{
				num0[fa[x]]--;
			}
			if(f[x])
			{
				b[fa[x]]=(b[fa[x]]*f[x])%mod;
			}
			else
			{
				num0[fa[x]]++;
			}
			x=fa[x];
			segt.update(1,dfn[x],Node(a[x],num0[x]?0:b[x]));
		}
		printf("%lld\n",f[0]);
	}
	return 0;
}