中国传统农历的编制

农历是阴阳历，农历中的闰月就是为了协调回归年和朔望月之间的关系。所以农历闰年时，有十三个农历月。农历以冬至朔 (十一月初一) 为一年的开始建子，中气定月序，朔日定月，定冬至，无中气置闰。

故此测定节气十分重要，古代以圭表和观星来完成此任务，所以用天文实际测量和天文演算法来定节气和朔望，农历的本质就是天文年历。

一个朔望月的平均长度是 29.53059天
一个回归年平均长度是   365.24224 天

为什么采取「十九年七闰」的方法呢？一个朔望月平均是29.53059日，一个回归年有12.368个朔望月，0.368小数部分的渐进分数是1/2 、1/3 、3/8 、4/11 、7/19 、46/125，即每二年加一个闰月，或每三年加一个闰月，或每八年加三个闰月……经过推算，十九年加七个闰月比较合适。因为十九个回归年=6939.6018日，而十九个农历年（加七个闰月后）共有235个朔望月，等于6939.68865日，两者 19 年后只相差 2 小时 5 分。

图1：2017年9月1日实施国家标准《农历的编算和颁行》

农历编算的标准主要内容：
（1）  以北京时间为标准时间；
（2）  朔日为农历月的第一个农历日；
（3）  包含节气冬至在内的农历月为农历十一月；
（4） 若从某个农历十一月开始到下一个农历十一月（不含）之间有13个农历月，则需要置闰。
          置闰规则为：取其中最先出现的一个不包含中气的农历月为农历闰月。
（5）  农历十一月之后第2个（不计闰月）农历月为农历年的起始月。

农历日期编排所依据的朔和节气时刻的计算依赖于太阳和月亮位置，按国际基本天文学规范地球自转和参考系服务规范所规定的模型计算。为了保证农历日期编排结果的唯一性，朔和节气时间的计算必须精确到在0时附近也能准确判断它们所在的农历日，根据1900年至2100年期间朔和节气时刻的计算结果，在用于日期判定时对它们的计算精度要求应达到1秒。另外，北京时间属于协调世界时，协调世界时以原子时为基准，但通过闰秒的方式与世界时时刻的偏差不超过0.9秒，闰秒由国际地球自转和参考系服务机构根据对世界时的监测来确定发布，可能在年底或年中或季末，考虑到农历需要提前一年编算发布，因此，计算精度不计及编算时尚未正式发布的闰秒。

1984年2月2日0时起到1985年2月19日24时截止的农历年为甲子年。
1949年10月1日的农历日为甲子日。

冬至月定为子月，农历年的起始月为寅月。
 

月份	月建	节气	中气	西历日期
十一月	子月	大雪	冬至	12月7/8日，12月21/22日
十二月	丑月	小寒	大寒	1月5/6日，1月20/21日
正月	寅月	立春	雨水	2月4/5日，2月19/20日
二月	卯月	惊蛰	春分	3月5/6日，3月20/21日
三月	辰月	清明	谷雨	4月4/5日，4月20/21日
四月	已月	立夏	小满	5月5/6日，5月21/22日
五月	午月	芒种	夏至	6月5/6日，6月21/22日
六月	未月	小暑	大暑	7月7/8日，7月23/24日
七月	申月	立秋	处暑	8月7/8日，8月23/24日
八月	酉月	白露	秋分	9月7/8日，9月23/24日
九月	戌月	寒露	霜降	10月8/9日，10月23/24日
十月	亥月	立冬	小雪	11月7/8日，11月22/23日

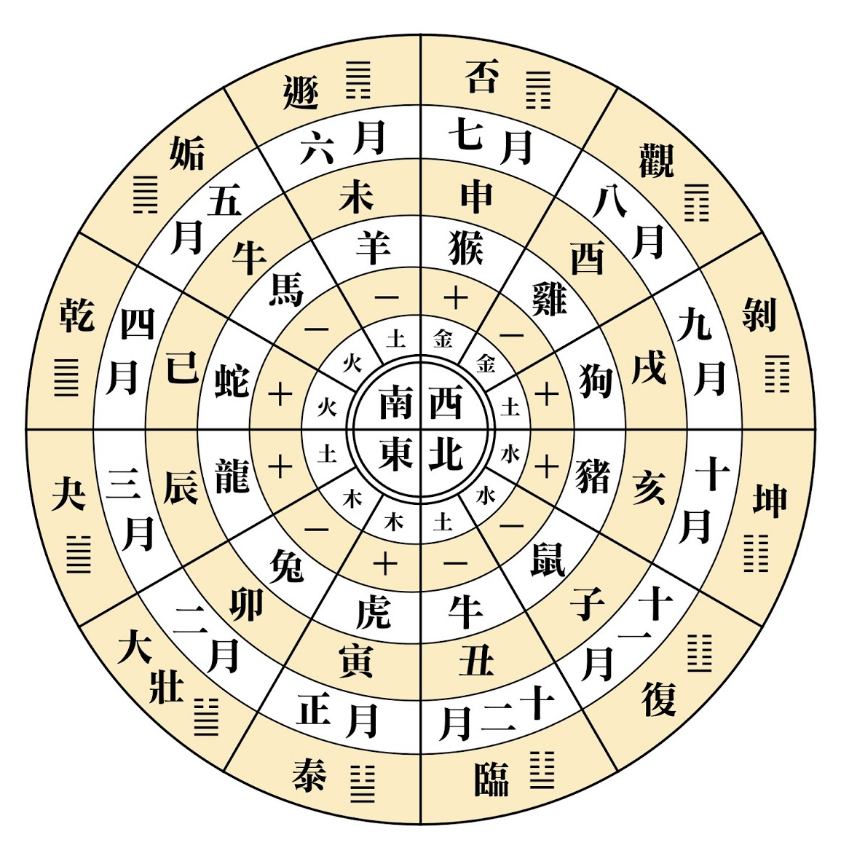
              图 2： 十二月与卦象的关系

十二辟卦

十二辟卦又称十二消息卦，或十二月卦，是指主掌一年十二个月的十二个卦。(出自西汉经学家孟喜)。
䷗   ䷒  ䷊    ䷡    ䷪   ䷀  ䷫   ䷠    ䷋  ䷓   ䷖   ䷁
复  临  泰  大壮  夬  乾  姤   遯   否  观   剥  坤

11  12  正   二    三  四  五   六  七   八   九  十

         息卦                                消卦

   (阳卦，阳长阴消)         (阴卦，阳消阴长)

举例：

复卦，十一月。「一元复始」。

十一月冬至子月，属鼠，「复」卦。「复」，阳气归来，引申为周而复始，改过迁善。「复」，意思是「回家」，《序卦》：「物不可以终尽剥，穷上反下，故受之以复。」

从卦气来看，复为十一月冬至之卦。阳气在十月坤卦被剥除到尽，为纯阴之卦，冬至十一月时阴气达到顶点，此时既是最冷也是白天最短的时候，这也是阴阳消长的转折点，阳气就是在这最冷的时候返回。从冬至之后也是白天开始渐渐变长。阳气归来，正是复卦的卦义之所在。此时也开始进入另一回合阴阳消长的循环。而冬至时虽然表面上看来是一片死寂，但却是暗藏无限生机。

「一元复始」的吉祥语就是源自于此，意指最下方一个乾元归来。只是「一元复始」正是冬至最为寒冷之时，诸事不宜，所以复卦象传说「先王以至日闭关，商旅不行，后不省方」。看来和「一元复始」比较应景的时节应是冬至吃汤圆，不是春节春暖花开。

  图 3： 《周易注疏》的复卦象传

泰卦， 正月 ， 三阳开泰。

通泰、通达。三阳开泰，阴阳融和，万事如意。

泰卦为十二辟卦中正月建寅之卦，在卦气理论中十月坤卦为阴气极盛之时，到十一月复卦一阳归来为一元复始，十二月临卦阳气开始增长，正月泰卦阳气与阴气达到最完美的均衡与调和，下卦由乾阳居内。从复到泰至乾为阳长阴消，即君子道长，小人道消的历程；从姤至遯至否一直到坤为阴长阳消。由于在「阳长阴消」历程中泰卦为第三个阳爻归来的时候，因此春节时门联常写「三阳开泰」来形容春天的来临，典故即是由此而来。

姤卦，五月。

姤为偶遇的意思，在许多古书中也会做遘或逅。金文有遘无姤，因此姤应是遘的假借，以遘为正。姤卦又有女子主事之象。就卦气来看，三月夬卦五阳处决一阴，阴气将尽，四月为乾卦纯阳，五月姤卦阴气归来，一阴在五阳之始，一阴顺承五阳。由于卦气的成长是由内向外，巽风在内为阴气向阳气侵蚀的力量，因此阴气虽然只有一爻，但其对于阳气的入侵性与破坏力，却是有如破竹，因此称「女壮」。

五月五日午时，饮菖蒲、雄黄酒，可除百病、驱百虫。例子有民间传奇《白蛇传》裡白素贞喝下雄黄酒现出原形，吓得许仙魂不附体而死。

否卦，七月。

就卦气来看，泰为春天正月建寅之卦，主生，万物兹长繁茂。否卦则是秋天七月建申之卦，主杀，万物开始凋零。阳气从复卦之后开始回来（一元复始），正月泰卦为阴阳最为调和的时候（三阳开泰），四月乾卦则是阳气增长的顶峰，到五月姤卦阴爻回来，遯卦阴气增长，到否卦则是阴阳无法交流而天地闭塞。

剥卦，十月。

就卦气的阴阳消长来看，四月乾卦阳气到顶点，之后开始阳退阴进，五月姤卦阴气归来，六月遯卦阴气增长，七月否卦大往小来，天地闭塞，八月观卦九阳大悬庙堂之上仅供观赏，至九月剥卦为五阴即将剥去最后一阳，此有如夬卦五阳将解决一阴。因此剥卦是阴气滋长几近极盛的时候，将逼退最后一阳气。得剥卦，不宜行事，应当设法避难。

农历一年一般有12个月，以 2021年为例：

2021年的朔日，由年前冬至朔日(十一月) 开始至当年冬至朔日

朔日序号	根据一般安排	朔日日期
1	十一月	15/12/2020
2	十二月	13/1/2021
3	正月	12/2/2021
4	二月	13/3/2021
5	三月	12/4/2021
6	四月	12/5/2021
7	五月	10/6/2021
8	六月	10/7/2021
9	七月	8/8/2021
10	八月	7/9/2021
11	九月	6/10/2021
12	十月	5/11/2021
	十一月	4/12/2021

共有12个朔望月，不需要置闰，但注意到十一月朔日每年差不多提前10日，累积三年便会提前一个月；换言之，每隔二至三年，冬至会移到十一月之外。

以 2023年为例：

2023年的朔日，由2022年冬至朔日(十一月) 开始至2023年冬至朔日：

朔日序号	根据一般安排	朔日日期
1	十一月	24/11/2022
2	十二月	23/12/2022
3	正月	22/1/2023
4	二月	20/2/2023
5	三月	22/3/2023
6	四月	20/4/2023
7	五月	19/5/2023
8	六月	18/6/2023
9	七月	18/7/2023
10	八月	16/8/2023
11	九月	15/9/2023
12	十月	15/10/2023
13	十一月	13/11/2023
	后十一月	13/12/2023

共有13个朔望月，2023年冬至在十一月之后，故此2023年是闰年，需要置闰月。

至于该在哪个月置闰，需要找出哪个月不含中气。

最初中气出现在阴历的月首，因为中气是根据太阳在黄经运行的轨迹，而阴历月比较阳历月短，下个月的中气逐渐向后移动，如果中气出现在阴历月的月末 (廿九或三十)，下个月出现不含中气的机会便会增加。

例如：

2023年  年前冬至     十一月廿九
                     大寒     十二月廿九
                     雨水     正月廿九
                     春分     二月三十

三月出现不含中气的机会十分大。

2023年中气及朔日表：

朔日序号	中气日期	根据一般安排	朔日日期
1	冬至 22/12  <	十一月	24/11/2022
2	大寒 20/1   <	十二月	23/12/2022
3	雨水 19/2   <	正月	22/1/2023
4	春分 21/3   <	二月	20/2/2023
5		此月不含中气	22/3/2023
6	谷雨 20/4  >=	三月	20/4/2023
7	小满 21/5	四月	19/5/2023
8	夏至 21/6	五月	18/6/2023
9	大暑 23/7	六月	18/7/2023
10	处暑 23/8	七月	16/8/2023
11	秋分 23/9	八月	15/9/2023
12	霜降24/10	九月	15/10/2023
13	小雪22/11	十月	13/11/2023
	冬至 22/12	十一月	13/12/2023

根据以上表格，发现22/3开始的朔望月，不含三月的中气谷雨，也是2023年内最先出现不含中气的月份，故此以22/3开始的朔望月定为闰月，而上一个月是二月，所以此月定为闰二月，其他月份便顺延一个月。因为置了闰二月，三月的谷雨便定为三月初一，四月中气小满定为四月初三，中气重新回到阴历的月首，开始另一个循环周期。

2033年置闰问题

朔日序号	中气日期	根据一般安排	朔日日期
1	冬至 21/12  <	十一月	3/12/2032
2	大寒 20/1   <	十二月	1/1/2032
3	雨水 18/2   <	正月	31/1/2033
4	春分 20/3   <	二月	1/3/2033
5	谷雨 20/4   <	三月	31/3/2033
6	小满 21/5   <	四月	29/4/2033
7	夏至 21/6   <	五月	28/5/2033
8	大暑 22/7   <	六月	27/6/2033
9	处暑 23/8   <	七月	26/7/2033
10		此月不含中气	25/8/2033
11	秋分 23/9  >=	八月	23/9/2033
12	霜降23/10	九月	23/10/2033
13	小雪22/11	十月	22/11/2033
	冬至 21/12	十一月	22/12/2033

根据一般坊间的历法，发现25/8开始的朔望月，不含八月的中气秋分，也是2033年内最先出现不含中气的月份，故此以25/8开始的朔望月定为闰月，而上一个月是七月，所以此月定为闰七月。可惜根据2017年9月1日实施国家标准《农历的编算和颁行》，此种置闰的方法是错误的！

原因：

朔日序号	中气日期	根据一般安排	朔日日期
1	冬至 21/12	十一月	3/12/2032
2	大寒 20/1	十二月	1/1/2032
3	雨水 18/2	正月	31/1/2033
4	春分 20/3	二月	1/3/2033
5	谷雨 20/4	三月	31/3/2033
6	小满 21/5	四月	29/4/2033
7	夏至 21/6	五月	28/5/2033
8	大暑 22/7	六月	27/6/2033
9	处暑 23/8	七月	26/7/2033
10	秋分 23/9	八月(不含中气)	25/8/2033
11	霜降23/10	九月(不含中气)	23/9/2033
12	小雪22/11	十月(不含中气)	23/10/2033
13	冬至 21/12	十一月三十	22/11/2033
			22/12/2033

你会发现，两个连续冬至之间只有12个朔望月，则根据国家标准《农历的编算和颁行》，2033年不应置闰。所以25/8开始的朔望月仍是八月，不应改为闰七月。

八月、九月、十月都没有当月中气，但冬至当日却是农历十一月三十，竟然符合冬至在十一月的要求，此种情况十分罕见，几千年才出现一次。2033年不闰，反而2034年要置闰十一月，才可以解决不含中气的问题。

因为太阳在阳历7月运动比较慢，两个中气的间隔长，最长的超过31天，在该段时间的农历月没有出现中气的可能性大，故此闰四、五、六月机会比较多，反而闰十一、十二月、正月比较少。闰十一月出现于1642, 2033, 2128, 2147, 2242, 2614；闰正月出现于 1537, 2262。

另一个较为罕见的例子是十一月初一冬至，例子有：1984 (闰十月)、2014 (闰九月) 和 2166 (闰十月)。

屈原的出生日期

维基百科定屈原出生于公元前 342年2月17日,清代学者多数推断屈原出生于公元前343年正月十四日或正月二十一日。

 图 4： 维基百科显示屈原个人资料

               图 5： 《楚辭・離騷》

屈原的《離騷》：
「帝高陽之苗裔兮，朕皇考曰伯庸。
摄提贞于孟陬兮，惟庚寅吾以降。
皇览揆余初度兮，肇锡余以嘉名。
名余曰正则兮，字余曰灵均。」

译成白话：「岁星在寅那年的孟春月，正当庚寅日那天我降生。」即是屈原出生于寅年寅月寅日。

如果把「惟庚寅吾以降」这句话，理解为屈原告诉我们，他出生的年月日都是庚寅，那么，屈原应该生于公元前331年或343年。屈原在顷襄王二十一年五月五日投江自尽，享年65岁。

屈原出生时的年干支：

-343	-342	-341	-340	-339	-338	-337	-336	-335	-334	-333	-332	-331
戊寅	己卯	庚辰	辛已	壬午	癸未	甲申	乙酉	丙戌	丁亥	戊子	己丑	庚寅

推断一：

屈原出生于公元前 331年 (楚威王九年)，庚寅年，戊寅月，庚寅日。

根据计算，楚威王九年十二月二十七日(公元前331年2月8日)庚寅年戊寅月丁已立春，丁已序号54，庚寅序号27，相差 33日。下一个庚寅日已经进入二月，故此楚威王九年正月并没有庚寅日，屈原不可能出生于公元前 331年。

                                                图 6： 公元前 331年2月月历

推断二：

屈原出生于公元前 343年，戊寅年，甲寅月，庚寅日。

根据计算，楚宣王二十七年正月十五(公元前343年2月8日)戊寅年甲寅月甲寅日立春，戊寅年甲寅月庚午日闰正月初一 (2月24日)，20天后就是庚寅日。楚宣王二十七年闰正月廿一 (公元前 343年3月16日)，当日正是「戊寅年 甲寅月 庚寅日」。因为闰正月「千年一遇」，十分罕见，兼且寅年寅月寅日出生，「三寅迭合」，最为吉祥，所以屈原父亲取其名为「正则」，字「灵均」。

                                             图 7： 公元前 343年2、3月月历

详情可参考陈玚《屈子生卒年月考》，邹汉勋《学艺斋文存》卷一《屈子生卒年月日考》，刘师培《古历管窥》。

使用Python 语言实现农历的计算

Python是目前发展最快的电脑语言，相对于其他电脑语言，Python 的优点：

(1)        最简洁
(2)        最容易学习
(3)        功能最强大
(4)        大量程序库可供使用
但 Python 的缺点就是执行较慢。

测试：

>>> import ephem
>>> hk = ephem.Observer()
>>> hk.lat, hk.lon = '22.3', '114.1'
>>> hk.date = '2023/5/5 21:00'
>>> d=hk.next_rising(ephem.Sun())
>>> print(ephem.localtime(d))
2023-05-06 05:48:35.474328
>>>

         图8：2023年5月6日香港日出日落时间

ephem 只可以计算一般天文现象，需要通过自订函数来完成农历计算任务的。

(1) 计算年干支

# 天干
gan = '甲乙丙丁戊己庚辛壬癸'
# 地支
zhi = '子丑寅卯辰巳午未申酉戌亥'
def gz_year(year):                # 返回干支纪年
      if year < 0:                      # 公元前 1年 = 天文0年
            year +=1
      year = year – 4              # 公元年份减4 (公元4年是甲子年)
      G = year % 10               # 模10，得到天干数
      Z = year % 12               # 模12，得到地支数
      return gan[G] + zhi[Z]

>>> gz_year(2023)
'癸卯'
>>> gz_year(-343)
'戊寅'
 

(2) 计算月干支

口诀：「甲己之年丙作首，乙庚之岁戊为头，丙辛寅月从庚起，丁壬壬位顺行流，更有戊癸何方发，甲寅之上好追求。」

def gz_month(year, month):             # month = 农历月份
       year = year - 3
       G = year % 10                           # 年干
       G = (G*2 + month-1) % 10        # 月干
       Z = (month + 1) % 12               # 月支
       return gan[G]+zhi[Z]

>>> gz_year(1984)
'甲子'
>>> gz_month(1984, 1)
 '丙寅'

(3) 计算日干支

因为日干支是逐日计算的，没有口诀。我们已知 1949年10月1日是甲子日，其他日子需要查万年历或用电脑计算。

(4) 计算时干支

口诀：「甲己还加甲，乙庚丙作初，丙辛从戊起，丁壬庚子居，戊癸壬为首，余辰顺序推。」

def gz_date(JD, hour):                                       # 中午时的 JD, hour 本地时
        W = (JD -11 )% 60
        G = W % 10
        Z = W % 12
        output = gan[G]+zhi[Z] + " "                       # 日干支
        G = (2*(G+1) - 2 + int(hour / 2 + 0.5) + 1 - 1) % 10
        Z = (int(hour / 2 + 0.5) + 1 - 1 ) % 12         # 时干支
        return output + gan[G]+zhi[Z]

>>> d=int(ephem.julian_date('1949-10-01')+0.5)
>>> gz_date(d, 10)
'甲子 己巳'              #1949年10月1 日上午10时 为 甲子日己巳时

(5)  三伏

三伏，夏至后第三个庚日为初伏 (共10日)，第四个庚日为中伏 (共20日)，立秋后第一个庚日为末伏 (共 10日)。

def san_fu(year):
        jd1= SolarTerms(year, 90) + 8/24             #夏至
        jd1 = int(jd1+0.5)
        count = 0
        while True:
            if ((jd1-11 ) % 60) % 10  == 6 :             #庚日
                count +=1
               if count == 3:
                    break
            jd1 += 1
        date1 = ephem.Date(jd1-0.5-2415020)   #初伏
        jd2 = jd1 + 10
        date2 = ephem.Date(jd2-0.5-2415020)   #中伏
        jd3= SolarTerms(year, 135) + 8/24          #立秋
        jd3 = int(jd3+0.5)
        while True:
            if  ((jd3-11 ) % 60) % 10 == 6 :            #庚日
                break
            jd3 += 1
        date3 = ephem.Date(jd3-0.5-2415020)  #末伏
        return date1, date2, date3

 >>> san_fu(2023)
            (45116.5, 45126.5, 45146.5)

Dublin Julian Day (都柏林儒略日)　45116.5 相当于 7月11日，45126.5 相当于 7 月21日，而末伏在 8月10日。

            验证：
            >>> ephem.Date('2023-7-11')
            45116.5
            >>> ephem.Date('2023-7-21')
            45126.5
            >>> ephem.Date('2023-8-10')
            45146.5

                                     图 9 ： 网上列出 2023年三伏天时间表

(6) 农历月份的朔日

本 Python 程序参考了以下文章：

Python公历转换农历及简易万年历

def ShuoDates(year):
  global shuo
  # 计算 14次朔日
  t0 = dzs_search(year)                        # 找十一月初一的 Dublin Julian Day
  shuo = []
  shuo.append(t0)                                 # shuo[0] 存上年冬至月朔日时刻
  for i in range (0, 14):
     t1 = ephem.next_new_moon(t0)
     shuo.append(t1)
     t0, t1 = t1, t0
 

(7) 二十四节气

def SolarTerms(year, angle):
   if angle > 270: year -= 1                    # 冬至 黄经 270 度
        if year == 0: year -= 1                   # 公元0 改为公元前1
        JD = EquinoxSolsticeJD(str(year), angle)  # 以分至点为初值
        JD1 = JD
        # 以逼近法求 JD
        while True:
                JD2 = JD1
                L = SolarLongitude(JD2)
                JD1 += math.sin(angle * math.pi / 180 - L) / math.pi * 180
                if abs(JD1 - JD2) < 0.00001:
                        break                            # 差误小于 1 秒
        return JD1 # UT

Python 程序：
求 2023年5月6日上午11:30 的农历日期和年月日時干支 (八字)。

import ephem
from datetime import date, datetime
from ephem import *
import math

def EquinoxSolsticeJD(year, angle):
        # 输入年份
        # 求分至点 JD
        if 0 <= angle < 90: 
                date = ephem.next_vernal_equinox(year)     #春分 0 度
        elif 90 <= angle < 180:
                date = ephem.next_summer_solstice(year)    #夏至 90 度
        elif 180 <= angle < 270:
                date = ephem.next_autumn_equinox(year)     #秋分 180 度
        else:
                date = ephem.next_winter_solstice(year)    #冬至  270 度
        JD = ephem.julian_date(date)
        return JD

def SolarLongitude(JD):
        # 求 JD  时的太阳黄经度数
        date = ephem.Date(JD - 2415020)
        s = ephem.Sun(date)  # date应为UT时间
        sa = ephem.Equatorial(s.ra, s.dec, epoch=date)
        se = ephem.Ecliptic(sa)
        L = se.lon / ephem.degree / 180 * math.pi
        return L

def LunarLongitude (JD):
        # 求 JD  时的月亮黄经度数
        date = ephem.Date(JD - 2415020)
        m = ephem.Moon(date)  # date应为UT时间
        ma = ephem.Equatorial(m.ra, m.dec, epoch=date)
        me = ephem.Ecliptic(ma)
        M = me.lon / ephem.degree / 180 * math.pi
        return M

def SolarTerms(year, angle):
        if angle > 270: year -= 1    #冬至 黄经 270 度
        if year == 0: year -= 1  # 公元0 改为公元前1
        JD = EquinoxSolsticeJD(str(year), angle)      # 以分至点为初值
        JD1 = JD
        # 以逼近法求 JD
        while True:
                JD2 = JD1
                L = SolarLongitude(JD2)
                JD1 += math.sin(angle * math.pi / 180 - L) / math.pi * 180
                if abs(JD1 - JD2) < 0.00001:
                        break # 差误小于 1 second
        return JD1 # UT
    
def DateCompare(JD1, JD2): # 输入UT，返回 UT+8 的比较结果
        JD1 += 0.5 + 8/24
        JD2 += 0.5 + 8/24
        if int(JD1) >= int(JD2): return True
        else: return False

def dzs_search(year): # 寻找年前冬至月朔日(UTC)
        if year == 1: year -= 1  # 公元0 改为公元前1
        dz = ephem.next_solstice(str(year-1) + '/12') # 年前冬至
        JD = ephem.julian_date(dz)
        # 可能的三种朔日 (十一月初一)
        # 冬至在近日点附近, 地球运动较快
        date1 = ephem.next_new_moon(ephem.Date(JD - 2415020 - 0))  
        JD1 = ephem.julian_date(date1)
        date2 = ephem.next_new_moon(ephem.Date(JD - 2415020 - 29)) 
        JD2 = ephem.julian_date(date2)
        date3 = ephem.next_new_moon(ephem.Date(JD - 2415020 - 31))
        JD3 = ephem.julian_date(date3)
        if DateCompare(JD, JD1): # 冬至合朔在同一日或下月 e.g. 1984 and 2014
                return date1
        elif DateCompare(JD, JD2) and (not DateCompare(JD, JD1)):   #冬至在本月(最常见)
                return date2
        elif DateCompare(JD, JD3): # 冬至在上月e.g. 2033
                return date3
  
moon = ephem.Moon()
sun = ephem.Sun()
d = ephem.now()
print ("现在 UTC: ", d)
JD = ephem.julian_date(ephem.now())
JD0 = ephem.julian_date(ephem.Date(0))
#JD0 = 2415020, JD on Dublin Julian Day
print ("Julian Day =", JD)
print ("Dublin Julian Day:", ephem.Date(0))
print ("本地时间: ", ephem.localtime(d))
d1 = ephem.next_new_moon(d)
print ("下一个朔日: ", d1)

lunar_day = ["初一","初二","初三","初四","初五","初六","初七","初八","初九","初十","十一","十二","十三","十四","十五","十六","十七","十八","十九","二十","廿一","廿二","廿三","廿四","廿五","廿六","廿七","廿八","廿九","三十"]
lunar_month = ["十一月","十二月", "正月","二月","三月","四月","五月","六月","七月","八月","九月","十月", "十一月"]
zhongji = ["大寒", "雨水", "春分", "谷雨", "小满", "夏至", "大暑", "处暑", "秋分", "霜降", "小雪", "冬至"]

print("")
# 农历计算
def ShuoDates(year):
  global shuo
  # 计算 14次朔日
  t0 = dzs_search(year)      #找十一月初一的 Dublin Julian Day
  shuo = []
  shuo.append(t0)            # shuo[0] 存上年冬至月朔日时刻
  for i in range (0, 14):
     t1 = ephem.next_new_moon(t0)
     shuo.append(t1)
     t0, t1 = t1, t0

# 西历转农历
def Solar2Lunar(d):
  global shuo
  output = ""
  parts = d.split("-")
  if d[0] == "-":
        year = - int(parts[1])
  else:
        year = int(parts[0])
  print (year, "年")
  JD1 = ephem.julian_date(d) - 8/24            # 输入日期的 JD (UTC)
  t0 = dzs_search(year+1)                      # 找今年冬至前的朔日 Dublin Julian Day
  t0JD = ephem.julian_date(t0)                 # 今年冬至前的朔日 JD
  if DateCompare(JD1, t0JD):                   #在今年冬至朔日之后, 用下一年数据
        print("Next year")       
        year = year + 1
  shuo = []                                    # 全年朔日时间 (Dublin Julian Day:)
  ShuoDates(year)
  solar_terms = []                             # 全年中气时间 (JD)
  winter_solstice1 =  EquinoxSolsticeJD(ephem.Date(str(year-1)), 270)
  winter_solstice2 =  EquinoxSolsticeJD(ephem.Date(str(year)), 270)
  solar_terms.append(winter_solstice1)
  for i in range(0, 14):
        print ("{:0>2d}".format(i), "朔日   ", ephem.Date(shuo[i]+8/24))  # 本地时间
  print()
  print ("冬至       ", ephem.Date(winter_solstice1-JD0+8/24), "十一月")
  t0JD = ephem.julian_date(shuo[13])          #冬至后第13日朔日 JD
  if DateCompare(winter_solstice2, t0JD):    # 上年冬至与下年冬至之间有13个朔日
        #print ("闰年")
        leap = 1  
  else:
        print("平年")
        leap = 0

  # 求节气
  angle = 300           # starts from 大寒 (十二月)
  for i in range(0, 12):  # 求12 个中气时刻
        t1 = SolarTerms(year, angle)
        solar_terms.append(t1)       # 中气的 JD
        print (zhongji[i], "      ", ephem.Date(t1-JD0+8/24), lunar_month[i+1])
        angle += 30
        if angle >=360:
                angle -= 360

  if leap == 1:
     # 找无中气月份
     for i in range(1, 13):                # 由十二月开始
        JD1 = solar_terms[i]
        JD1_ = int(JD1+0.5+8/24)
        JD2 = ephem.julian_date(shuo[i+1])
        JD2_ = int(JD2+0.5+8/24)
        #print (ephem.Date(JD1_-JD0), ">=", ephem.Date(JD2_-JD0), "?")
        if DateCompare(JD1, JD2):            # 中气在本月
                #print ("leap_month is ", i-1)
                leap_month = i-1
                print ("闰", lunar_month[leap_month])  # 上月份无中气, 置闰
                break

  # 求农历月份
  JD1 = ephem.julian_date(d) - 8/24
  JD1_ = int(JD1+0.5+8/24)
  for i in range(1, 14):        # starts from 1 = 十一月
    JD2 = ephem.julian_date(shuo[i])
    JD2_ = int(JD2+0.5+8/24)
    #print (ephem.Date(JD1_-JD0), "<", ephem.Date(JD2_-JD0), "?")
    if not (DateCompare(JD1, JD2)):
            print ("农历月份 = ", i)
            break
  if leap==1:
        if i < leap_month+2:
            #print (lunar_month[i-1])
            output += lunar_month[i-1]
        elif i == leap_month+2:
            #print ("闰", lunar_month[i-2])
            output += ("闰"+ lunar_month[i-2])
        else:
            #print(lunar_month[i-2])
            output += lunar_month[i-2]
  else:
        #print(lunar_month[i-1])
        output += lunar_month[i-1]

  # 求农历日
  JD2 = ephem.julian_date(shuo[i-1])
  JD2_ = int(JD2+0.5+8/24)
  #print (lunar_day[JD1_ - JD2_])
  output +=  lunar_day[JD1_ - JD2_]
  return output

#天干
gan = '甲乙丙丁戊己庚辛壬癸'
# 地支
zhi = '子丑寅卯辰巳午未申酉戌亥'

def gz_year(year):                # 返回干支纪年
      if year < 0:
            year +=1
      year = year - 3 -1          # 农历年份减3 （说明：补减1）
      G = year % 10               # 模10，得到天干数
      Z = year % 12               # 模12，得到地支数
      return gan[G] + zhi[Z]

def gz_month(year, month):  # month = 农历月份
       if year < 0:
            year +=1
       year = year - 3
       G = year % 10                   # 年干
       G = (G*2 + month-1) % 10        # 月干
       Z = (month + 1) % 12            # 月支
       return gan[G]+zhi[Z]

def gz_date(JD, hour):   # JD at noon, hour at local time 
        W = (JD -11 )% 60
        G = W % 10
        Z = W % 12
        output = gan[G]+zhi[Z] + " "
        G = (2*(G+1) - 2 + int(hour / 2 + 0.5) + 1 - 1) % 10
        Z = (int(hour / 2 + 0.5) + 1 - 1 ) % 12
        return output + gan[G]+zhi[Z]

# 输入西历日期及时间
#==========================
d = "2023-5-6 11:30"
#==========================
d_date = ephem.Date(d)
year = d_date.tuple()[0]
month = d_date.tuple()[1]
day = d_date.tuple()[2]
hour = d_date.tuple()[3]
d = str(year) + "-" + str(month) + "-" + str(day)
lunar_date = Solar2Lunar(d)
print (d , " 农历", lunar_date)
print()
angle = (month - 4)*30+15 if month > 4 else (month+8)*30+15
print (lunar_date.split("月")[0]+"月太阳黄经度数", angle)
ln_month = int((angle - 15)/30+3)
if ln_month > 12:
        ln_month -= 12
JD = int(ephem.julian_date(ephem.date(d)) + 0.5)
JD1 = int(ephem.julian_date(ephem.date(d) +0.5+8/24))     
JD2 = int(SolarTerms(year, angle) + 0.5 + 8/24)             #当月节气时刻
print (ephem.Date(JD1 - JD0), "<" , ephem.Date(JD2 - JD0),"?")
if JD1 < JD2:      # 未过节气, 当上一个月
        print ("日子在节气之前")
        ln_month = ln_month - 1
        if ln_month <=0:
                ln_month += 12
print ("农历月份 = ", ln_month)
print ("西历:", d, end='  ')
print ("时刻 = ", hour)
g_year = year             
if (month <= 2) and (ln_month >=11): 
         g_year = year - 1                      # 西历1,2月农历十一月, 十二月用上年年干求月干
if (month <= 2) and (lunar_date.find("十一月") >=0 or lunar_date.find("十二月") >=0):
         year = year - 1                         # 农历十一月, 十二月, 用上年年干
print ("年 = ", year, "月=", ln_month)
print ("年月日时干支:   ", gz_year(year)+" " + gz_month(g_year,ln_month)+" "+gz_date(JD, hour))

运行结果：

现在 UTC:  2025/9/7 17:36:48
Julian Day = 2460926.2338888887
Dublin Julian Day: 1899/12/31 12:00:00
本地时间:  2025-09-08 01:36:48
下一个朔日:  2025/9/21 19:54:04

2023 年
00 朔日    2022/11/24 06:57:12
01 朔日    2022/12/23 18:16:51
02 朔日    2023/1/22 04:53:13
03 朔日    2023/2/20 15:05:48
04 朔日    2023/3/22 01:23:06
05 朔日    2023/4/20 12:12:29
06 朔日    2023/5/19 23:53:14
07 朔日    2023/6/18 12:37:06
08 朔日    2023/7/18 02:31:46
09 朔日    2023/8/16 17:38:07
10 朔日    2023/9/15 09:39:45
11 朔日    2023/10/15 01:55:07
12 朔日    2023/11/13 17:27:22
13 朔日    2023/12/13 07:32:00

冬至        2022/12/22 05:48:00 十一月
大寒        2023/1/20 16:29:21 十二月
雨水        2023/2/19 06:34:09 正月
春分        2023/3/21 05:24:20 二月
谷雨        2023/4/20 16:13:36 三月
小满        2023/5/21 15:09:15 四月
夏至        2023/6/21 22:57:56 五月
大暑        2023/7/23 09:50:33 六月
处暑        2023/8/23 17:01:21 七月
秋分        2023/9/23 14:49:58 八月
霜降        2023/10/24 00:20:45 九月
小雪        2023/11/22 22:02:31 十月
冬至        2023/12/22 11:27:09 十一月
闰 二月
农历月份 =  6
2023-5-6  农历 三月十七

三月太阳黄经度数 45
2023/5/6 12:00:00 < 2023/5/6 12:00:00 ?
农历月份 =  4
西历: 2023-5-6  时刻 =  11
年 =  2023 月= 4
年月日时干支:    癸卯 丁巳 甲子 庚午

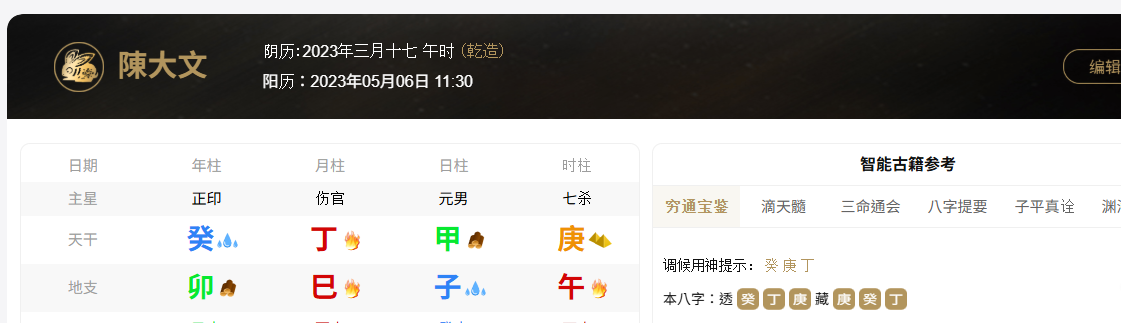
                               图 10 ： 网上查到 2023年5月6日11:30 年月日时的干支