中国古代儒家认为学生要精通「六艺」才能被称之为”士”。 这「六艺」指的是礼、乐、射、御、书、数，涵盖了古代社会所需的各种知识和技能。其中，数就是数学，古人十分重视数学，故此宋元时期，中国数学表现十分出色，涌现了一批卓越的数学家，秦九韶(约1208-1268)就是其中的杰出代表。他与李冶、杨辉和朱世杰并称“宋元数学四大家”，所著《数书九章》被誉为数学史上的经典之作。书中记载了一种算法，一般人几乎完全不理解其巧妙之处，这就是”大衍求一术”。
孙子定理
中国古代有一本书叫《孙子算经》，其中有一道题目叫做“物不知数”，原文如下：
“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？”
即问：一次不定方程
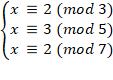
求 x 。
术曰：
三三之数剩一，则置七十; 五五之数剩一，则置二十一; 七七之数剩一，则置十五。一百六以上，以一百五减之即得。
明代程大位以一首打油诗做出完整的解答：
三人同行七十稀，五树梅花廿一枝，七子团圆月正半，除百零五便得知。
解：
x=70×2+21×3+15×2 (mod 105)
=140+63+30 (mod 105)
=233 (mod 105) = 23
为什么是 70、21、15? 所谓 ” 三三之数剩一”，即是要找一个数，它是 5 和 7 的倍数，并且被 3 除余 1，因为 5 × 7 = 35，35 ÷ 3 = 11 余 2，不合条件，而 2 × 35 = 70 符合条件，所以 ”三三之数剩一，则置 70”。同理 ”五五之数剩一，则置21”、”七七之数剩一，则置15”，求一术之名因此而来。
此方法有一定限制, 不是通解，直至南宋秦九韶的”大衍求一术”出现，才彻底解决此一问题。
大衍求一术 (中国剩余定理)
术云：
置奇右上，定居右下，立天元一于左上。先以右上除右下，所得商数与左上一相生，入左下。然后乃以右行上下以少除多，递互除之。所得商数随即递互累乘，归左行上下。须使右上末后奇一而止。乃验左上所得，以为乘率。或奇数已见单一者，便为乘率。
这一段文字太深奥，基本上无人能解，令大衍求一术逐渐失传，直至清末”西学东渐”，许多数学家尝试在中国典籍找”西学中源”的证据，才重新发现此法。
以“物不知数”为例，秦九韶的计算步骤如下：
- 求定数
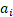：由于 3, 5, 7 互素，便为定数，省去了化约定数的步骤。 - 求衍母 M：
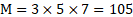。 - 求衍数
：
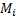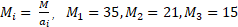。 - 求奇数
：
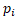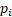满足
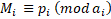的條件， 于是 
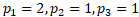。 - 求乘率
：
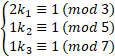
求乘率
的程序 (”大衍求一术”)：
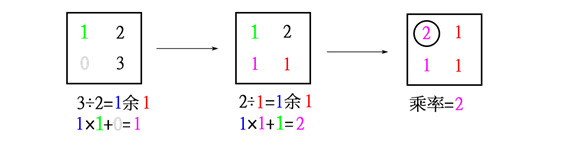
所以乘率 
=2。奇数已见单一者，便为乘率，所以
=1, 
=1 。
6. 求用数 
用数 = 乘率 × 衍数，即 
。
7.求总数N：N = 
。
8. 所求数： 
莫绍揆发表一篇论文《秦九韶大衍求一术的新研究》，用Algol 60语言编写”大衍求一术算法”，此算法记载在〈秦九韶与《数书九章》〉一书第187-188页裡 (吴文俊主编，北京师范大学出版社，1987年版)。
现改写为C++程序，以积尺寻源 (基广)为例：
即问以下同余式组：
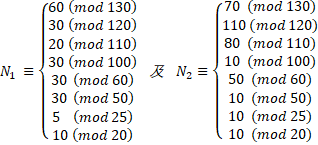
求
。
// 大衍求一术.cpp
#include <iostream>
#include <vector>
using namespace std;
int gcd(int a, int b);
int main() {
// 以积尺寻源 (基广)为例
vector<int> a = {130, 120, 110, 100, 60, 50, 25, 20};
vector<int> r = {60, 30, 20, 30, 30, 30, 5, 10};
cout << "问数 = ";
for (int num : a) cout << num << " ";
cout << endl;
cout << "余数 = ";
for (int num : r) cout << num << " ";
cout << endl;
// 求定数
int n = a.size();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int d = gcd(a[i], a[j]);
if (gcd(a[i], a[j] / d) == 1) {
a[j] /= d;
} else if (gcd(a[i] / d, a[j]) == 1) {
a[i] /= d; // 约奇不约偶，这时可反约
}
}
for (int j = i + 1; j < n; j++) {
int d = gcd(a[i], a[j]);
a[j] /= d; // 约偶, 这时必约后, 不能反约
}
}
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
while (gcd(a[i], a[j]) > 1) {
int d = gcd(a[i], a[j]);
a[i] /= d;
a[j] *= d; // 复乘求定, 循环结束时, a[i] 为定母
}
}
}
cout << "个数 = " << n << endl;
cout << "定数 = ";
for (int num : a) cout << num << " ";
cout << endl;
vector<int> m(n, 0); // 衍数
vector<int> p(n, 0); // 奇数
vector<int> k(n, 0); // 乘率
vector<int> s(n, 0); // 用数
// 求衍母
int M = 1;
for (int num : a) {
M *= num; // M 为衍母
}
cout << "衍母 = " << M << endl;
// 求衍数、奇数、乘率、用数
for (int i = 0; i < n; i++) {
m[i] = M / a[i]; // m[i] 为第 i 个衍数
p[i] = m[i];
while (p[i] > a[i]) {
p[i] -= a[i]; // p[i] 为第 i 个奇数
}
// 大衍求一术
int h2 = p[i]; // 置奇右上，
int h1 = a[i]; // 定居右下，
int e2 = 1; // 立天元一于左上
int e1 = 0;
while (h2 > 1) { // 右上末后奇一而止
if (h1 > h2) { // 右行上下以少除多
h1 -= h2;
e1 += e2;
} else if (h2 > h1) {
h2 -= h1;
e2 += e1;
}
}
k[i] = e2; // k[i] 为第 i 个乘率
s[i] = k[i] * m[i]; // s[i] 为第 i 个用数
}
cout << "衍数 = ";
for (int num : m) cout << num << " ";
cout << endl;
cout << "奇数 = ";
for (int num : p) cout << num << " ";
cout << endl;
cout << "乘率 = ";
for (int num : k) cout << num << " ";
cout << endl;
cout << "用数 = ";
for (int num : s) cout << num << " ";
cout << endl;
int N = 0;
for (int i = 0; i < n; i++) {
N += r[i] * s[i];
}
cout << "总数 = " << N << endl;
N = N % M; // N 即所求数
cout << "所求数 = " << N << endl;
return 0;
}
// 求 a, b最大公约数
int gcd(int a, int b) {
while (b) {
int temp = a % b;
a = b;
b = temp;
}
return a;
}
运行结果：
问数 = 130 120 110 100 60 50 25 20
余数 = 60 30 20 30 30 30 5 10
个数 = 8
定数 = 13 24 11 25 1 1 1 1
衍母 = 85800
衍数 = 6600 3575 7800 3432 85800 85800 85800 85800
奇数 = 9 23 1 7 1 1 1 1
乘率 = 3 23 1 18 1 1 1 1
用数 = 19800 82225 7800 61776 85800 85800 85800 85800
总数 = 12099030
所求数 = 1230 (广1丈2尺3寸)
后话:
定数是1，可以省略不计, 故原同余式组可以简化为:
问数 = 130 120 110 100
余数 = 60 30 20 30
个数 = 4
定数 = 13 24 11 25
衍母 = 85800
衍数 = 6600 3575 7800 3432
奇数 = 9 23 1 7
乘率 = 3 23 1 18
用数 = 19800 82225 7800 61776
总数 = 5664030
所求数= 1230
扫一扫
2134
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
