STC32G12K128计算e常数精确到小数点后19,720位的C程序

本人曾用汇编语言写一个程序计算e 常数精确到小数点后19,720位，后来尝试把它转为C语言遇到两大难题：

运用位运算执行任意精度除法。
执行任意精度乘法把常数e 由2进制小数转为10进制小数。

舍难取易，最初用10进制计算至 8192 个小数位，比起原先的19,720位少了很多。然后再思考如何尽用STC32G12K128 单片机 xdata 内的8K SRAM？使用2进制有 19726位，而10进制却只有 8196位，浪费了很多存储空间！

如果运用C程序位运算逐一处理2进制位元，预料過程十分繁琐及耗时，改用10进制则简化了计算兼且直观，但占用较多存储空间，可否改用其他进制呢？须知道：进制愈大，效率愈高。

最后，决定用256进制编写以下C程序：

第一难题

这个函数的目的是实现任意精度的除法运算，即将一个多字节大数（以256为基数表示）除以一个16位元小数（d），并将结果存储回原数组 x 中。通过使用256进制，你可以在一个字节内处理8位二进制数，从而简化了计算过程。

// 任意精度除法
// x = x / d
void Div(unsigned char *x, unsigned int d)
{
   unsigned int i, q, carry=0;
unsigned long xi;
   for (i=0; i<8192; i++) {
   xi = x[i]+carry*256L;       // carry 最大值是0xFFFE, xi最大值是 0xFFFEFF
   q = xi/d ;
   carry = xi-q*d ; // 此动作比 % 快
x[i] = q; // q最大值是 0xFF
}
}

假设q最大值是 0xFF (10进制 255)，今用 Excel 模拟 Div 子程序，因为 257 × 255 = 65535，故此 (1+256^-1)÷257 = 1/256 = 0.00390625, 有机会出现 q 最大值 255。

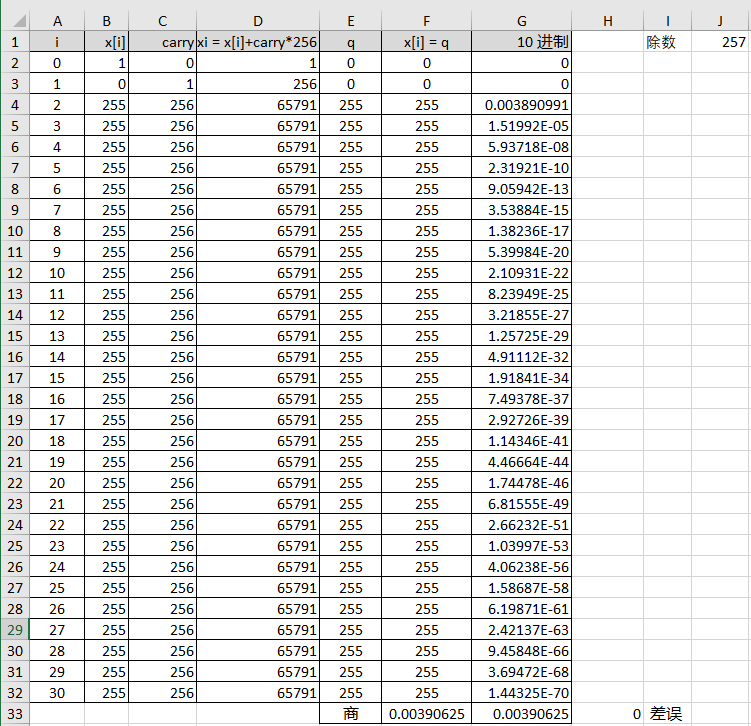
为了证实此假设的真确性, 本人运行了以下C++ 程序找出所有除数裡 xi, carry, q 的最大值，：

#include <stdio.h>
#define SIZE 8192	  	
#define DIV_START 65535

unsigned long CARRY_MAX=0, XI_MAX=0, Q_MAX=0;
unsigned char e[SIZE];    

void clear(unsigned char digits[]) {
    int i;
    for (i = 0; i < SIZE; i++) {
       digits[i] = 0; 	 
    }
}

void Div(unsigned char x[], unsigned int d) 
{
      unsigned int i, q;
      unsigned long carry=0, xi;
      for (i=0; i<SIZE; i++) {
            xi    = x[i]+carry*256L;
            q     = xi/d ;            
            carry = xi-q*d ;
            x[i]  = q;
            if (xi > XI_MAX)       XI_MAX = xi;
            if (carry > CARRY_MAX) CARRY_MAX=carry;
            if (q > Q_MAX)         Q_MAX= q;
      } 
}

int main(){
    int divisor;
    clear(e);
    for (divisor=DIV_START; divisor>1; divisor--)
    {
        e[0]++;
        Div(e, divisor);
    }
    printf("Max xi= 0x%LX\r\n", XI_MAX);
    printf("Max carry= 0x%LX\r\n", CARRY_MAX);
    printf("Max q= 0x%LX\r\n", Q_MAX);
    return(0);
}

运行结果：

Max xi= 0xFFF5A9
Max carry= 0xFFF5
Max q= 0xFF

由此证明，假设正确。不需要声明 unsigned long carry，可以加快运行速度。

第二难题

這个函数的目的是将一个多字节大数（以256为基数表示）乘以一个小整数 m，并将结果存储回数组 x 中。乘法过程中考虑了进位（carry），确保每个字节的计算结果正确。

// 任意精度乘法
// x = x*m.
unsigned int Mul (unsigned char *x, unsigned int m)
{
unsigned int i, carry=0;