本文深入探讨了齐次坐标、坐标变换、相机模型、单应矩阵与常见投影变换等核心概念，详细解析了等距变换、相似变换、仿射变换及射影变换，并介绍了针孔相机模型、透视相机模型以及双视图几何中的对极几何和基础矩阵。
摘要： 本文来自章国峰_相机模型与投影变换ppt总结，补充了自己的对于多视图几何的一些理解，图来自ppt。
一、 齐次坐标和坐标变换（等距变换；相似变换；仿射变换；射影变换）
1. 齐次坐标：
在原有的坐标上面增加一个维度，新增维度不增加自由度，通常为1
以下对应2维和3维
[xy]\begin{bmatrix}x \\ y \end{bmatrix}[xy]变为[xy1]\begin{bmatrix}x \\ y \\1 \end{bmatrix}⎣⎡xy1⎦⎤ ， [xyz]\begin{bmatrix}x \\ y \\z \end{bmatrix}⎣⎡xyz⎦⎤变为[xyz1]\begin{bmatrix}x \\ y \\z \\1 \end{bmatrix}⎣⎢⎢⎡xyz1⎦⎥⎥⎤
A. 齐次坐标可以更好的表示平移和放缩，旋转和平移
使用齐次坐标完成平移和放缩
[u′v′1]=[su0sutu0svsvtv001][uv1]=[su000sv0001][10tu01tv001][uv1]=STx\begin{bmatrix}{u}' \\{v}' \\1 \end{bmatrix}=\begin{bmatrix}s_{u} &0 &s_{u}t_{u}
\\0 &s_{v} &s_{v}t_{v}
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}u
\\v
\\1
\end{bmatrix}=\begin{bmatrix}s_{u} &0 &0
\\0 &s_{v} &0
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}1 &0 &t_{u}
\\0 &1 &t_{v}
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}u
\\v
\\1
\end{bmatrix}=
STx⎣⎡u′v′1⎦⎤=⎣⎡su000sv0sutusvtv1⎦⎤⎣⎡uv1⎦⎤=⎣⎡su000sv0001⎦⎤⎣⎡100010tutv1⎦⎤⎣⎡uv1⎦⎤=STx
使用齐次坐标完成旋转和放缩
[u′v′1]=[cos(θ)−sin(θ)tusin(θ)cos(θ)tv001][uv1]=[10tu01tv001][cos(θ)−sin(θ)0sin(θ)cos(θ)0001][uv1]=TRx\begin{bmatrix}{u}' \\{v}' \\1 \end{bmatrix}=
\begin{bmatrix}cos(\theta) &-sin(\theta) &t_{u}
\\sin(\theta) &cos(\theta) &t_{v}
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}u
\\v
\\1
\end{bmatrix}=
\begin{bmatrix}1 &0 &t_{u}
\\0 &1 &t_{v}
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}cos(\theta) &-sin(\theta) &0
\\sin(\theta) &cos(\theta) &0
\\0 &0 &1
\end{bmatrix}
\begin{bmatrix}u
\\v
\\1
\end{bmatrix}=
TRx⎣⎡u′v′1⎦⎤=⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0tutv1⎦⎤⎣⎡uv1⎦⎤=⎣⎡100010tutv1⎦⎤⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤⎣⎡uv1⎦⎤=TRx
B. 并且可以用齐次坐标更容易表示点，线，面的关系。可以用两个齐次坐标的点的叉积描述一条直线，两条线的叉积定义一个点（交点）
l=p×ql=p \times ql=p×q
x=p×qx=p \times qx=p×q
C(补充). 引入齐次坐标后，可以很好的表示以下两种概念（2D下表示）：
理想点：[x1x20]\begin{bmatrix}x_{1}&x_{2}&0 \end{bmatrix}[x1x20]表示理想点，或者无穷远点。通过引入理想点，我们可以表示两平行直线的交点。
无穷远线：上述理想点的集合，即为无穷远线，用矢量l=[001]Tl=\begin{bmatrix}0 &0&1 \end{bmatrix}^{T}l=[001]T表示
D. 向量叉积的矩阵表示
v×xv\times xv×x 表示向量的叉积，与下面这种矩阵乘法等价，所以我们可以用矩阵的线性乘法来表示叉积
v×x=[v]×xv\times x=[v]_{\times}xv×x=[v]×x
其中[v]×=[0−vzvzvz0−vx−vyvx0][v]_{\times}=
\begin{bmatrix}0 &-v_{z} &v_{z}
\\v_{z}&0&-v_{x}
\\-v_{y}&v_{x}&0\end{bmatrix}[v]×=⎣⎡0vz−vy−vz0vxvz−vx0⎦⎤,其是秩为2的3×33\times33×3的斜对称矩阵。
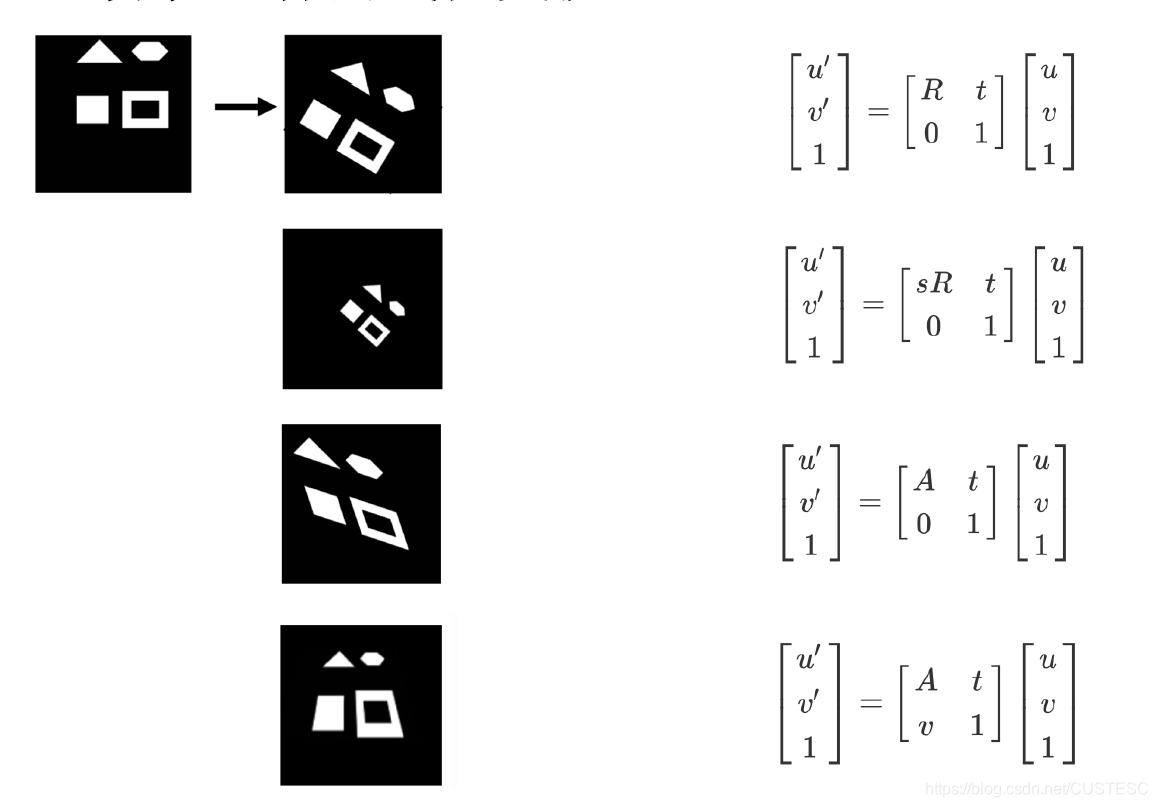
2. 几种变换（2D下描述）
A. 等距变换：2D变换有三个自由度，是保距离的
[u′v′1]=[Rt01][uv1]\begin{bmatrix}{u}' \\{v}' \\1\end{bmatrix}=\begin{bmatrix}R&t
\\0&1\end{bmatrix}
\begin{bmatrix} u\\v\\1\end{bmatrix}⎣⎡u′v′1⎦⎤=[R0t1]⎣⎡uv1⎦⎤
B. 相似变换：2D情况具有四个自由度，保角度（等距变换上，多了放缩因子s）
[u′v′1]=[sRt01][uv1]\begin{bmatrix}{u}' \\{v}' \\1\end{bmatrix}=\begin{bmatrix}sR&t
\\0&1\end{bmatrix}
\begin{bmatrix} u\\v\\1\end{bmatrix}⎣⎡u′v′1⎦⎤=[sR0t1]⎣⎡uv1⎦⎤
C. 仿射变换：六自由度，保平行
[u′v′1]=[At01][uv1]\begin{bmatrix}{u}' \\{v}' \\1\end{bmatrix}=\begin{bmatrix}A&t
\\0&1\end{bmatrix}
\begin{bmatrix} u\\v\\1\end{bmatrix}⎣⎡u′v′1⎦⎤=[A0t1]⎣⎡uv1⎦⎤
A=[a11a12a21a22]=R(θ)R(−ϕ)SR(ϕ)A=\begin{bmatrix}a_{11}&a_{12}
\\a_{21}&a_{22}\end{bmatrix}=R(\theta)R(-\phi)SR(\phi)A=[a11a21a12a22]=R(θ)R(−ϕ)SR(ϕ) S=[sx00sy]S=\begin{bmatrix}s_{x}&0
\\0&s_{y}\end{bmatrix}S=[sx00sy]
D. 射影变换：八自由度，保同线性
[u′v′1]=[Atvb]=[uv1]\begin{bmatrix}{u}' \\{v}' \\1\end{bmatrix}=\begin{bmatrix}A&t
\\v&b\end{bmatrix}=
\begin{bmatrix} u\\v\\1\end{bmatrix}⎣⎡u′v′1⎦⎤=[Avtb]=⎣⎡uv1⎦⎤ H=[Atvb]H=\begin{bmatrix}A&t
\\v&b\end{bmatrix}H=[Avtb]
求解射影变换(下面有八个未知数，需要四组点来求解)：
H=[Atvb]=[h1h2h3h4h5h6h7h8h9]H=\begin{bmatrix}A&t
\\v&b\end{bmatrix}=
\begin{bmatrix}h_{1}&h_{2}&h_{3}
\\h_{4}&h_{5}&h_{6}
\\h_{7}&h_{8}&h_{9}\end{bmatrix}H=[Avtb]=⎣⎡h1h4h7h2h5h8h3h6h9⎦⎤ x′=Hx{x}'=Hxx′=Hx
展开上述关于u_{2}和v2v_{2}v2的等式：
h1u1+h2u2+h3−h7u1u2−h8v1u2−h9u2=0h_{1}u_{1}+h_{2}u_{2}+h_{3}-h_{7}u_{1}u_{2}-h_{8}v_{1}u_{2}-h_{9}u_{2}=0h1u1+h2u2+h3−h7u1u2−h8v1u2−h9u2=0
h4u1+h5u2+h6−h7u1v2−h8v1v2−h9v2=0h_{4}u_{1}+h_{5}u_{2}+h_{6}-h_{7}u_{1}v_{2}-h_{8}v_{1}v_{2}-h_{9}v_{2}=0h4u1+h5u2+h6−h7u1v2−h8v1v2−h9v2=0
改写为：
Ai=(u1v11000−u1u2−v1u2−u2000u2v21u1v2−v1v2−v2)A_{i}=\begin{pmatrix}u_{1}&v_{1}&1&0&0&0&-u_{1}u_{2}&-v_{1}u_{2}&-u_{2}
\\0&0&0&u_{2}&v_{2}&1&u_{1}v_{2}&-v_{1}v_{2}&-v_{2}\end{pmatrix}Ai=(u10v10100u20v201−u1u2u1v2−v1u2−v1v2−u2−v2)
h∗=(h1h2h3h4h5h6h7h8h9)h^{*}=\begin{pmatrix}h_{1}&h_{2}&h_{3}&h_{4}&h_{5}&h_{6}&h_{7}&h_{8}&h_{9}\end{pmatrix}h∗=(h1h2h3h4h5h6h7h8h9)
改写为： Aih=0A_{i}h=0Aih=0
总结：
二、 相机模型
1. 针孔相机模型（如下图）
世界坐标系中的点到针孔相机像平面变换为
(fXfYZ)=[ff1][101010](XYZ1)\begin{pmatrix}fX\\fY\\Z\end{pmatrix}=\begin{bmatrix}f\\&f\\&&1\end{bmatrix}\begin{bmatrix}1&&&0\\&1&&0\\&&1&0\end{bmatrix}\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}⎝⎛fXfYZ⎠⎞=⎣⎡ff1⎦⎤⎣⎡111000⎦⎤⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
KKK [R∣t][R|t][R∣t]
KKK为相机内参矩阵； [R∣t][R|t][R∣t]为旋转位移矩阵
由于装调等误差，存在主点的偏移:
(fX/Z+x0fY/Z+x01)\begin{pmatrix}fX/Z+x_{0}\\fY/Z+x_{0}\\1\end{pmatrix}⎝⎛fX/Z+x0fY/Z+x01⎠⎞~(fX+Zx0fY+Zx0Z)=[fx00fy0010](XYZ1)\begin{pmatrix}fX+Zx_{0}\\fY+Zx_{0}\\Z\end{pmatrix}=\begin{bmatrix}f&&x_{0}&0\\&f&y_{0}&0\\&&1&0\end{bmatrix}\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix}⎝⎛fX+Zx0fY+Zx0Z⎠⎞=⎣⎡ffx0y01000⎦⎤⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
透视相机模型,其内参矩阵增加了一个扭曲因子s：
K=[fsx0fy01]K=\begin{bmatrix}f&s&x_{0}\\&f&y_{0}\\&&1\end{bmatrix}K=⎣⎡fsfx0y01⎦⎤
径向畸变：设畸变量为R(x,y)R(x,y)R(x,y)，则R(x,y)=(1+k1r2+k2r4+...)R(x,y)=(1+k_{1}r^{2}+k_{2}r^{4}+...)R(x,y)=(1+k1r2+k2r4+...)
2. 相机外参（旋转和平移）
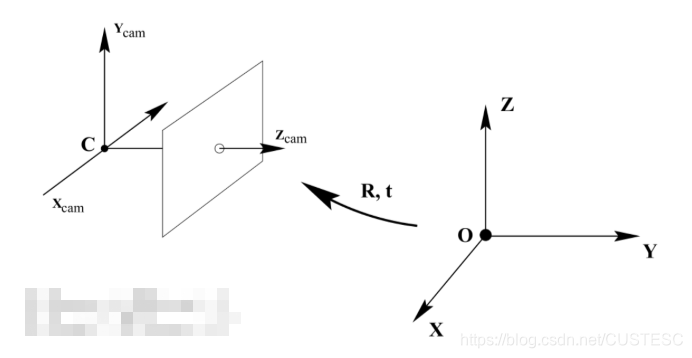
相机坐标和世界坐标的转换关系为{Xc=RXw+tXw=R′Xc+t′\left\{\begin{matrix}X_{c}=RX_{w}+t
\\X_{w}=R^{'}X_{c}+t^{'}
\end{matrix}\right.{Xc=RXw+tXw=R′Xc+t′，其中{R′=R−1t′=−R−1t\left\{\begin{matrix}R^{'}=R^{-1}
\\t^{'}=-R^{-1}t
\end{matrix}\right.{R′=R−1t′=−R−1t。
三、单应矩阵与常见投影变换
1. 单应矩阵
这里描述了一副图像，经过纯旋转后得到的图像，其中共有的点可以用以上矩阵关系描述，这个矩阵称为单应矩阵，H可以表示为H=K2RK1−1H=K_{2}RK_{1}^{-1}H=K2RK1−1。使用点来表示H形成的对应关系，可以是
c(u2v21)=(h1h2h3h4h5h6h7h8h9)(u1v11)c\begin{pmatrix}u_{2}
\\v_{2}
\\1
\end{pmatrix}=\begin{pmatrix}h_{1}&h_{2}&h_{3}
\\h_{4}&h_{5}&h_{6}
\\h_{7}&h_{8}&h_{9}
\end{pmatrix}\begin{pmatrix}u_{1}
\\v_{1}
\\1
\end{pmatrix}c⎝⎛u2v21⎠⎞=⎝⎛h1h4h7h2h5h8h3h6h9⎠⎞⎝⎛u1v11⎠⎞
其中(u2v21)\begin{pmatrix}u_{2}
\\v_{2}
\\1
\end{pmatrix}⎝⎛u2v21⎠⎞和(u1v11)\begin{pmatrix}u_{1}
\\v_{1}
\\1
\end{pmatrix}⎝⎛u1v11⎠⎞分别表示第二幅图和第一幅图中对应点的坐标。
2. 平面投影变换
选择一个世界坐标系，使得平面上的点在该坐标系下Z坐标为0，可以推导投影矩阵
(x1x2x3)=(p11p12p13p14p21p22p23p24p31p32p33p34)=(XY01)=(p11p12p14p21p22p24p31p32p34)(XY1)\begin{pmatrix}x_{1}
\\x_{2}
\\x_{3}
\end{pmatrix}=\begin{pmatrix}p_{11}&p_{12}&p_{13}&p_{14}
\\p_{21}&p_{22}&p_{23}&p_{24}
\\p_{31}&p_{32}&p_{33}&p_{34}
\end{pmatrix}=\begin{pmatrix}X
\\Y
\\0
\\1
\end{pmatrix}=\begin{pmatrix}p_{11}&p_{12}&p_{14}
\\p_{21}&p_{22}&p_{24}
\\p_{31}&p_{32}&p_{34}
\end{pmatrix}\begin{pmatrix}X
\\Y
\\1
\end{pmatrix}⎝⎛x1x2x3⎠⎞=⎝⎛p11p21p31p12p22p32p13p23p33p14p24p34⎠⎞=⎝⎜⎜⎛XY01⎠⎟⎟⎞=⎝⎛p11p21p31p12p22p32p14p24p34⎠⎞⎝⎛XY1⎠⎞
这个矩阵描述了三维平面到图像平面的射影变换：
A.使用透视相机时，最常见的一种从世界坐标系到图像平面的变换
B.两平面的映射用该3*3的矩阵表示
C.射影变换通常也称为“单应性映射”
D.H有八个自由度
3. 其它变换
弱透视变换：景物平面到相机面坐标是是比例关系
正交投影：两平面坐标大小相等，符号相反
四、双视图几何
1. 对极几何
对极几何是两视图之间满足的关系，指两幅视图上对应的点满足：
x′Fx=0x^{'}Fx=0x′Fx=0
这里的矩阵F，称为基础矩阵(Fundamental matrix)。
2. 求解基础矩阵F
第一次更新：19.11.15 15：50
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
