矩阵指数
矩阵指数是方块矩阵的一种矩阵函数,与指数函数类似。矩阵指数给出了矩阵李代数与对应的李群之间的关系。
设X为n×n的实数或复数矩阵。X的指数,用eX或exp(X)来表示,是由以下幂级数所给出的n×n矩阵:
以上的级数总是收敛的,因此X的指数是定义良好的。注意,如果X是1×1的矩阵,则X的矩阵指数就是由X的元素的指数所组成的1×1矩阵。
目录
性质
设X和Y为n×n的复数矩阵,并设a和b为任意的复数。我们把n×n的单位矩阵记为I,把零矩阵记为0。矩阵指数满足以下性质:
- e0 = I。
- eaXebX = e(a + b)X。
- eXe−X = I。
- 如果XY = YX,则eXeY = eYeX = e(X + Y)。
- 如果Y是可逆的,则eYXY−1 = YeXY−1。
- det(eX) = etr(X),其中tr(X)是X的迹数。
- exp(XT) = (exp X)T,其中XT表示X的转置。从中可以推出,如果X是对称矩阵,则eX也是对称矩阵;如果X是斜对称矩阵,则eX是正交矩阵。
- exp(X*) = (exp X)*,其中X*表示X的共轭转置。可以推出,如果X是埃尔米特矩阵,则eX也是埃尔米特矩阵;如果X是斜埃尔米特矩阵,则eX是酉矩阵。
线性微分方程
矩阵指数的一个重要性,是它可以用来解微分方程。从(1)可知,以下微分方程
其中A是矩阵,具有解
矩阵指数也可以用来解非齐次方程:
参见以下的例子。
当A不是常数时,以下形式的微分方程没有闭式解:
但马格努斯级数可以给出无穷级数形式的解。
指数相加
我们知道,对于任何实数(标量)x和y,指数函数都满足公式ex + y = exey。类似的等式对于可交换矩阵也成立:如果矩阵X和Y是可交换的(意思是说XY = YX),则:
但是,如果它们不是可交换的,则以上的等式不一定成立。在这种情况下,我们可以用Baker-Campbell-Hausdorff公式来计算eX + Y。
这个命题反过来不成立:eX + Y = eXeY并不一定就意味着X和Y是可交换的。但是,如果X和Y只含有代数数,而且它们的大小至少为2×2,则反过来也成立。 (Horn & Johnson 1991,pp.435–437).
指数映射
注意矩阵的指数总是非奇异方阵。eX的逆矩阵由e−X给出。这与复数的指数总是非零的事实类似。这样,矩阵指数就给出了一个映射:
这是从所有n×n矩阵的空间到一般线性群(所有非奇异方阵所组成的群)的映射。实际上,这个映射是满射,就是说每一个非奇异方阵都可以写成某个矩阵的指数。矩阵对数就是这个映射的逆映射。
对于任何两个矩阵X和Y,我们有:
其中|| · ||表示任意的矩阵范数。从中可以推出,指数映射在Mn(C)的紧子集内是连续和利普希茨连续的。
以下的映射
定义了一般线性群中的一条光滑曲线,当t = 0时穿过单位元。实际上,这给出了一般线性群的一个单参数子群,这是由于:
这条曲线在点t的导数(或切向量)由以下等式给出:
t = 0时的导数就是矩阵X,所以我们可以说,X是这个单参数子群的推广。
更加一般地:
矩阵指数的计算
寻找计算矩阵指数的可靠和准确的方法是困难的,目前在数学和数值分析领域中仍然是一个正在研究的话题。有些方法列举如下。
可对角化矩阵
如果矩阵是对角的:
则把主对角线上的所有元素取指数,就是原矩阵的指数:
这也允许了我们计算可对角化矩阵的指数。如果 ,且D是对角矩阵,则
,且D是对角矩阵,则 。用西尔维斯特公式,也可以得到相同的结果。
。用西尔维斯特公式,也可以得到相同的结果。
幂零矩阵
如果对于某个整数q,有Nq = 0,则矩阵N称为幂零矩阵。在这种情况下,矩阵指数eN可以直接从级数展开式来计算,这是因为级数在有限个项后就终止了:
推广
当矩阵X的最小多项式可以分解为一次多项式的积时,它就可以表示为以下的和:
其中:
- A是可对角化矩阵;
- N是幂零矩阵;
- A与N是可交换的(也就是说, AN = NA)。
这称为Dunford分解。
这就是说,我们可以通过化为前两种情况,来计算X的指数:
注意为了让最后一步成立, A和N必须是可交换的。
另外一个密切相关的方法,是利用X的若尔当标准型。假设X = PJP −1,其中J是X的若尔当标准型。那么:
另外,由于
因此,我们只需要知道怎样计算若尔当块的矩阵指数。但是,每一个若尔当块都具有形式
其中N是幂零矩阵。则这个区块的矩阵指数由下式给出:
计算
假设我们想要计算以下矩阵的指数。
它的若尔当型为:
其中矩阵P由下式给出:
我们首先来计算exp(J)。我们有:
1×1矩阵的指数仅仅是该矩阵的元素的指数,因此exp(J1(4)) = [e4]。 的指数可以用以上提到的公式exp(λ
的指数可以用以上提到的公式exp(λ +N) = eλ exp(N)来算出:
+N) = eλ exp(N)来算出:
因此,原矩阵B的指数为:
应用
线性微分方程
矩阵指数在解线性微分方程时十分有用。前面曾提到,以下形式的微分方程
具有解eCty(0)。如果我们考虑以下向量
我们就可以把线性微分方程表示为:
如果我们作一个猜想,把两边乘以一个积分因子 e−At,便得到:
如果我们可以计算eAt,那么就得到了微分方程的解。
例子(齐次)
假设我们有以下的微分方程组:
相关的矩阵为:
在以上的例子中,我们计算了矩阵指数
因此微分方程组的通解为:
也就是说,
非齐次的情况──参数变换
对于非齐次的情况,我们可以用积分因子的方法(类似于参数变换的方法)。我们找到形为yp(t) = exp(tA)z(t)一个特解:
为了让yp为方程的解,必须有:
因此,
其中c由问题的初始条件决定。
例子(非齐次)
假设我们有以下的微分方程组:
那么我们有
以及
用前面的方法,我们可以得出齐次微分方程的解。由于齐次方程的通解与非齐次方程的特解的和就是非齐次方程的通解,因此我们只需要找到一个特解(用参数变换法)。
我们有:
进一步简化,就可以得到原方程的特解。






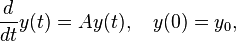







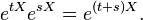







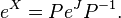
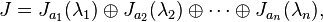
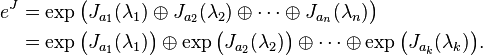




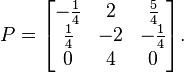



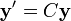



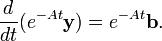

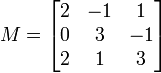



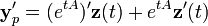


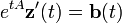
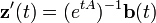





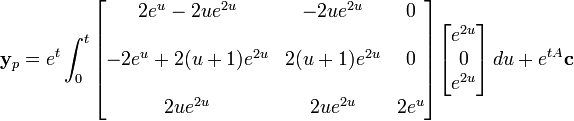


















 7336
7336










