小白的深度学习日常7

深度学习

一、感知机

感知机介绍

感知机（Perceptron）是一种简单的人工神经网络模型，由美国心理学家弗兰克·罗森布拉特（Frank Rosenblatt）在1957年提出，在机器学习和人工智能领域具有重要地位，是理解更复杂神经网络的基础。以下从原理、算法过程、应用场景、优缺点等方面进行介绍：

原理

• 基本概念：感知机是一种二分类的线性分类模型，它将输入特征通过权重向量进行加权求和，再经过一个激活函数（通常为阶跃函数）来判断输入样本属于哪一类。可以将其看作是一个简单的“逻辑判断单元”，根据输入信息做出类别决策。
• 数学模型：假设输入向量为$x=(x_1,x_2,\cdots ,x_n)$，对应的权重向量为$w=(w_1,w_2,\cdots ,w_n)$，偏置为$b$。首先计算净输入$z=w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+b$，即$z=w^{T}x+b$。然后，通过激活函数$f(z)$来产生输出。常用的激活函数为单位阶跃函数：$f(z)=\{\begin{array}{ll}1,& z\ge 0\\ 0,& z<0\end{array}$ 。若$f(z)=1$，则样本被分为正类；若$f(z)=0$，则样本被分为负类。

算法过程

• 初始化：随机初始化权重向量$w$和偏置$b$，通常初始值设为较小的随机数。
• 输入与计算：将训练集中的样本$x_i$及其对应的真实标签$y_i$（ y i ∈ { 0 , 1 } y_i \in \{0, 1\} yi​∈{0,1}）输入感知机，计算预测值${\hat{y}}_i=f(w^T{x}_i+b)$ 。
• 更新权重：如果预测值${\hat{y}}_i$与真实标签$y_i$不一致，即预测错误，则更新权重向量$w$和偏置$b$ 。更新公式为：
  $w=w+\eta (y_i-{\hat{y}}_i)x_i$
  $b=b+\eta (y_i-{\hat{y}}_i)$
  其中，$\eta$为学习率，是一个大于0的常数，控制每次更新的步长。学习率通常需要通过试验和调优来确定合适的值。
• 迭代训练：重复上述步骤，对训练集中的所有样本进行多次迭代训练，直到所有样本都能被正确分类，或者达到预设的最大迭代次数。

应用场景

• 文本分类：可用于判断文本的类别，如判断一封邮件是垃圾邮件还是正常邮件，一篇新闻报道属于哪个主题类别等。通过将文本表示为特征向量，利用感知机进行分类决策。
• 图像识别：在简单的图像识别任务中，感知机可用于识别一些具有明显特征的图像，如识别手写数字中的“0”和“1”。将图像中的像素点作为输入特征，经过感知机学习来区分不同的数字。
• 生物信息学：例如在基因序列分析中，感知机可以根据基因的特征来预测其功能或分类，协助生物学家理解基因的作用机制。

优缺点

• 优点：算法简单，易于理解和实现，计算复杂度较低，在处理线性可分的数据时，能够快速收敛并得到分类结果。
• 缺点：只能处理线性可分的数据，对于非线性可分的数据，感知机无法找到一个超平面将不同类别完全分开；学习能力有限，无法解决复杂的分类问题，如异或（XOR）问题；对初始值敏感，不同的初始权重和偏置可能导致最终收敛到不同的结果。

二、神经网络

1.激活函数

激活函数在神经网络中扮演着至关重要的角色，以下从线性模型的局限性、赋予网络非线性能力、引入可学习的非线性变换、增加模型的表达能力、对数据进行特征提取和变换以及实现复杂决策边界等方面，解释为什么神经网络需要激活函数：

1. 克服线性模型的局限性：若神经网络中没有激活函数，那么整个网络将只是一个简单的线性模型。以多层全连接网络为例，假设每一层的权重矩阵为$W_i$，输入为$x$，不考虑偏置时，经过$n$层网络的输出$y=W_n\cdot \cdots \cdot W_2\cdot W_1\cdot x$ ，这本质上还是一个线性变换，其所能表示的关系非常有限。比如在图像识别中，图像中的物体形状、颜色等特征之间的关系往往是非线性的，线性模型无法准确捕捉这些复杂关系，难以实现对图像的有效分类。
2. 赋予网络非线性能力：激活函数能够为神经网络引入非线性因素，使得网络可以学习和模拟各种复杂的非线性关系。例如Sigmoid函数、ReLU函数等，它们具有非线性的函数曲线。以Sigmoid函数$\sigma (z)=\frac{1}{1+e^{-z}}$为例，它将线性输入$z$通过非线性变换映射到$(0,1)$区间内，这样神经网络就能处理非线性问题。如在语音识别任务中，语音信号的特征与识别结果之间存在复杂的非线性关系，激活函数帮助神经网络学习这些关系，从而准确识别语音内容。
3. 引入可学习的非线性变换：激活函数使得神经网络中的每一层都能够对输入数据进行非线性变换，并且这些变换的参数（通过权重和偏置）是可以通过训练学习得到的。不同层的激活函数与权重相结合，能够逐步提取数据中不同层次的特征。例如在卷积神经网络（CNN）中，卷积层之后通常接ReLU激活函数，卷积层负责提取图像的局部特征，ReLU函数则对这些特征进行非线性变换，增强特征的表达能力，使网络能够更好地学习图像的复杂特征。
4. 增加模型的表达能力：神经网络的强大之处在于其能够逼近任意复杂的函数。激活函数是实现这一能力的关键因素之一。理论上，具有足够多隐藏层和神经元，并使用合适激活函数的神经网络可以逼近任何连续函数。例如在回归问题中，如果数据呈现高度非线性分布，使用激活函数的神经网络能够通过调整权重和激活函数的输出，更好地拟合数据，而简单的线性回归模型则难以达到同样的效果。
5. 对数据进行特征提取和变换：激活函数可以对输入数据进行特征提取和变换，将原始数据映射到更有意义的特征空间。例如ReLU函数在处理图像数据时，能够将图像中的一些特征进行增强，抑制一些不重要的特征。当输入为负时，ReLU输出为0，这相当于对数据进行了筛选，保留了具有正响应的特征，有助于提取图像中的边缘、角点等重要特征，提高图像识别的准确率。
6. 实现复杂决策边界：在分类问题中，激活函数帮助神经网络构建复杂的决策边界，从而区分不同类别的数据。例如在多分类任务中，Softmax激活函数（是Sigmoid函数在多分类情况下的推广）将神经网络的输出转换为每个类别的概率分布，使得模型能够根据这些概率做出分类决策，实现复杂的决策边界划分，准确地将数据分到不同类别中。

阶跃函数

sigmoid

Sigmoid函数是一种在机器学习和深度学习领域广泛应用的激活函数。以下从其定义、公式、性质、应用场景等方面为你详细介绍：

定义与公式

Sigmoid函数也称为Logistic函数，它将一个实数输入映射到0到1之间的输出，其数学表达式为：

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

其中，$z$ 是函数的输入，可以是一个标量、向量或矩阵。当 $z$ 为向量或矩阵时，Sigmoid函数对其中每个元素进行上述运算。

性质

1. 值域：函数的值域为 $(0,1)$。这一特性使得Sigmoid函数非常适合用于表示概率，例如在二分类问题中，它可以用来表示样本属于某一类别的概率。
2. 单调性：Sigmoid函数在整个实数域上是单调递增的，其导数恒大于0。这意味着随着输入值 $z$ 的增加，输出值也始终增加，保证了函数在训练过程中的稳定性。
3. 可导性：Sigmoid函数处处可导，其导数可以用自身表示，公式为： ${\sigma }^{\prime }(z)=\sigma (z)(1-\sigma (z))$
   这一性质在基于梯度的优化算法（如反向传播算法）中非常重要，因为它使得计算梯度变得相对简单。
4. 对称性：函数图像关于点 $(0,0.5)$ 中心对称，即 $\sigma (-z)=1-\sigma (z)$ 。

应用场景

1. 二分类问题：在逻辑回归模型中，Sigmoid函数常被用作输出层的激活函数，将模型的预测值转换为属于正类的概率。例如，在判断一封邮件是否为垃圾邮件的任务中，逻辑回归模型通过Sigmoid函数输出邮件为垃圾邮件的概率，然后根据设定的阈值（通常为0.5）进行分类决策。
2. 神经网络隐藏层：在早期的神经网络中，Sigmoid函数也常被用于隐藏层，以引入非线性因素，使神经网络能够学习复杂的非线性关系。然而，由于其存在梯度消失问题，在现代深度神经网络中使用相对较少。
3. 生成对抗网络（GAN）：在GAN的判别器中，Sigmoid函数可用于判断输入数据是真实数据还是生成器生成的假数据，输出值表示输入数据为真实数据的概率。

优缺点

1. 优点
   • 输出范围有限：输出值在 $(0,1)$ 之间，这使得它可以方便地用于表示概率，并且在一些需要将输出限制在特定区间的场景中很有用。
   • 可导性：处处可导的性质为基于梯度的优化算法提供了便利，使得模型能够通过反向传播算法进行训练。
   • 单调性：单调递增的特性有助于模型在训练过程中保持稳定的学习过程。
2. 缺点
   • 梯度消失问题：当输入值的绝对值较大时，Sigmoid函数的导数会趋近于0。在深度神经网络中，这会导致梯度在反向传播过程中逐渐消失，使得网络难以学习到深层的特征。
   • 均值非零：Sigmoid函数的输出均值不为零，这可能导致在神经网络训练过程中，参数更新时出现梯度方向的不一致，从而影响训练效率。
   • 计算复杂度：Sigmoid函数涉及指数运算，相比于一些其他简单的激活函数（如ReLU），计算成本较高。

ReLU函数

ReLU（Rectified Linear Unit）函数，即修正线性单元，是一种在深度学习领域广泛应用的激活函数。以下从其定义、公式、性质、应用场景、优缺点等方面详细介绍：

1. 定义与公式

ReLU函数的定义很简洁，其数学表达式为：
$$ReLU(x)=\{\begin{array}{ll}0,& x<0\\ x,& x\ge 0\end{array}$$

其中 $x$ 为函数的输入，可以是标量、向量或矩阵。当 $x$ 为向量或矩阵时，ReLU函数对其中每个元素进行上述操作。

2. 性质

• 单侧抑制：当输入 $x$ 为负数时，输出为 $0$，起到抑制作用；当输入为正数时，输出等于输入，保留信号。这种特性使得神经网络能够自动学习数据中的重要特征，抑制不重要的信息。
• 稀疏激活：在实际应用中，大量输入数据经过ReLU函数后，会产生很多为 $0$ 的输出，使得激活值变得稀疏。这种稀疏性有助于减少参数之间的相互依赖，提高网络的泛化能力。
• 非线性：ReLU函数是一种非线性函数，它为神经网络引入了非线性因素，使得神经网络能够学习复杂的非线性关系，这是神经网络能够处理各种复杂任务的关键。
• 单调性：在 $x\ge 0$ 的区间上，函数单调递增。单调递增的性质有助于在基于梯度的优化算法中，保持梯度的一致性，使模型训练更加稳定。
• 计算简单：相比于Sigmoid函数等涉及指数运算的激活函数，ReLU函数的计算仅涉及简单的比较和赋值操作，大大降低了计算成本，提高了训练和推理的效率。
• 可导性：在 $x\ne 0$ 的点，函数可导，其导数为：
  $$ReL{U}^{\prime }(x)=\{\begin{array}{ll}0,& x<0\\ 1,& x>0\end{array}$$
  在 $x=0$ 处，导数未定义，但在实际应用中，通常可以将其导数定义为 $0$ 或者 $1$，这对基于梯度的优化算法影响较小，因为在训练过程中，经过该点的情况相对较少。

3. 应用场景

• 卷积神经网络（CNN）：在CNN中，ReLU函数广泛应用于卷积层之后。卷积层负责提取图像的局部特征，ReLU函数对这些特征进行非线性变换，增强特征的表达能力。例如在图像识别任务中，ReLU函数帮助CNN更好地提取图像中的边缘、纹理等重要特征，提高识别准确率。
• 循环神经网络（RNN）及其变体（如LSTM、GRU）：在RNN及其变体中，ReLU函数也常用于隐藏层之间的激活。它能够帮助模型处理序列数据中的非线性关系，例如在自然语言处理任务中，处理文本序列时，ReLU函数有助于模型学习到词语之间的复杂语义关系。
• 多层感知机（MLP）：在传统的MLP中，ReLU函数作为隐藏层的激活函数，使得MLP能够学习复杂的非线性映射，从而在各种分类和回归任务中取得良好的效果。

4. 优缺点

• 优点
  • 有效缓解梯度消失问题：与Sigmoid函数相比，ReLU函数在正数区间的导数恒为 $1$，避免了梯度在反向传播过程中因链式法则不断相乘而导致的梯度消失问题，使得深层神经网络能够有效训练。
  • 计算效率高：由于其计算简单，不涉及复杂的数学运算（如指数运算），在大规模数据的训练和推理过程中，能够显著提高计算速度，减少计算资源的消耗。
  • 收敛速度快：基于ReLU函数的神经网络在训练过程中，通常能够更快地收敛到较好的解，这得益于其简单的计算和良好的梯度特性，使得模型能够更高效地学习数据中的特征。
• 缺点
  • 神经元死亡问题：当输入为负数时，ReLU函数的输出为 $0$，且导数也为 $0$。这意味着在训练过程中，如果某些神经元的输入持续为负，这些神经元将不再更新权重，即发生“神经元死亡”现象，导致该神经元在后续训练中无法恢复。
  • 输出均值不为零：ReLU函数的输出均值不为零，这可能导致在神经网络训练过程中，参数更新时出现梯度方向的不一致，影响训练效率。不过，相比于Sigmoid函数，这种影响相对较小，并且可以通过一些方法（如批量归一化）进行缓解。

2.神经网络矩阵乘法

矩阵乘法示例

在神经网络中，矩阵乘法是实现神经元之间信息传递和计算的核心操作，对于构建和训练神经网络起着关键作用。

基本原理

• 神经元与权重矩阵：神经网络由大量神经元组成，每个神经元接收来自其他神经元的输入信号，并通过特定的计算产生输出。在数学上，神经元的输入可以看作是一个向量，而神经元对这些输入的处理则通过与权重矩阵相乘来实现。假设一个神经元层有 $n$ 个输入神经元和 $m$ 个输出神经元，输入信号可以表示为一个 $n$ 维向量 $\mathbf{x}=[x_1,x_2,\cdots ,x_n{]}^T$，连接这些输入神经元与输出神经元的权重可以组织成一个 $m\times n$ 的矩阵 $\mathbf{W}$，其中每一行对应一个输出神经元与所有输入神经元的连接权重。
• 矩阵乘法运算：输出向量 $\mathbf{y}$ 通过矩阵乘法计算得到，即 $\mathbf{y}=\mathbf{W}\cdot \mathbf{x}$。具体计算过程为：$y_i={\sum }_{j=1}^n{w}_{ij}{x}_j$，其中 $i=1,2,\cdots ,m$，$y_i$ 是输出向量 $\mathbf{y}$ 的第 $i$ 个元素，$w_{ij}$ 是权重矩阵 $\mathbf{W}$ 中第 $i$ 行第 $j$ 列的元素。这一运算过程实际上是对输入信号进行加权求和，每个输入信号的权重由权重矩阵中的对应元素决定。

符号规范

前向传播

3.输出函数

softmax函数

1. 定义与公式

Softmax函数将一个 $K$ 维的实数向量 $\mathbf{z}=[z_1,z_2,\cdots ,z_K]$ 转换为一个 $(0,1)$ 区间内的概率分布向量$\sigma (\mathbf{z})=[\sigma (z_1),\sigma (z_2),\cdots ,\sigma (z_K)]$，其公式为：

$$\sigma (z_j)=\frac{e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}\text{for }j=1,\cdots ,K$$

其中，$z_j$ 是输入向量 $\mathbf{z}$ 的第 $j$ 个元素，$\sigma (z_j)$ 是经过Softmax变换后输出向量的第 $j$ 个元素。

2. 性质

• 概率分布：Softmax函数的输出值总和为 $1$，即 ${\sum }_{j=1}^K\sigma (z_j)=1$，每个输出值都表示对应类别在所有类别中的概率，因此可以将其解释为一个概率分布。
• 单调性：对于输入向量 $\mathbf{z}$ 中的元素 $z_j$，$z_j$ 越大，经过Softmax变换后的 $\sigma (z_j)$ 也越大，并且这种变化是单调的。这意味着Softmax函数能够突出输入向量中较大值对应的类别，抑制较小值对应的类别。
• 可导性：Softmax函数在其定义域内处处可导，这一性质对于基于梯度的优化算法（如随机梯度下降）至关重要，使得在神经网络训练过程中能够通过反向传播算法计算梯度，进而更新模型参数。

3. 应用场景

• 多分类任务：在多分类神经网络中，Softmax函数通常作为输出层的激活函数。例如，在图像分类任务中，模型的最后一层输出一个 $K$ 维向量，其中 $K$ 是类别数，每个元素表示图像属于对应类别的得分。经过Softmax函数处理后，得到的概率分布向量可以直接用于表示图像属于各个类别的概率，然后通过选择概率最大的类别作为预测结果。
• 自然语言处理（NLP）：在NLP的词性标注、命名实体识别等多分类任务中广泛应用。比如在词性标注中，输入一个单词，模型通过Softmax函数输出该单词属于各种词性（如名词、动词、形容词等）的概率，从而确定其词性。

4. 与其他函数对比

• 与Sigmoid函数对比：Sigmoid函数主要用于二分类任务，将一个实数映射到 $(0,1)$ 区间，输出值可解释为正类的概率。而Softmax函数是Sigmoid函数在多分类情况下的推广，适用于多分类问题，将 $K$ 维向量转换为 $K$ 个类别的概率分布。
• 与ReLU函数对比：ReLU函数主要用于神经网络隐藏层，引入非线性因素，以帮助网络学习复杂的非线性关系。而Softmax函数主要用于输出层，将得分转换为概率分布，用于多分类决策。

5. 计算示例

假设输入向量 $\mathbf{z}=[2,1,0.5]$，计算其经过Softmax函数变换后的概率分布：

首先计算分母：

${\sum }_{k=1}^3{e}^{z_k}=e^2+e^1+e^{0.5}\approx 7.389+2.718+1.649=11.756$

然后分别计算每个元素的Softmax值：

$\sigma (z_1)=\frac{e^2}{11.756}\approx \frac{7.389}{11.756}\approx 0.628$

$\sigma (z_2)=\frac{e^1}{11.756}\approx \frac{2.718}{11.756}\approx 0.231$

$\sigma (z_3)=\frac{e^{0.5}}{11.756}\approx \frac{1.649}{11.756}\approx 0.140$

所以经过Softmax变换后的概率分布向量为 $[0.628,0.231,0.140]$。

4.神经网络推理阶段

神经网络的生命周期主要包括训练阶段和推理阶段，推理阶段是在训练好的神经网络基础上进行实际应用的过程，以下为你详细介绍：

定义

神经网络推理阶段指的是，将训练好的神经网络模型应用于新的、未见过的数据，以预测结果或提取有价值信息的过程。 在这个阶段，模型的参数已经固定，不再进行更新，其核心任务是根据输入数据，通过前向传播计算得出输出。

过程

1. 数据预处理：与训练阶段类似，推理阶段的输入数据同样需要进行预处理。这可能包括数据的清洗、归一化、特征提取与转换等操作。例如，在图像识别任务中，输入的图像可能需要调整大小、进行归一化处理，使其符合模型训练时所期望的格式与数据分布。
2. 输入数据：经过预处理的数据被输入到神经网络模型中。这些数据沿着神经网络的层依次向前传播。
3. 前向传播：数据在网络中按照从输入层到隐藏层再到输出层的顺序进行传递。在每一层中，数据会与该层的权重矩阵进行乘法运算，并加上偏置项，然后通过激活函数进行非线性变换（某些层可能不包含激活函数）。例如，在全连接层中，输入向量 $\mathbf{x}$ 与权重矩阵 $\mathbf{W}$ 相乘，再加上偏置向量 $\mathbf{b}$，得到 $\mathbf{y}=\mathbf{Wx}+\mathbf{b}$，随后经过激活函数（如ReLU）得到该层的输出，继续传递到下一层。这个过程不断重复，直到数据到达输出层。
4. 输出结果：在输出层，模型产生最终的输出。输出的形式取决于具体的任务，例如在二分类任务中，输出可能是一个表示属于正类概率的数值；在多分类任务中，输出通常是一个概率分布向量，每个元素代表输入数据属于不同类别的概率，可通过Softmax函数得到；在回归任务中，输出则是一个连续的数值。

与训练阶段的区别

• 模型参数：训练阶段的目标是通过调整模型参数（如权重和偏置），使模型在训练数据上的损失函数最小化，因此参数是不断更新的；而在推理阶段，模型参数已经固定，不再进行更新，直接使用训练好的参数进行计算。
• 计算资源与时间要求：训练阶段通常需要大量的计算资源和较长的时间，因为它要对大量的训练数据进行多次迭代计算，以优化模型参数；推理阶段则更注重实时性，要求在较短的时间内对输入数据给出预测结果，以满足实际应用的需求，如自动驾驶中的实时决策、在线推荐系统的实时响应等。
• 数据特点：训练阶段使用的是大量有标注的训练数据，用于模型的学习和优化；推理阶段处理的是新的、未参与训练的数据，更强调模型对未知数据的泛化能力。

三、神经网络学习

1、神经网络训练的相关概念

训练数据

用来对模型进行训练学习的数据，寻找最优的参数。

测试数据

测试模型的泛化能力的数据。

泛化能力

指模型在训练数据上学习到一些知识后，处理应对未被观察（学习）过的数据的能力。

过拟合

只对某个数据集过度拟合的状态，学习到了数据的个性，忽视了共性。

损失函数

损失函数（Loss Function）在机器学习和深度学习中扮演着核心角色，用于衡量模型预测结果与真实标签之间的差异。以下从其定义、作用、常见类型及选择依据等方面进行介绍：

定义

损失函数是一个非负实值函数，它以模型的预测值和真实值作为输入，输出一个数值来表示两者之间的差异程度。记模型的预测值为 $\hat{y}$，真实值为 $y$，损失函数通常表示为 $L(y,\hat{y})$。

作用

• 指导模型优化：损失函数为模型的训练提供了一个明确的优化目标。在训练过程中，通过调整模型的参数（如神经网络中的权重和偏置），使得损失函数的值最小化。这意味着模型的预测结果越来越接近真实值，从而提高模型的准确性和性能。
• 评估模型性能：它不仅在训练过程中起指导作用，还可以作为评估模型性能的重要指标。在模型训练完成后，通过在验证集或测试集上计算损失函数的值，可以直观地了解模型对数据的拟合程度和泛化能力。损失值越小，通常表示模型的性能越好。

常见类型

• 均方误差损失函数（Mean Squared Error, MSE）
  • 公式：常用于回归任务，计算预测值与真实值之间误差平方的平均值。对于单个样本，其损失为 $L(y,\hat{y})=(y-\hat{y}{)}^2$；对于包含 $n$ 个样本的数据集，均方误差损失函数为 $MSE=\frac{1}{n}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$，其中 $y_i$ 是第 $i$ 个样本的真实值，${\hat{y}}_i$ 是对应的预测值。
  • 特点：对预测值与真实值之间的误差敏感，尤其是较大的误差会被平方放大，这使得模型在训练时更注重减少较大的误差。其函数图像是一个平滑的抛物线，便于使用梯度下降等优化算法进行求解。
• 交叉熵损失函数（Cross - Entropy Loss）
  • 公式：在分类任务中广泛应用。对于二分类问题，常用的是二元交叉熵损失函数，其公式为 $L(y,\hat{y})=-[y\log (\hat{y})+(1-y)\log (1-\hat{y})]$，其中 y ∈ { 0 , 1 } y \in \{0, 1\} y∈{0,1} 是真实标签，$\hat{y}$ 是模型预测为正类的概率。对于多分类问题，使用多分类交叉熵损失函数，假设共有 $C$ 个类别，第 $i$ 个样本的真实类别为 $y_i$（通常用 one - hot 编码表示），模型预测第 $i$ 个样本属于第 $j$ 类的概率为 ${\hat{y}}_{ij}$，则损失函数为 $L=-{\sum }_{i=1}^n{\sum }_{j=1}^C{y}_{ij}\log ({\hat{y}}_{ij})$。
  • 特点：交叉熵损失函数能够很好地反映模型预测概率分布与真实概率分布之间的差异。当模型预测结果越接近真实标签时，损失值越小。在分类问题中，它比均方误差损失函数更能有效指导模型的训练，因为它直接关注预测的类别概率。

选择依据

• 任务类型：回归任务通常选择均方误差损失函数，因为它能直接反映预测值与真实值在数值上的差异；分类任务则多使用交叉熵损失函数或Hinge损失函数，交叉熵损失关注预测概率与真实标签的匹配。
• 模型特点：不同的模型结构可能对损失函数有不同的适应性。例如，神经网络在分类任务中使用交叉熵损失函数往往能取得较好的效果，因为它与神经网络的输出（通常是概率分布）相匹配，且在反向传播过程中计算梯度相对简单。
• 数据特点：如果数据中存在较多噪声或异常值，均方误差损失函数可能会受到较大影响，因为其对误差的平方运算会放大异常值的影响。此时，可以考虑使用对异常值更鲁棒的损失函数，如平均绝对误差损失（Mean Absolute Error, MAE），它与MSE类似，但计算的是误差绝对值的平均值，对异常值的敏感度较低。

2、数值微分

在机器学习中，特别是在基于梯度的优化算法（如梯度下降）中，需要计算损失函数关于模型参数的梯度。对于一些复杂的损失函数，其梯度的解析表达式可能很难推导或计算。此时，数值微分可以作为一种近似计算梯度的方法。虽然数值微分计算梯度的效率相对较低，且可能存在一定的误差（如由于步长 的选择不当导致的截断误差等），但在某些情况下，它为计算梯度提供了一种可行的解决方案，尤其是在对梯度计算的准确性要求不是极高，或者难以通过解析方法得到梯度的情况下。

梯度下降（Gradient Descent）是机器学习和深度学习中广泛使用的优化算法，用于最小化损失函数。学习率（Learning Rate）则是梯度下降算法中的一个重要超参数，它对算法的收敛速度和效果有着关键影响。

梯度下降

1. 基本原理
   梯度下降基于一个简单的数学原理：函数在某点的梯度方向是函数值上升最快的方向，那么其反方向就是函数值下降最快的方向。在机器学习中，我们的目标是最小化损失函数 $L(\theta )$，其中 $\theta$ 是模型的参数（如神经网络中的权重和偏置）。通过不断地沿着损失函数梯度的反方向更新参数，逐步降低损失函数的值，使模型的预测结果更接近真实值。
2. 算法步骤
   • 初始化参数：随机初始化模型的参数 $\theta$。例如，在一个简单的线性回归模型 $y={\theta }_0+{\theta }_{1}x$ 中，随机设定 ${\theta }_0$ 和 ${\theta }_1$ 的初始值。
   • 计算梯度：计算损失函数 $L(\theta )$ 关于参数 $\theta$ 的梯度 ${\nabla }_{\theta }L(\theta )$。例如，对于均方误差损失函数 $L(\theta )=\frac{1}{n}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$（其中 ${\hat{y}}_i$ 是模型的预测值），其关于 $\theta$ 的梯度可以通过求导得到。
   • 更新参数：根据计算得到的梯度，按照以下公式更新参数：
     $$\theta =\theta -\alpha {\nabla }_{\theta }L(\theta )$$
     其中 $\alpha$ 就是学习率，它决定了每次参数更新的步长。
   • 迭代重复：重复上述计算梯度和更新参数的步骤，直到损失函数收敛到一个最小值或者达到预设的最大迭代次数。
3. 梯度下降的类型
   • 批量梯度下降（Batch Gradient Descent, BGD）：在每次更新参数时，使用整个训练数据集来计算梯度。即计算 ${\nabla }_{\theta }L(\theta )=\frac{1}{n}{\sum }_{i=1}^n{\nabla }_{\theta }{L}_i(\theta )$，其中 $L_i(\theta )$ 是第 $i$ 个样本的损失。BGD的优点是每次更新都朝着全局最优解的方向，最终能够收敛到全局最优解（如果损失函数是凸函数）。但缺点是当训练数据量很大时，计算梯度的时间成本非常高，导致训练速度慢。
   • 随机梯度下降（Stochastic Gradient Descent, SGD）：每次更新参数时，只随机选择一个样本 $i$ 来计算梯度，即 ${\nabla }_{\theta }L(\theta )={\nabla }_{\theta }{L}_i(\theta )$。SGD的优点是更新速度快，因为每次只需要计算一个样本的梯度。但由于每次更新的方向是基于单个样本，可能会导致更新方向不稳定，在接近最优解时会在最优解附近波动，难以精确收敛到全局最优解。
   • 小批量梯度下降（Mini - Batch Gradient Descent）：结合了BGD和SGD的优点，每次更新参数时，使用一小部分样本（称为一个小批量，mini - batch）来计算梯度。例如，从训练数据集中随机选择 $m$ 个样本（$m\ll n$），计算 ${\nabla }_{\theta }L(\theta )=\frac{1}{m}{\sum }_{i\in \text{mini - batch}}{\nabla }_{\theta }{L}_i(\theta )$。小批量梯度下降既保证了梯度计算的稳定性，又能利用多个样本的信息，提高了训练速度，是实际应用中最常用的梯度下降类型。

学习率

1. 定义与作用
   学习率 $\alpha$ 是梯度下降算法中的一个超参数，它控制着每次参数更新的步长。学习率的大小直接影响模型的训练效果和收敛速度。
2. 学习率的影响
   • 学习率过大：如果学习率设置得过大，参数更新的步长就会很大，模型可能会在训练过程中跳过最优解，导致无法收敛。在损失函数的图像上表现为，参数更新时会在最优解附近来回跳动，损失函数值不仅不下降，反而可能会上升，甚至出现发散的情况。例如，在一个简单的二次函数 $y=x^2$ 上应用梯度下降算法，如果学习率过大，每次更新 $x$ 的值会过大，从而错过函数的最小值点 $x=0$。
   • 学习率过小：当学习率过小时，参数更新的步长很小，模型的收敛速度会非常缓慢。虽然最终可能会收敛到最优解，但需要花费大量的时间和计算资源进行多次迭代。这就好比在一个很长的斜坡上，每次只走一小步，到达坡底（最优解）需要很长时间。
3. 学习率的调整策略
   • 固定学习率：在训练过程中，学习率始终保持不变。这种方法简单直观，但可能无法兼顾模型在不同训练阶段对学习率的需求。
   • 动态学习率：
     • 学习率衰减（Learning Rate Decay）：随着训练的进行，逐渐减小学习率。常见的方法有指数衰减（${\alpha }_t={\alpha }_0\cdot {\gamma }^t$，其中 ${\alpha }_t$ 是第 $t$ 次迭代时的学习率，${\alpha }_0$ 是初始学习率，$\gamma$ 是衰减因子，$0<\gamma <1$）、步长衰减（每经过一定的迭代次数，将学习率乘以一个固定的衰减因子）等。在训练初期，较大的学习率可以加快模型的收敛速度；随着训练的推进，减小学习率可以使模型更精确地逼近最优解。
     • 自适应学习率：一些优化算法（如Adagrad、Adadelta、RMSProp、Adam等）能够根据参数的更新情况自适应地调整学习率。例如，Adagrad算法为每个参数分配一个学习率，对经常更新的参数使用较小的学习率，对不经常更新的参数使用较大的学习率，从而在不同参数上实现更灵活的学习率调整。

3、神经网络学习步骤

神经网络的学习过程是一个复杂且系统的过程，旨在通过不断调整网络的参数，使得模型能够准确地对输入数据进行预测或分类。下面将详细介绍神经网络学习的主要步骤：

1. 数据准备

• 数据收集：根据具体的任务需求，收集相关的数据。例如，在图像分类任务中，需要收集包含各种类别图像的数据集；在自然语言处理任务中，可能需要收集文本数据。数据的来源可以是公开数据集、实际业务系统或者通过爬虫等方式获取。
• 数据清洗：对收集到的数据进行清洗，去除其中的噪声、重复数据、错误数据等。例如，在图像数据中，可能存在模糊不清、损坏的图像；在文本数据中，可能存在拼写错误、乱码等问题，都需要进行处理。
• 数据划分：将清洗后的数据划分为训练集、验证集和测试集。训练集用于模型的训练，验证集用于在训练过程中评估模型的性能，调整超参数，防止过拟合。测试集则用于在模型训练完成后，对模型的最终性能进行评估。常见的划分比例为训练集占 70% - 80%，验证集占 10% - 15%，测试集占 10% - 15%。
• 数据预处理：对数据进行预处理，使其适合神经网络的输入。对于图像数据，可能需要进行归一化、缩放、裁剪、旋转等操作；对于文本数据，需要进行分词、词嵌入等处理。

2. 模型设计

• 确定网络结构：根据任务的复杂度和数据的特点，确定神经网络的结构，包括层数、每层的神经元数量、连接方式等。例如，对于简单的分类任务，可以使用多层感知机（MLP）；对于图像任务，通常使用卷积神经网络（CNN）；对于序列数据，如文本和时间序列，循环神经网络（RNN）及其变体（如 LSTM、GRU）更为合适。
• 选择激活函数：在神经网络的隐藏层和输出层选择合适的激活函数，为网络引入非线性因素，使其能够学习复杂的非线性关系。常见的激活函数有 ReLU、Sigmoid、Tanh 等。在输出层，对于二分类任务通常使用 Sigmoid 函数，对于多分类任务使用 Softmax 函数。
• 初始化参数：随机初始化神经网络的权重和偏置。合适的初始化方法可以加速模型的收敛，避免梯度消失或梯度爆炸问题。常见的初始化方法有随机初始化、 Xavier 初始化、He 初始化等。

3. 定义损失函数

• 选择损失函数：根据具体的任务类型，选择合适的损失函数来衡量模型预测结果与真实标签之间的差异。对于回归任务，常用的损失函数是均方误差（MSE）；对于分类任务，常用的是交叉熵损失函数。
• 损失函数的作用：损失函数为模型的训练提供了一个明确的优化目标，通过不断调整模型的参数，使得损失函数的值最小化，从而提高模型的性能。

4. 选择优化算法

• 常见优化算法：选择合适的优化算法来更新神经网络的参数，使得损失函数最小化。常见的优化算法有梯度下降（GD）、随机梯度下降（SGD）、小批量梯度下降（Mini - Batch GD）以及一些自适应优化算法，如 Adagrad、Adadelta、RMSProp、Adam 等。
• 优化算法的作用：优化算法通过计算损失函数关于参数的梯度，确定参数更新的方向和步长，使得模型能够朝着损失函数减小的方向不断调整参数。

5. 模型训练

• 前向传播：将训练集中的样本输入到神经网络中，数据从输入层经过隐藏层，最终传递到输出层，得到模型的预测结果。在每一层中，数据与该层的权重矩阵相乘，加上偏置，然后通过激活函数进行非线性变换。
• 计算损失：根据模型的预测结果和真实标签，使用定义好的损失函数计算损失值。损失值反映了模型在当前参数下的预测误差。
• 反向传播：根据计算得到的损失值，使用链式法则计算损失函数关于每个参数的梯度。反向传播从输出层开始，逐层计算梯度，将梯度信息传递回每一层的参数。
• 参数更新：使用选择的优化算法，根据计算得到的梯度更新神经网络的参数。例如，在梯度下降算法中，参数更新公式为 $\theta =\theta -\alpha {\nabla }_{\theta }L$，其中 $\theta$ 是参数，$\alpha$ 是学习率，${\nabla }_{\theta }L$ 是损失函数关于参数的梯度。
• 迭代训练：重复上述前向传播、计算损失、反向传播和参数更新的步骤，对训练集进行多次迭代训练，直到损失函数收敛或达到预设的最大迭代次数。

6. 模型评估

• 使用验证集评估：在训练过程中，定期使用验证集对模型的性能进行评估。计算验证集上的损失值和其他评估指标（如准确率、召回率、F1 值等），观察模型在验证集上的性能变化，判断模型是否过拟合或欠拟合。
• 调整超参数：根据验证集的评估结果，调整模型的超参数，如学习率、批量大小、网络层数、神经元数量等。超参数的调整可以通过手动调整、网格搜索、随机搜索等方法进行。

7. 模型测试

• 使用测试集评估：在模型训练和超参数调整完成后，使用测试集对模型的最终性能进行评估。测试集的数据在训练过程中未被使用过，因此可以更客观地评估模型的泛化能力。
• 分析评估结果：分析模型在测试集上的评估结果，判断模型是否满足实际应用的需求。如果模型的性能不理想，可以考虑重新调整模型结构、收集更多数据或尝试其他方法。

8. 模型部署

• 模型保存：将训练好的模型保存下来，以便后续使用。保存的内容通常包括模型的结构和参数。
• 模型部署：将保存的模型部署到实际应用环境中，如服务器、移动设备等。在部署过程中，需要考虑模型的性能、资源占用、兼容性等问题。

四、误差反向传播

误差反向传播（Backpropagation，简称BP）算法是训练神经网络的核心算法，它基于梯度下降的思想，通过计算损失函数关于网络参数的梯度来更新参数，使得损失函数值不断减小。以下详细介绍误差反向传播的过程：

1. 前向传播计算预测值

假设神经网络有输入层、若干隐藏层和输出层。给定输入样本 $x$，数据从输入层开始，按照网络结构依次经过各层的计算，最终得到输出层的预测值 $\hat{y}$。

• 隐藏层计算：对于隐藏层 $l$，其输入为前一层 $l-1$ 的输出 $a^{l-1}$。首先进行线性变换，计算 $z^l=W^l{a}^{l-1}+b^l$，其中 $W^l$ 是第 $l$ 层的权重矩阵，$b^l$ 是偏置向量。然后通过激活函数 $\sigma$ 进行非线性变换，得到该层的输出 $a^l=\sigma (z^l)$。

• 输出层计算：输出层的计算过程与隐藏层类似，只是可能使用特定的激活函数以适应任务需求。例如，对于二分类任务，输出层可能使用 Sigmoid 函数；对于多分类任务，通常使用 Softmax 函数。假设输出层为第 $L$ 层，经过线性变换 $z^L=W^L{a}^{L-1}+b^L$ 后，通过相应激活函数得到预测值 $\hat{y}=\sigma (z^L)$。

2. 计算损失函数

根据预测值 $\hat{y}$ 和真实标签 $y$，选择合适的损失函数 $L(y,\hat{y})$ 来衡量预测值与真实值之间的差异。常见的损失函数有均方误差损失（用于回归任务）、交叉熵损失（用于分类任务）等。

例如，对于均方误差损失函数，其定义为 $L(y,\hat{y})=\frac{1}{2}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$，其中 $n$ 是样本数量，$y_i$ 和 ${\hat{y}}_i$ 分别是第 $i$ 个样本的真实值和预测值。

3. 反向传播计算梯度

从输出层开始，反向计算损失函数关于各层参数（权重 $W$ 和偏置 $b$）以及各层输入 $z$ 的梯度。

• 输出层梯度计算：

  • 计算损失函数关于输出层线性组合 $z^L$ 的梯度 ${\delta }^L$。以均方误差损失函数和 Sigmoid 激活函数为例，首先对损失函数求关于 $\hat{y}$ 的导数 $\frac{\partial L}{\partial \hat{y}}=(\hat{y}-y)$，然后根据链式法则，${\delta }^L=\frac{\partial L}{\partial \hat{y}}\cdot {\sigma }^{\prime }(z^L)$，其中 ${\sigma }^{\prime }(z^L)$ 是 Sigmoid 函数在 $z^L$ 处的导数。
  • 计算损失函数关于输出层权重 $W^L$ 和偏置 $b^L$ 的梯度。
    • $\frac{\partial L}{\partial W^L}={\delta }^L(a^{L-1}{)}^T$
    • $\frac{\partial L}{\partial b^L}={\delta }^L$

• 隐藏层梯度计算：对于隐藏层 $l$（$1<l<L$），从后往前依次计算：

  • 计算该层的误差项 ${\delta }^l$。根据链式法则，${\delta }^l=((W^{l+1}{)}^T{\delta }^{l+1})\cdot {\sigma }^{\prime }(z^l)$，其中 $(W^{l+1}{)}^T{\delta }^{l+1}$ 表示将下一层的误差项传递到当前层，${\sigma }^{\prime }(z^l)$ 是当前层激活函数在 $z^l$ 处的导数。
  • 计算损失函数关于当前层权重 $W^l$ 和偏置 $b^l$ 的梯度。
    • $\frac{\partial L}{\partial W^l}={\delta }^l(a^{l-1}{)}^T$
    • $\frac{\partial L}{\partial b^l}={\delta }^l$

4. 参数更新

根据计算得到的梯度，使用优化算法（如梯度下降算法）更新神经网络的参数。

以梯度下降算法为例，更新公式如下：

• 权重更新：$W^l:=W^l-\alpha \frac{\partial L}{\partial W^l}$
• 偏置更新：$b^l:=b^l-\alpha \frac{\partial L}{\partial b^l}$

其中 $\alpha$ 是学习率，控制每次参数更新的步长。

通过不断重复上述前向传播、计算损失、反向传播计算梯度和参数更新的过程，神经网络的参数逐渐调整，使得损失函数值不断减小，模型的预测性能逐步提升。

五、与学习相关的技巧

1、优化器的选取（下降方法）

a. SGD

• 原理：SGD每次从训练数据集中随机选择一个样本，计算该样本的损失函数关于模型参数的梯度，并根据梯度更新参数。与批量梯度下降（BGD）每次使用全部训练数据计算梯度不同，SGD的更新方向仅基于单个样本的梯度，这使得它的更新速度更快，尤其是在大规模数据集上。

• 优点：计算效率高，每次只需要计算一个样本的梯度，内存需求小，适用于大规模数据集。能够在一定程度上避免陷入局部最优解，因为每次更新的方向具有一定随机性。

• 缺点：由于每次更新仅基于一个样本的梯度，其更新方向可能波动较大，导致模型收敛过程不稳定。在接近最优解时，可能会在最优解附近来回振荡，难以精确收敛到全局最优解。

b. Momentum

• 原理：Momentum在SGD的基础上引入了动量的概念，它会积累之前梯度的信息，使得参数更新方向不仅取决于当前样本的梯度，还与之前的梯度方向有关。这就如同物体在运动过程中具有惯性，会沿着之前的运动方向继续前进，从而减少更新过程中的波动，加快收敛速度。
• 优点：能够加速模型收敛，特别是在梯度方向一致的情况下，可以快速沿着该方向前进。减少了梯度更新的波动，使得参数更新更加稳定，有助于避免在局部最优解附近振荡。
• 缺点：如果初始学习率设置过大，可能会导致模型在训练过程中错过最优解，因为动量会使参数更新在错误的方向上持续一段时间。

c. AdaGrad

• 原理：AdaGrad为每个参数自适应地调整学习率。它根据每个参数在以往迭代过程中的梯度累积情况，动态地调整学习率。对于经常更新的参数，由于其梯度累积较大，会降低其学习率；而对于不经常更新的参数，则会提高其学习率。
• 优点：无需手动调整学习率，算法能够自动为每个参数分配合适的学习率，这在处理高维数据或数据稀疏的情况下非常有效。对于不同的参数，能够根据其更新频率自适应地调整学习率，提高了模型的收敛速度和稳定性。
• 缺点：由于累积梯度平方会不断累加，导致分母不断增大，使得学习率在训练后期变得非常小，可能导致模型过早收敛到次优解，无法进一步优化

d. Adam

• 原理：Adam结合了Momentum和RMSProp（均方根传播，一种类似AdaGrad的算法）的优点，既考虑了梯度的一阶矩（均值），又考虑了梯度的二阶矩（未中心化的方差）。通过对梯度的一阶矩和二阶矩进行估计，并利用这些估计值自适应地调整每个参数的学习率。
• 优点：自适应调整学习率，在不同参数上能够根据其梯度的统计特性进行灵活调整，通常不需要过多手动调参。结合了Momentum和RMSProp的优点，既能够加速收敛，又能在训练后期保持较好的稳定性，在许多深度学习任务中表现出色。
• 缺点：在某些情况下，可能会出现过度适应的问题，导致模型在训练后期收敛速度变慢。此外，Adam算法对超参数 ${\beta }_1$ 和 ${\beta }_2$ 的选择较为敏感，如果设置不当，可能会影响模型的性能。

e.AdamW

AdamW是对Adam优化算法的改进，它结合了Adam的自适应学习率特性和权重衰减（L2正则化）的优势，旨在更有效地训练深度学习模型，防止过拟合。下面从其原理、与Adam的对比、优势、应用场景等方面详细介绍：

与Adam的对比

• 正则化方式：Adam通常是在损失函数中加入L2正则化项来实现权重衰减；而AdamW直接在参数更新步骤中应用权重衰减，这种分离的方式使得权重衰减的效果更加清晰和可控。
• 正则化效果：在Adam中，由于正则化项的梯度与梯度的二阶矩估计相互影响，可能会导致权重衰减的效果不稳定。而AdamW避免了这种干扰，能够更有效地控制模型的复杂度，防止过拟合。

优势

• 更好的正则化效果：AdamW能够更有效地对模型参数进行正则化，减少过拟合的风险。在处理大规模数据集和复杂模型时，它可以帮助模型学习到更泛化的特征，提高模型在测试集上的性能。
• 适应性强：继承了Adam算法自适应学习率的优点，能够根据不同参数的梯度特性自动调整学习率，使得模型在训练过程中能够更快地收敛。同时，权重衰减的加入进一步增强了模型的稳定性和泛化能力。

应用场景

• 深度学习模型训练：AdamW广泛应用于各种深度学习任务，如计算机视觉（如图像分类、目标检测、语义分割）、自然语言处理（如文本分类、机器翻译、情感分析）等。在这些任务中，模型通常具有大量的参数，容易出现过拟合问题，AdamW可以有效地缓解这一问题。
• 预训练模型微调：在微调预训练模型时，AdamW也表现出色。预训练模型已经在大规模数据上进行了训练，具有一定的泛化能力，但在微调过程中，由于数据分布的变化和模型结构的调整，仍然可能出现过拟合。AdamW的权重衰减机制可以帮助模型更好地适应新的数据，保持良好的泛化性能。

2、批归一化

原理

在深度神经网络的训练过程中，随着网络层数的增加，参数更新会导致各层输入数据的分布不断变化，这种现象被称为“内部协变量偏移”（Internal Covariate Shift）。这会使得模型的训练变得困难，需要使用较低的学习率并花费更多的时间来收敛。批归一化通过对每一层的输入进行归一化处理，将其重新拉回到均值为0、方差为1的标准正态分布，从而缓解内部协变量偏移问题。

具体来说，对于神经网络某一层的输入 $x$，批归一化不是对单个样本进行操作，而是对一个mini - batch的数据进行处理。假设一个mini - batch的数据为 B = { x 1 , x 2 , . . . , x m } B = \{x_1, x_2,..., x_m\} B={x1​,x2​,...,xm​}，其中 $m$ 是mini - batch的大小。

算法步骤

1. 标准化：首先计算mini - batch数据的均值 ${\mu }_B$ 和方差 ${\sigma }_B^2$：
   ${\mu }_B=\frac{1}{m}{\sum }_{i=1}^m{x}_i$
   ${\sigma }_B^2=\frac{1}{m}{\sum }_{i=1}^m(x_i-{\mu }_B{)}^2$
   然后对每个样本 $x_i$ 进行标准化：
   ${\hat{x}}_i=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$
   其中 $ϵ$ 是一个很小的常数（如 $1e-5$），用于防止分母为零。

2. 缩放与平移：经过标准化后的 ${\hat{x}}_i$ 虽然均值为0，方差为1，但这样可能会限制模型的表达能力。因此，批归一化引入了两个可学习的参数 $\gamma$ 和 $\beta$，对标准化后的数据进行缩放和平移：
   $y_i=\gamma {\hat{x}}_i+\beta$
   $\gamma$ 和 $\beta$ 是与 $x_i$ 同维度的向量，在训练过程中通过反向传播算法进行学习。

作用

1. 加速训练：批归一化使得每层的输入数据分布相对稳定，这样可以使用较大的学习率，加快模型的收敛速度。实验表明，使用批归一化后，模型的训练时间可以显著缩短。
2. 提高模型稳定性：减少了内部协变量偏移，使得模型对参数初始化和超参数的选择不再那么敏感，降低了模型训练过程中梯度消失或梯度爆炸的风险，提高了模型训练的稳定性。
3. 正则化效果：在一定程度上起到了正则化的作用。由于批归一化在训练过程中使用mini - batch的数据进行归一化，每个mini - batch的均值和方差都在变化，这类似于在数据中引入了噪声，从而增加了模型的泛化能力。

3、正则化

过拟合

• 定义：过拟合是指模型在训练数据上表现出非常高的准确性，但在新的、未见过的数据（测试数据）上表现很差的现象。此时，模型过度学习了训练数据中的细节和噪声，包括一些特定于训练数据的偶然特征，而没有捕捉到数据的通用模式，导致模型的泛化能力下降。
• 原因：
  • 模型复杂度高：当模型具有过多的参数或复杂的结构时，它有足够的能力去拟合训练数据中的每一个细节，包括噪声，从而导致过拟合。
  • 训练数据量不足：如果训练数据量较少，模型没有足够的数据来学习到数据的通用特征，就容易过度依赖训练数据中的个别特征，从而导致过拟合。例如，在图像分类任务中，如果只有少量的图像用于训练，模型可能会记住这些图像的特定细节，而无法对其他图像进行准确分类。
• 影响：过拟合使得模型在实际应用中失去可靠性，因为它不能准确地对新数据进行预测或分类，无法满足实际需求。

正则化

• 定义：正则化是一类通过限制模型复杂度，防止过拟合，提高模型泛化能力的方法。其核心思想是在损失函数中加入一个正则化项，对模型的参数进行约束，使得模型不能随意地拟合训练数据中的噪声和细节。
• 作用：通过对模型参数进行约束，正则化可以防止模型过于复杂，迫使模型学习到更具普遍性的特征，从而在训练数据和测试数据上都能保持较好的性能。
• 常见类型：
  • L1正则化：在损失函数中添加L1正则化项，即参数的绝对值之和乘以一个正则化系数 $\lambda$。对于线性回归模型，损失函数 $L=\frac{1}{n}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2+\lambda {\sum }_{j=0}^p|{\theta }_j|$，其中 $n$ 是样本数量，$y_i$ 是真实值，${\hat{y}}_i$ 是预测值，${\theta }_j$ 是模型参数，$p$ 是参数的数量。L1正则化倾向于使部分参数变为0，从而实现特征选择，减少模型的复杂度。
  • L2正则化：在损失函数中添加L2正则化项，即参数的平方和乘以一个正则化系数 $\lambda$。对于线性回归模型，损失函数 $L=\frac{1}{n}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2+\frac{\lambda }{2}{\sum }_{j=0}^p{\theta }_j^2$。L2正则化使得参数的值趋于较小但不为0，它通过对参数的缩放来限制模型的复杂度。

权值衰减（L2正则化的一种解释）

• 定义：权值衰减通常指的就是L2正则化。在梯度下降等优化算法中，每次更新参数时，除了根据损失函数的梯度进行更新外，还会对参数进行一个与参数值本身成正比的衰减操作。以线性回归模型的梯度下降更新公式为例，对于参数 ${\theta }_j$，更新公式为 ${\theta }_j:={\theta }_j-\alpha \left(\frac{\partial L}{\partial {\theta }_j}+\lambda {\theta }_j\right)$，其中 $\alpha$ 是学习率，$\frac{\partial L}{\partial {\theta }_j}$ 是损失函数关于参数 ${\theta }_j$ 的梯度，$\lambda {\theta }_j$ 就是权值衰减项。
• 原理：权值衰减通过在每次参数更新时，将参数值向0的方向进行一定程度的收缩，使得参数不会变得过大。较大的参数值可能会导致模型对训练数据的过度拟合，而权值衰减限制了参数的增长，从而防止过拟合。直观上，它使得模型更倾向于使用多个较小的权重，而不是少数几个较大的权重，这有助于模型学习到更平滑的函数，提高泛化能力。

Dropout

• 定义：Dropout是一种在神经网络训练过程中随机丢弃神经元的正则化方法。在训练过程中，对于神经网络的每一层，以一定的概率 $p$ 随机地将该层中的神经元及其连接暂时从网络中丢弃，即这些神经元在本次前向传播和反向传播中不参与计算。这样，每次迭代时，网络的结构都是不同的，相当于训练了多个不同的子网络。
• 原理：Dropout通过随机丢弃神经元，打破了神经元之间的协同适应性。在没有Dropout的情况下，神经元之间可能会相互依赖，共同适应训练数据中的噪声和特定模式。而Dropout使得每个神经元都不能依赖于其他特定的神经元，从而迫使模型学习到更鲁棒的特征表示，提高模型的泛化能力。
• 优点：
  • 计算简单：实现Dropout非常简单，只需要在训练过程中随机丢弃神经元，不需要额外的复杂计算。
  • 有效防止过拟合：在许多深度学习任务中，Dropout能够显著提高模型的泛化能力，减少过拟合现象。
  • 减少参数调整：相比于其他正则化方法，Dropout对超参数的调整相对不那么敏感，通常只需要调整丢弃概率 $p$，一般在0.2 - 0.5之间。
• 缺点：
  • 训练时间增加：由于每次迭代中网络结构都在变化，训练时间通常会比不使用Dropout时有所增加。
  • 推理时的不确定性：在推理时，为了得到合理的输出，需要将所有神经元的输出乘以训练时的保留概率 $1-p$，这在一定程度上增加了推理的复杂性和不确定性。

六、卷积神经网络

1、卷积层

卷积神经网络（Convolutional Neural Network，缩写CNN）是一种专门为处理具有网格结构数据（如图像、音频）而设计的深度学习模型，在计算机视觉、语音识别等众多领域取得了卓越成就。以下从其结构组成、工作原理、优势及应用场景等方面进行介绍。

结构组成

1. 卷积层：
   • 核心操作：卷积层是CNN的核心组件，通过卷积核在输入数据上滑动进行卷积操作。卷积核是一个可学习的小矩阵，它在输入数据的局部区域上进行元素对应相乘并求和，从而生成特征图。 例如，对于一个二维图像，卷积核在图像上逐像素滑动，每次计算一个局部区域与卷积核的卷积结果，得到特征图上的一个像素值。
   • 特征提取：不同的卷积核可以提取不同的特征，如边缘检测卷积核可以突出图像中的边缘信息，纹理卷积核可以捕捉图像的纹理特征。随着卷积层的堆叠，网络可以从低级特征（如边缘、角点）逐渐学习到高级抽象特征（如物体的部分、整体形状）。
2. 池化层：
   • 操作方式：池化层主要用于对特征图进行下采样，常见的池化方式有最大池化和平均池化。 最大池化是在一个局部区域内选取最大值作为输出，平均池化则是计算局部区域内的平均值作为输出。例如，在一个 $2\times 2$ 的窗口上进行最大池化，窗口在特征图上滑动，每次取窗口内的最大值作为池化后的输出值。
   • 作用：池化层可以减少数据的维度，降低计算量，同时保留主要特征。 它在一定程度上还能增强模型对输入数据的平移不变性，即输入数据在小范围内的平移不会影响池化后的结果。
3. 全连接层：
   • 连接方式：全连接层中每个神经元都与上一层的所有神经元相连，将经过卷积层和池化层提取的特征进行整合，映射到最终的类别空间或回归目标。例如，在图像分类任务中，全连接层将提取到的图像特征转换为各类别的概率值。
   • 功能：全连接层在模型中起到分类或回归的决策作用，它根据前面层提取的特征进行综合判断，输出最终的预测结果。
4. 激活函数层：
   • 常用函数：在卷积层和全连接层之后通常会使用激活函数，为模型引入非线性因素。常见的激活函数有ReLU（Rectified Linear Unit）、Sigmoid、Tanh等。其中，ReLU因其计算简单、能够有效缓解梯度消失问题而被广泛应用，其公式为 $$f(x)=\{\begin{array}{ll}x,& x\ge 0\\ 0,& x<0\end{array}$$
   • 作用：如果没有激活函数，CNN将只是一个线性模型，只能学习线性关系。激活函数使模型能够学习到复杂的非线性关系，大大增强了模型的表达能力。

工作原理

1. 前向传播：
   • 输入数据（如图像）首先进入卷积层，通过卷积核的卷积操作提取特征，生成特征图。
   • 特征图经过激活函数进行非线性变换，然后进入池化层进行下采样，减少数据维度。
   • 经过多次卷积、激活和池化操作后，数据进入全连接层，最终输出预测结果。 例如在图像分类任务中，输出为图像属于各个类别的概率。
2. 反向传播：在训练过程中，计算预测结果与真实标签之间的损失函数（如交叉熵损失用于分类任务，均方误差损失用于回归任务）。然后，通过反向传播算法，从输出层开始，将损失函数关于各层参数（卷积核权重、全连接层权重等）的梯度反向传播回前面的层，根据梯度更新参数，使得损失函数逐渐减小。这个过程不断迭代，直到模型收敛。

优势

1. 局部感知：卷积核在局部区域上进行卷积操作，使得网络能够捕捉数据的局部特征，符合图像等数据的局部相关性特点。例如，图像中的物体通常由局部的边缘、纹理等特征组成，卷积层可以有效地提取这些局部信息。
2. 参数共享：同一个卷积核在输入数据的不同位置上滑动使用，共享相同的参数。这大大减少了模型的参数数量，降低计算量，同时提高了模型的泛化能力。例如，一个用于边缘检测的卷积核可以在图像的不同位置检测边缘，而不需要为每个位置都学习一组不同的参数。
3. 平移不变性：池化层的操作使得模型对输入数据的平移具有一定的不变性。即使图像中的物体在位置上有小的变化，经过池化后提取的特征仍然相似，从而提高了模型的鲁棒性。

4、具有代表性的CNN

1、LeNet

• 提出时间与背景：由Yann LeCun等人在1998年提出，是最早成功应用于数字识别任务的卷积神经网络之一，为后续CNN的发展奠定了基础。
• 网络结构：
  • 输入层：通常接收大小为 $32\times 32$ 的图像。
  • 卷积层：包含多个卷积层，如C1层使用 $6$ 个 $5\times 5$ 的卷积核，生成 $6$ 个特征图；C3层使用 $16$ 个不同大小的卷积核，进一步提取特征。
  • 池化层：采用平均池化，例如S2层对C1层的输出进行 $2\times 2$ 的平均池化，降低数据维度。
  • 全连接层：包含多个全连接层，如F5、F6层，将前面提取的特征进行整合，最终输出分类结果。
  • 输出层：使用Softmax函数输出数字0 - 9的概率分布。
• 特点与贡献：
  • 首次展示了CNN在图像识别任务中的有效性，证明了卷积、池化等操作在特征提取和降维方面的作用。
  • 其网络结构为后续CNN的设计提供了重要的参考范式，许多现代CNN架构都借鉴了LeNet的基本组成部分。

2、AlexNet

• 提出时间与背景：在2012年由Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton提出，在当年的ImageNet大规模视觉识别挑战赛（ILSVRC）中取得了显著的成绩，推动了深度学习的复兴。
• 网络结构：
  • 输入层：接收 $224\times 224\times 3$ 的彩色图像。
  • 卷积层：包含多个卷积层，如使用 $11\times 11$、$5\times 5$ 和 $3\times 3$ 等不同大小的卷积核，通过卷积操作提取图像特征。
  • 池化层：采用最大池化，例如在一些卷积层后使用 $3\times 3$ 步长为2的最大池化，降低数据维度。
  • 全连接层：有多个全连接层，将卷积层提取的特征进行综合处理，最终输出分类结果。
  • 输出层：使用Softmax函数进行分类。此外，还引入了Dropout层，随机丢弃神经元，防止过拟合。
• 特点与贡献：
  • 证明了深度CNN在大规模图像数据集上的强大性能，展示了GPU加速训练的可行性，为深度学习在计算机视觉领域的广泛应用奠定了基础。
  • 引入ReLU激活函数，解决了Sigmoid等函数存在的梯度消失问题，加速了网络的收敛。同时，Dropout技术的应用有效减轻了过拟合现象。

3、VGG

• 提出时间与背景：由牛津大学视觉几何组（Visual Geometry Group）的Karen Simonyan和Andrew Zisserman在2014年提出，在ILSVRC 2014比赛中获得定位任务第一名和分类任务第二名。
• 网络结构：
  • 输入层：通常接收 $224\times 224\times 3$ 的图像。
  • 卷积层：VGG的显著特点是使用了多个连续的 $3\times 3$ 小卷积核进行卷积操作，通过堆叠这些小卷积核来增加网络深度。例如，VGG16包含13个卷积层，VGG19包含16个卷积层。多个 $3\times 3$ 卷积层的组合在感受野上等效于一个大的卷积核，但参数数量更少，且能增加网络的非线性。
  • 池化层：使用 $2\times 2$ 的最大池化，在卷积层之间进行下采样。
  • 全连接层：与AlexNet类似，包含3个全连接层，用于最终的分类。
  • 输出层：使用Softmax函数输出分类结果。
• 特点与贡献：
  • 证明了增加网络深度可以有效提升模型性能，为深度神经网络的发展提供了重要的思路。其简洁且规整的网络结构易于实现和理解，成为后续许多网络结构设计的基础。
  • $3\times 3$ 小卷积核的使用模式在提高模型性能的同时，减少了参数数量，提高了计算效率。

4、GoogleNet

• 提出时间与背景：由谷歌的Christian Szegedy等人在2014年提出，同样在ILSVRC 2014比赛中表现出色，获得分类任务第一名。
• 网络结构：
  • 输入层：接收 $224\times 224\times 3$ 的图像。
  • Inception模块：这是GoogleNet的核心组件，它通过不同大小的卷积核（如 $1\times 1$、$3\times 3$、$5\times 5$）和池化操作并行处理输入，然后将这些结果拼接在一起，从而在不同尺度上提取特征。这种结构可以有效增加网络的宽度和对特征的适应性。
  • 辅助分类器：在网络中间层引入了两个辅助分类器，将中间层的特征用于分类任务，并将分类损失以一定权重加到总损失中。这有助于解决梯度消失问题，同时加强了对中间层特征的学习。
  • 输出层：使用Softmax函数输出分类结果。
• 特点与贡献：
  • Inception模块的设计是一种创新的网络架构设计思路，通过多尺度特征融合，在增加网络表达能力的同时控制了计算量。
  • 辅助分类器的引入为训练深度网络提供了一种有效的手段，有助于网络的收敛和性能提升。

5、ResNet

• 提出时间与背景：由微软亚洲研究院的何恺明等人在2015年提出，解决了深度神经网络训练过程中的梯度消失和梯度爆炸问题，使得训练非常深的网络成为可能。
• 网络结构：
  • 输入层：接收图像数据，常见的输入尺寸为 $224\times 224\times 3$。
  • 残差块：这是ResNet的核心结构。传统神经网络在加深网络层数时，会出现性能下降的问题。而残差块通过引入跳跃连接（shortcut connection），使得网络可以学习残差映射 $F(x)=H(x)-x$，其中 $H(x)$ 是期望学习的映射，$x$ 是输入。这样，网络只需要学习输入与输出之间的差异，而不是直接学习复杂的映射 $H(x)$，大大简化了学习过程。
  • 输出层：经过多个残差块堆叠后，通过全连接层和Softmax函数输出分类结果。
• 特点与贡献：
  • 残差网络结构突破了深度神经网络训练的瓶颈，使得网络深度可以大幅增加，从而提升模型的性能。例如，ResNet-50、ResNet-101和ResNet-152等不同深度的模型在各种计算机视觉任务中都取得了优异的成绩。
  • 为后续深度神经网络的发展提供了重要的基础，许多先进的网络结构都基于ResNet进行改进和扩展。

七、自然语言和单词的分布式表示

1、自然语言处理

我们平常使用的语言，如日语或英语，称为自然语言（natural language）。所谓自然语言处理（Natural Language Processing，NLP），顾名思义，就是处理自然语言的科学。

三种方法

1. 基于同义词词典的方法
2. 基于计数的方法
3. 基于推理的方法（word2vec）

2、基于同义词词典的方法

• 原理：利用预先构建好的同义词词典，如《同义词词林》等，来获取词汇之间的语义关系。这些词典通常按照一定的语义类别对词汇进行分类，将具有相似意义的词归为一组。例如，在同义词词典中，“美丽”“漂亮”“好看”等词可能会被归为同一类，表示相近的语义。
• 应用场景：
  • 文本相似度计算：通过查找两个文本中词汇在同义词词典中的对应关系，判断它们的语义相似程度。比如，要比较“这朵花很美丽”和“这朵花真漂亮”，借助同义词词典可知“美丽”和“漂亮”是同义词，从而得出这两句话语义相近。
  • 词义消歧：当一个词在不同语境中有不同含义时，依据同义词词典中该词不同义项对应的同义词集合，结合上下文选择合适的义项。例如，“苹果”既可以指水果，也可能是科技公司，通过上下文及同义词词典中相关义项的同义词来确定其准确含义。
• 优点：简单直观，对于明确的同义词关系能够快速识别和利用，不需要大量的训练数据。
• 缺点：依赖于预先构建的词典，覆盖面有限，难以涵盖所有的词汇和语义关系。对于新出现的词汇或特定领域的词汇，可能无法提供有效的语义信息。

3、基于计数的方法

• 原理：基于分布假设，即“一个词的意义由其经常出现的上下文所决定”。通过统计词汇在大规模文本语料库中的共现情况来衡量词汇之间的语义相似度。例如，在一个新闻语料库中，如果“银行”和“金融”经常同时出现在相近的语境中，那么可以认为这两个词在语义上具有一定关联。
• 实现方式：
  • 共现矩阵：构建一个词汇 - 词汇共现矩阵，行和列分别代表不同的词汇，矩阵元素表示两个词汇在语料库中的共现次数。例如，矩阵中第 $i$ 行第 $j$ 列的元素表示词汇 $i$ 和词汇 $j$ 的共现次数。
  • 向量空间模型：将每个词汇表示为一个向量，向量的维度对应于语料库中的其他词汇，向量元素是该词汇与对应维度词汇的共现次数或经过某种变换后的统计值。通过计算两个词汇向量之间的相似度（如余弦相似度）来衡量词汇的语义相似度。
• 应用场景：
  • 信息检索：在文档检索系统中，根据用户输入的关键词与文档中词汇的语义相似度，对文档进行排序，返回相关度较高的文档。例如，用户输入“计算机”，系统可通过计算“计算机”与文档中词汇的语义相似度，找到包含“电脑”等相关词汇的文档。
  • 文本分类：通过分析不同类别文本中词汇的共现模式，对新文本进行分类。例如，科技类文本中可能“技术”“创新”等词汇共现频繁，通过统计待分类文本中词汇与这些词汇的共现情况，判断其是否属于科技类文本。
• 优点：基于大规模真实语料库，能够自动获取词汇的语义信息，不需要人工标注大量数据。可以捕捉到词汇之间较为隐性的语义关系。
• 缺点：计算量较大，需要处理大规模的语料库和矩阵运算。对低频词汇的统计信息可能不准确，导致这些词汇的语义表示不可靠。而且，共现关系不一定完全等同于语义关系，可能存在误导。

4、基于推理的方法（word2vec）

• 原理：word2vec是一种基于神经网络的词向量表示模型，旨在通过对大量文本的学习，将每个词汇映射到一个低维向量空间中，使得语义相近的词汇在向量空间中距离较近。它有两种主要的模型架构：连续词袋模型（CBOW）和跳字模型（Skip - gram）。
  • CBOW模型：通过上下文词汇预测目标词汇。例如，给定上下文词汇“我”“喜欢”“阅读”，预测目标词汇“书籍”。模型通过对大量这样的上下文 - 目标词汇对进行学习，调整神经网络的参数，使得目标词汇的预测概率最大化。
  • Skip - gram模型：与CBOW相反，通过目标词汇预测上下文词汇。例如，给定目标词汇“苹果”，预测其周围可能出现的词汇“水果”“红色”等。同样通过最大化预测概率来学习词汇的向量表示。
• 应用场景：
  • 文本生成：在生成文本时，根据已有的词向量关系，生成语义连贯的文本。例如，在机器翻译中，利用源语言和目标语言的词向量，将源语言句子中的词汇映射到目标语言的相似语义词汇，生成翻译结果。
  • 知识图谱补全：在知识图谱中，通过词向量之间的关系，预测实体之间可能存在但未被标注的关系。例如，已知“苹果”与“水果”的词向量关系，以及“香蕉”的词向量，可以推断出“香蕉”与“水果”的关系。
• 优点：能够学习到词汇的分布式表示，有效捕捉词汇的语义特征和语义关系，在低维向量空间中体现词汇的相似性。生成的词向量可以很好地应用于各种NLP任务，通用性强。
• 缺点：训练过程需要大量的文本数据，对硬件资源和计算时间要求较高。模型学习到的词向量可能受到训练数据的限制，对于一些特定领域的专业词汇或新出现的词汇，可能无法准确表示其语义。

八、word2vec

1、CBOW模型

CBOW（Continuous Bag - of - Words）模型和Skip - gram模型是word2vec中两种重要的模型架构，它们都致力于将文本中的词汇转换为低维向量表示，以捕捉词汇的语义信息。以下将从模型原理、训练过程、优缺点以及应用场景等方面对它们进行详细介绍。

1. 模型原理
   • 核心思想：基于上下文预测目标词。其假设在给定上下文的情况下，目标词的出现概率仅取决于上下文词汇，而与这些上下文词汇的顺序无关，就像“词袋”一样，不考虑词序信息。
   • 输入与输出：输入是目标词周围的上下文词汇，输出是目标词。例如，对于句子“I like reading books”，如果以“books”为目标词，那么其上下文可以是“I”“like”“reading”。模型的任务是根据这三个上下文词汇预测出“books”。
2. 训练过程
   • 词向量表示：首先，每个词汇被映射到一个固定维度的向量空间，得到其初始词向量。假设词汇表大小为 $V$，词向量维度为 $d$，那么每个词汇都可以表示为一个 $d$ 维向量。
   • 上下文向量生成：将上下文词汇的词向量进行简单平均（或求和等其他聚合方式），得到一个上下文向量 $c$。例如，对于上述例子，将“I”“like”“reading”对应的词向量相加并平均，得到上下文向量 $c$。
   • 预测目标词：上下文向量 $c$ 通过一个线性变换（乘以权重矩阵 $W$），再经过Softmax函数，得到词汇表中每个词作为目标词的概率分布。Softmax函数的计算公式为 ${\hat{y}}_i=\frac{e^{z_i}}{{\sum }_{j=1}^V{e}^{z_j}}$，其中 $z_i$ 是线性变换后的第 $i$ 个值，${\hat{y}}_i$ 是预测第 $i$ 个词为目标词的概率。
   • 损失计算与优化：通过计算预测概率分布与真实分布（目标词对应的位置为1，其他位置为0）之间的交叉熵损失来衡量模型的预测误差。交叉熵损失函数为 $L=-{\sum }_{i=1}^V{y}_i\log ({\hat{y}}_i)$，其中 $y_i$ 是真实分布。然后使用随机梯度下降等优化算法，通过反向传播不断调整词向量和权重矩阵，使得损失函数最小化。在反向传播过程中，计算损失函数关于词向量和权重矩阵的梯度，并根据梯度更新参数。

2、skip-gram概率模型

1. 模型原理
   • 核心思想：与CBOW相反，Skip - gram模型是基于目标词预测上下文词汇。它认为目标词可以生成其周围的上下文词汇，通过最大化这种生成概率来学习词向量。
   • 输入与输出：输入是目标词，输出是目标词周围的上下文词汇。例如，对于句子“The dog runs fast”，如果以“runs”为目标词，那么输出可能是“The”“dog”“fast”等上下文词汇。
2. 训练过程
   • 词向量表示：与CBOW类似，每个词汇首先被映射到一个 $d$ 维向量空间，得到初始词向量。
   • 目标词向量处理：将目标词的词向量通过一个线性变换（乘以权重矩阵 $W$），得到一个中间向量。
   • 预测上下文词汇：中间向量再与词汇表中每个词汇的向量进行点积运算，经过Softmax函数得到每个词汇作为上下文词的概率分布。同样使用Softmax函数计算预测概率 ${\hat{y}}_i=\frac{e^{z_i}}{{\sum }_{j=1}^V{e}^{z_j}}$，这里 $z_i$ 是中间向量与第 $i$ 个词汇向量的点积结果。
   • 损失计算与优化：计算预测概率分布与真实分布（上下文词汇对应的位置为1，其他位置为0）之间的交叉熵损失，通过随机梯度下降等优化算法，利用反向传播调整词向量和权重矩阵，使损失函数最小化。在反向传播过程中，计算损失函数关于词向量和权重矩阵的梯度，并据此更新参数。

九、word2vec 的高速化

1、问题

在实际应用中，由于文本数据量通常非常庞大，直接训练word2vec模型可能会面临计算效率低下的问题。为实现word2vec的高速化，研究者提出了多种优化技术，主要从模型训练方式和负采样策略两方面入手。

2、模型训练方式优化

1. 层次Softmax
   • 原理：在原始的word2vec训练中，使用Softmax函数计算每个词作为预测结果的概率，其计算复杂度与词汇表大小 $V$ 成正比。层次Softmax通过构建一棵哈夫曼树来代替传统的Softmax计算，将词汇表中的每个词映射到哈夫曼树的叶子节点。对于每个叶子节点（即每个词），从根节点到该叶子节点存在唯一路径。在计算概率时，沿着这条路径进行，每次只需计算当前节点的两个子节点的概率，而不是像普通Softmax那样计算所有 $V$ 个词的概率。这样，计算复杂度从 $O(V)$ 降低到 $O(\log V)$。
   • 优势：大大减少了计算量，尤其在词汇表非常大时，显著提升了训练速度。同时，由于哈夫曼树是根据词频构建的，高频词对应的路径较短，计算概率的次数更少，进一步提高了效率。
2. 负采样
   • 原理：在训练过程中，每次更新不仅考虑正样本（目标词与上下文词的正确组合），还引入负样本（随机选择的与目标词不相关的词）。传统的Softmax计算需要对词汇表中的所有词计算概率，而负采样只关注正样本和少量负样本。具体来说，对于每个正样本 $(w_t,C(w_t))$（$w_t$ 是目标词，$C(w_t)$ 是上下文词），从词汇表中随机采样 $k$ 个负样本（通常 $k=5-20$）。在更新参数时，通过最大化正样本的出现概率，同时最小化负样本的出现概率来进行。这样，每次更新只涉及少量样本，而不是整个词汇表，大大减少了计算量。
   • 优势：有效降低了计算量，加快了训练速度。并且，负采样能够更好地捕捉词汇之间的局部语义关系，因为它更关注正样本和负样本之间的区分，使得模型对词汇的语义理解更加准确。

3、负采样策略优化

1. 基于词频的采样
   • 原理：在负采样中，不是均匀地从词汇表中随机选择负样本，而是根据词频进行采样。具体做法是，对于每个词 $w$，其被采样的概率与其词频 $f(w)$ 的某个幂次成正比。一种常见的做法是 $P(w)=\frac{f(w{)}^{\frac{3}{4}}}{{\sum }_{u\in V}f(u{)}^{\frac{3}{4}}}$。这样，高频词被采样为负样本的概率相对较高，低频词被采样的概率相对较低。
   • 优势：高频词在文本中出现频繁，对其进行更多的负采样可以让模型更好地学习到高频词与其他词的语义差异，避免模型过度关注高频词。同时，低频词虽然被采样次数少，但由于其本身出现频率低，也能在一定程度上保证模型对低频词的学习，从而平衡了不同频率词汇在训练中的作用，提高了模型整体的学习效果和训练速度。
2. 噪声对比估计（NCE）
   • 原理：NCE是一种与负采样相关的方法，它将词向量学习问题转化为一个二分类问题，即区分目标词与噪声词（负样本）。NCE假设噪声分布 $p_n(w)$，通过最小化目标函数来学习词向量。目标函数包括正样本（真实词对）的对数似然和负样本（噪声词对）的对数似然。在训练过程中，模型不断调整词向量，使得正样本的得分高于噪声样本的得分。与传统负采样不同的是，NCE通过引入噪声分布，使得模型在训练时能够更好地估计真实数据分布，从而提高模型的训练效率和性能。
   • 优势：NCE在处理大规模数据时表现出色，能够有效利用负样本信息，提高模型的训练速度和准确性。它不仅适用于word2vec模型，也可以应用于其他需要学习概率分布的模型中。

通过上述这些方法，word2vec在保持模型性能的同时，显著提高了训练速度，使其能够在大规模文本数据上高效运行，满足实际应用的需求。

十、RNN

循环神经网络（Recurrent Neural Network，RNN）是一类专门处理序列数据的神经网络，广泛应用于自然语言处理、语音识别、时间序列预测等领域。

1、语言模型

语言模型给出了单词序列发生的概率。就是使用概率来评估一个单词序列的可能性

2、RNN模型

a. 结构

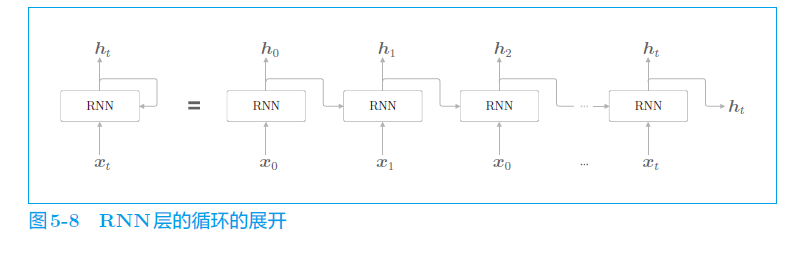
• 基本单元：RNN由一个个重复的模块组成，每个模块在序列的每个时间步接收输入，并基于当前输入和上一时刻的隐藏状态计算输出和新的隐藏状态。在每个时间步 $t$，输入为 $x_t$，上一时刻的隐藏状态为 $h_{t-1}$，模块通过特定的计算得到当前时刻的隐藏状态 $h_t$ 和输出 $y_t$。
• 隐藏状态：隐藏状态 $h_t$ 起到记忆的作用，它整合了之前时间步的信息，使得RNN能够捕捉序列中的长期依赖关系。隐藏状态通过不断更新，将过去的信息传递到当前时间步，从而帮助模型对当前输入进行更有效的处理。
• 权重共享：RNN的一个重要特点是在不同时间步上共享相同的权重。这意味着在处理序列中的每个元素时，使用的是相同的参数，大大减少了模型的参数数量，提高了模型的泛化能力，同时也使得模型能够处理不同长度的序列。

b. 工作原理

• 前向传播：在每个时间步 $t$，输入 $x_t$ 与上一时刻的隐藏状态 $h_{t-1}$ 首先被连接在一起，然后通过一个全连接层进行线性变换，得到一个中间结果 $z_t$。即 $z_t=W_{xh}{x}_t+W_{hh}{h}_{t-1}+b_h$，其中 $W_{xh}$ 是输入到隐藏层的权重矩阵，$W_{hh}$ 是隐藏层到隐藏层的权重矩阵，$b_h$ 是偏置向量。接着，$z_t$ 通过一个激活函数（如tanh）进行非线性变换，得到当前时刻的隐藏状态 $h_t=\tanh (z_t)$。最后，隐藏状态 $h_t$ 通过另一个全连接层得到输出 $y_t=W_{hy}{h}_t+b_y$，其中 $W_{hy}$ 是隐藏层到输出层的权重矩阵，$b_y$ 是偏置向量。如果是分类任务，$y_t$ 可能会经过Softmax函数得到各类别的概率分布。
• 反向传播：在训练过程中，RNN使用时间反向传播（Backpropagation Through Time，BPTT）算法来计算梯度。BPTT与传统的反向传播算法类似，但由于RNN在时间上的展开，梯度不仅要在网络的层之间反向传播，还要在时间步之间反向传播。通过计算损失函数（如分类任务中的交叉熵损失，回归任务中的均方误差损失）关于权重和偏置的梯度，使用随机梯度下降等优化算法来更新模型的参数，使得损失函数逐渐减小。

c.挑战

• 梯度消失和梯度爆炸：在反向传播过程中，由于梯度在时间步之间不断传递，当网络层数较多或时间步较长时，梯度可能会在传递过程中逐渐减小（梯度消失），导致较早时间步的信息无法有效地传递到较晚时间步，使得模型难以学习到长期依赖关系；或者梯度可能会不断增大（梯度爆炸），导致参数更新过大，模型无法收敛。
• 长期依赖问题：虽然RNN理论上能够处理长期依赖关系，但在实际应用中，由于梯度消失等问题，很难学习到序列中相距较远的元素之间的依赖关系。例如，在一个很长的句子中，模型可能很难记住句子开头的信息来理解句子结尾的内容。

为了解决这些问题，人们提出了一些改进的RNN结构，如长短期记忆网络（LSTM）和门控循环单元（GRU），它们通过引入特殊的门控机制，有效地缓解了梯度消失和长期依赖问题，在实际应用中取得了更好的效果。

e. 训练示例

每个词按顺序输入网络，先进行embedding，获取分布式表示；再进入RNN层，RNN向上方输出隐藏状态，向下一时刻的RNN输出隐藏状态。本层RNN经过Affine给Softmax

h. 模型评价指标

困惑度/分叉度：

表示标签所对应的预测出来的概率的倒数，概率越大，倒数越小，困惑度/分叉度越小。

十一、Gated RNN

上面说了简单 RNN 可能存在梯度消失和梯度爆炸的问题，本章对以上两个问题进行讨论解决。

1、简单RNN问题分析解决

a. 梯度爆炸

1. 梯度裁剪
   • 原理：与解决梯度消失问题中的梯度裁剪类似，通过设置一个阈值，当梯度的范数（如L2范数）超过该阈值时，对梯度进行缩放，使其范数等于阈值。这可以直接限制梯度的大小，防止梯度在反向传播过程中不断增大，从而避免梯度爆炸。
   • 效果：梯度裁剪是解决梯度爆炸问题的常用方法，它能够有效地控制梯度的增长，保证模型训练的稳定性，使模型能够正常收敛。
2. 正则化
   • 原理：在损失函数中添加正则化项，如L1正则化（权重的绝对值之和乘以一个正则化系数）或L2正则化（权重的平方和乘以一个正则化系数）。正则化项可以对权重进行约束，防止权重变得过大，从而减少梯度爆炸的风险。以L2正则化为例，在反向传播计算梯度时，除了计算损失函数关于权重的梯度外，还需要加上正则化项关于权重的梯度，使得权重在更新时更加稳健。
   • 效果：正则化不仅可以防止梯度爆炸，还能在一定程度上避免过拟合，提高模型的泛化能力。通过合理调整正则化系数，可以平衡模型的拟合能力和稳定性。

b. 梯度消失

1. 改进网络结构

   • LSTM（长短期记忆网络）：
     • 原理：LSTM引入了门控机制，包括输入门、遗忘门和输出门。遗忘门决定从上一时刻的隐藏状态中保留哪些信息，输入门控制当前输入的信息如何进入记忆单元，输出门则决定记忆单元中的哪些信息将用于生成当前时刻的输出。记忆单元可以看作是一个“传送带”，能够在时间步之间传递信息，减少信息在传递过程中的丢失。通过这些门控机制，LSTM能够更好地控制信息的流动，有效地解决梯度消失问题，从而学习到长序列中的长期依赖关系。
     • 效果：在许多自然语言处理任务（如机器翻译、文本生成）和时间序列预测任务中，LSTM表现出色，能够处理比简单RNN长得多的序列数据。
   • GRU（门控循环单元）：
     • 原理：GRU是LSTM的一种简化变体，它将输入门和遗忘门合并为更新门，同时将记忆单元和隐藏状态合并。GRU同样通过门控机制来控制信息的流动，更新门决定了前一时刻的隐藏状态和当前输入的信息在新的隐藏状态中的比例，重置门则控制了有多少过去的信息被丢弃。这种简化的结构在保持性能的同时，计算效率更高。
     • 效果：在实际应用中，GRU在处理长序列数据时也能有效避免梯度消失问题，并且由于其计算量相对较小，训练速度更快，在一些对计算资源和时间要求较高的场景中得到广泛应用。

2. 梯度裁剪

   • 原理：在反向传播计算出梯度后，检查梯度的范数（如L2范数）。如果梯度范数超过一个预先设定的阈值，就对梯度进行缩放，使其范数等于该阈值。这样可以防止梯度在反向传播过程中变得过小，从而在一定程度上缓解梯度消失问题。具体做法是，设梯度为 $g$，阈值为 $v$，如果 $\Vert g\Vert >v$，则更新梯度为 $g=\frac{v}{\Vert g\Vert }g$。
   • 效果：虽然梯度裁剪不能从根本上解决梯度消失问题，但它是一种简单有效的缓解方法，能够保证训练过程的稳定性，使得模型在一定程度上能够处理较长的序列数据。

3. 使用更好的初始化方法

   • 原理：选择合适的权重初始化方法可以使模型在训练初期处于一个相对较好的状态，减少梯度消失的可能性。例如，Xavier初始化方法（也称为Glorot初始化）根据输入和输出的维度来初始化权重，使得信号在网络中能够更均匀地流动，避免梯度在传播过程中迅速衰减。其初始化公式为：对于权重矩阵 $W$，其元素 $W_{ij}$ 从均匀分布 $U(-\sqrt{\frac{6}{n_{in}+n_{out}}},\sqrt{\frac{6}{n_{in}+n_{out}}})$ 中采样，其中 $n_{in}$ 是输入神经元的数量，$n_{out}$ 是输出神经元的数量。
   • 效果：合适的初始化方法有助于模型更快地收敛，在一定程度上缓解梯度消失问题，特别是在处理较深的RNN网络时，能够提高模型的训练效果。

2、LSTM

长短期记忆网络（Long Short - Term Memory，LSTM）是一种特殊的循环神经网络（RNN），由Sepp Hochreiter和Jürgen Schmidhuber于1997年提出，有效解决了传统RNN在处理长序列数据时遇到的梯度消失和长期依赖问题。以下从其结构、工作原理、应用场景等方面进行介绍：

结构

1. 细胞状态（Cell State）：

   • 这是LSTM的核心结构，类似于一条贯穿整个网络的传送带。细胞状态可以在时间步之间传递信息，并且通过门控机制进行信息的添加和删除，它能够保存长期信息，使得LSTM可以处理长序列数据中的长期依赖关系。

2. 门控单元：

   • 遗忘门（Forget Gate）：决定从上一时刻的细胞状态 $C_{t-1}$ 中丢弃哪些信息。它接收上一时刻的隐藏状态 $h_{t-1}$ 和当前时刻的输入 $x_t$ 作为输入，通过一个全连接层和Sigmoid激活函数，输出一个介于0到1之间的向量 $f_t$。其中，0表示完全丢弃相应信息，1表示完全保留。其计算公式为 $f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$，这里 $W_f$ 是权重矩阵，$b_f$ 是偏置向量，$\sigma$ 是Sigmoid函数。
   • 输入门（Input Gate）：控制当前时刻的新信息如何添加到细胞状态中。它同样接收 $h_{t-1}$ 和 $x_t$ 作为输入，通过一个全连接层和Sigmoid激活函数生成输入门向量 $i_t$，用于决定哪些新信息将被添加。同时，另一个全连接层和tanh激活函数生成一个候选细胞状态向量 ${\tilde{C}}_t$。输入门的计算公式为 $i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$，候选细胞状态的计算公式为 ${\tilde{C}}_t=\tanh (W_C\cdot [h_{t-1},x_t]+b_C)$，其中 $W_i$、$W_C$ 是权重矩阵，$b_i$、$b_C$ 是偏置向量。
   • 输出门（Output Gate）：决定细胞状态中的哪些信息将用于生成当前时刻的输出 $h_t$。它接收 $h_{t-1}$ 和 $x_t$ 作为输入，通过一个全连接层和Sigmoid激活函数生成输出门向量 $o_t$。同时，细胞状态 $C_t$ 通过tanh激活函数进行变换，然后与输出门向量 $o_t$ 相乘，得到当前时刻的隐藏状态 $h_t$。输出门的计算公式为 $o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$，隐藏状态的计算公式为 $h_t=o_t\cdot \tanh (C_t)$，其中 $W_o$ 是权重矩阵，$b_o$ 是偏置向量。

工作原理

1. 更新细胞状态：
   • 首先，遗忘门根据当前输入和上一时刻隐藏状态，决定从细胞状态 $C_{t-1}$ 中丢弃哪些信息，得到 $f_t\cdot C_{t-1}$。
   • 然后，输入门根据当前输入和上一时刻隐藏状态，决定将哪些新信息添加到细胞状态中。通过将输入门向量 $i_t$ 与候选细胞状态向量 ${\tilde{C}}_t$ 相乘，得到 $i_t\cdot {\tilde{C}}_t$。
   • 最后，将上述两个结果相加，得到更新后的细胞状态 $C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$。
2. 生成隐藏状态：
   • 输出门根据当前输入和上一时刻隐藏状态，决定细胞状态 $C_t$ 中的哪些信息将用于生成当前时刻的隐藏状态 $h_t$。通过将输出门向量 $o_t$ 与经过tanh激活函数变换后的细胞状态 $\tanh (C_t)$ 相乘，得到 $h_t=o_t\cdot \tanh (C_t)$。隐藏状态 $h_t$ 既可以作为当前时刻的输出，也可以传递到下一个时间步作为输入。

十二、基于RNN的文本生成

1、基于RNN/LSTM的文本生成

前面运用 RNNLM 进行各种应用：机器翻译等。RNN也能用于文本生成。

如果直接用简单 RNN 或者 LSTM，在网络输出的最后一层softmax后，利用概率分布进行输出单词（不是取最有可能的值，而是以概率地进行取值），虽然也能进行文本生成，但是可能效果比较差。

2、seq2seq

下面就介绍很牛的文本生成的模型——seq2seq，也称为 Encoder——Decoder 模型，即编码器——解码器模型。编码是基于某种规则进行信息转换的过程。解码时还原信息的过程。比如将字符 “A” 可以编码成1000001，然后可以将1000001解码成字符 “A”。 这个模型比较简单，可以快速学习。

序列到序列（Sequence to Sequence，简称Seq2Seq）模型是一种用于处理序列数据转换任务的深度学习模型架构，在自然语言处理、语音识别等多个领域有着广泛应用。以下从其模型结构、工作原理、应用场景和局限性等方面进行介绍。

模型结构

Seq2Seq模型主要由编码器（Encoder）和解码器（Decoder）两部分组成，中间通过上下文向量（Context Vector）进行连接。

1. 编码器：负责对输入序列进行编码，将其转换为一个固定长度的向量表示，即上下文向量。编码器通常是一个循环神经网络（RNN），如LSTM或GRU。在处理输入序列 $x=(x_1,x_2,\dots ,x_T)$ 时，编码器按时间步依次输入序列元素，每个时间步的隐藏状态会捕捉到当前及之前输入的信息。最终时刻的隐藏状态 $h_T$ 通常被作为上下文向量 $c$，它包含了整个输入序列的语义信息。
2. 解码器：利用编码器生成的上下文向量，生成目标序列。解码器同样是一个RNN结构，它以上下文向量 $c$ 作为初始隐藏状态，然后逐步生成输出序列 $y=(y_1,y_2,\dots ,y_{T^{\prime }})$。在每个时间步 $t$，解码器根据上一时刻的隐藏状态 $h_{t-1}$ 和生成的上一个词 $y_{t-1}$ 预测当前时刻的词 $y_t$。预测过程通常通过一个全连接层和Softmax函数，将隐藏状态映射到词汇表上的概率分布，选择概率最高的词作为输出。

工作原理

1. 编码过程：对于输入序列中的每个元素 $x_t$，编码器计算隐藏状态 $h_t$。以LSTM为例，在每个时间步 $t$，输入 $x_t$ 与上一时刻隐藏状态 $h_{t-1}$ 一同输入到LSTM单元中，通过遗忘门、输入门和输出门的控制，更新细胞状态 $C_t$ 和隐藏状态 $h_t$。当处理完整个输入序列后，最终的隐藏状态 $h_T$ 作为上下文向量 $c$，总结了输入序列的主要信息。
2. 解码过程：解码器以上下文向量 $c$ 作为初始隐藏状态 $h_0$ 开始生成输出序列。在每个时间步 $t$，解码器将上一时刻的隐藏状态 $h_{t-1}$ 和上一时刻生成的词 $y_{t-1}$（在第一个时间步，$y_{t-1}$ 可以是起始标记）作为输入，通过LSTM单元计算当前时刻的隐藏状态 $h_t$。然后，隐藏状态 $h_t$ 通过一个全连接层映射到词汇表大小的维度，再经过Softmax函数得到词汇表中每个词的生成概率。选择概率最高的词作为当前时刻生成的词 $y_t$。重复这个过程，直到生成结束标记（如“EOS”），表示输出序列生成完成。

应用场景

1. 机器翻译：将一种语言的句子作为输入序列，通过Seq2Seq模型转换为另一种语言的句子。编码器对源语言句子进行编码，解码器根据编码后的上下文向量生成目标语言句子，是机器翻译领域的常用模型架构。
2. 文本摘要：把一篇长文本作为输入序列，模型生成一个简短的摘要作为输出序列。编码器提取长文本的关键信息，解码器基于这些信息生成简洁的摘要，帮助用户快速获取文本的核心内容。
3. 对话系统：在聊天机器人等对话系统中，用户的输入作为输入序列，模型生成回复作为输出序列。Seq2Seq模型可以学习到对话中的语义理解和回复生成能力，实现人机对话交互。

局限性

1. 固定长度上下文向量限制：编码器将整个输入序列压缩为一个固定长度的上下文向量，在处理长序列时，可能无法有效地捕捉和表示所有信息，导致信息丢失，影响输出序列的质量。
2. 缺乏对输入序列的细粒度关注：解码器在生成输出时，主要依赖固定的上下文向量，难以动态地关注输入序列的不同部分。例如在机器翻译中，可能无法准确地将源语言句子中的不同部分与目标语言的对应部分进行匹配。为解决这些问题，后来引入了注意力机制（Attention Mechanism），它允许解码器在生成每个输出词时，动态地聚焦于输入序列的不同位置，从而提高模型性能。

3、seq2seq的改进

如果训练seq2seq进行加法计算，由于他是语言模型，不是计算器，所以可能性能不是很好。

对其进行改进的办法有两个：

a. 反转数据

比如数据如果有 5 + 75 反转之后就是 75 + 5

利用反转数据进行训练，可以提升精确度。

b. Peeky （偷窥）

对于解码器，他的输入只有编码器送过来的 h，直接输入到 LSTM 层中。那能不能更加充分地利用上这个 h 呢？

改进前：

改进后：

其实就是把 h 不单单作为隐藏状态传入 LSTM，它将与 LSTM 的输入、Affine 层的输入进行向量拼接，然后作为输入。

就是把 h 多层共享，而非私有。或许能做出更加正确的判断。

4、LSTM 的应用

• 机器翻译
• 自动摘要
• 问答系统
• 邮件自动回复

十三、Attention

1、注意力机制

Seq2Seq的不足

1. 信息损失问题
   • 固定长度上下文向量局限：Seq2Seq模型通过编码器将输入序列压缩为一个固定长度的上下文向量，以此作为解码器生成输出序列的依据。然而，当输入序列较长时，这种固定长度的表示方式难以容纳所有信息，会导致信息丢失。例如在长文本的机器翻译任务中，编码器可能无法将长句中的所有语义细节都编码到上下文向量中，使得解码器在生成译文时缺乏关键信息，译文质量下降。
   • 长期依赖处理困难：虽然Seq2Seq模型中的RNN结构（如LSTM或GRU）在一定程度上缓解了长期依赖问题，但在处理极长序列时，上下文向量依然难以捕捉到序列开头的信息。例如在处理长篇小说的文本摘要任务中，开头部分的关键信息可能无法有效地传递到解码器，导致生成的摘要不能全面反映小说的内容。
2. 解码缺乏针对性
   • 统一依赖上下文向量：解码器在生成输出序列的每个元素时，都依赖同一个固定的上下文向量。这意味着解码器无法根据生成过程中不同时刻的需求，动态地关注输入序列的不同部分。比如在翻译中，对于源语言句子中的不同词汇，在目标语言中可能需要不同的翻译策略，而Seq2Seq模型难以针对每个输出词灵活地从输入序列中提取最相关的信息。

注意力机制

1. 基本原理
   • 动态权重分配：注意力机制的核心思想是让解码器在生成每个输出词时，能够动态地计算输入序列中各个位置与当前输出词的关联程度，即计算注意力权重。这些权重表示了输入序列中每个元素对生成当前输出词的重要性。例如，在机器翻译中，当生成目标语言句子中的某个词时，注意力机制可以使模型更关注源语言句子中与该词语义相关的部分。
   • 加权求和生成上下文向量：根据计算得到的注意力权重，对输入序列的隐藏状态进行加权求和，从而生成一个针对当前输出词的动态上下文向量。这个动态上下文向量会随着输出词的生成而变化，能够更好地捕捉与当前输出相关的信息。具体计算过程如下：
     • 假设编码器的隐藏状态为 $h_1,h_2,\dots ,h_T$，解码器在生成第 $t$ 个输出词时，首先计算注意力分数 $e_{t,i}$，它表示解码器当前状态与编码器第 $i$ 个隐藏状态的相关性，通常通过一个前馈神经网络或点积运算得到。
     • 然后，通过Softmax函数将注意力分数转换为注意力权重 ${\alpha }_{t,i}$，即 ${\alpha }_{t,i}=\frac{\exp (e_{t,i})}{{\sum }_{j=1}^T\exp (e_{t,j})}$。
     • 最后，根据注意力权重对编码器的隐藏状态进行加权求和，得到动态上下文向量 $c_t={\sum }_{i=1}^T{\alpha }_{t,i}{h}_i$。

2、在Seq2Seq中的应用方式

• 改进解码过程：在Seq2Seq模型中引入注意力机制后，解码器在生成每个输出词时，不再仅仅依赖固定的上下文向量，而是使用动态生成的上下文向量。具体来说，在解码器的每个时间步，将动态上下文向量与解码器的上一时刻隐藏状态一起作为输入，计算当前时刻的隐藏状态和输出词的概率分布。这样，解码器能够根据生成的不同阶段，动态地聚焦于输入序列的不同部分，从而更准确地生成输出序列。

• 优势

  • 提高信息利用率：注意力机制通过动态关注输入序列的不同部分，使得解码器能够更有效地利用输入序列中的信息，减少信息损失。在处理长序列时，能够更准确地捕捉到与当前输出相关的信息，从而提高模型在各种序列转换任务中的性能，如机器翻译、文本摘要等任务的质量得到显著提升。

  • 增强模型可解释性：注意力权重直观地反映了输入序列中各个元素与输出序列中每个元素的关联程度。通过分析注意力权重，可以了解模型在生成过程中关注的重点，从而为模型的决策过程提供一定的解释。例如，在机器翻译中，可以通过可视化注意力权重，观察源语言句子中的哪些词对生成目标语言句子中的某个词起到了关键作用。

3、Transformer

Transformer是谷歌团队在 2017 年论文《Attention Is All You Need》中提出的一种全新的深度学习架构，主要用于处理序列数据，在自然语言处理、计算机视觉等多个领域都取得了巨大成功。以下是对它的详细介绍：

1. 基本架构：Transformer 架构主要由编码器（Encoder）和解码器（Decoder）两部分组成。
   • 编码器：由多个相同的层堆叠而成，每个层包含两个子层：多头自注意力机制（Multi-Head Attention）和前馈神经网络（Feed Forward Neural Network）。在多头自注意力机制中，输入序列的每个元素都可以关注到序列中的其他元素，从而捕捉元素之间的关系，生成包含上下文信息的特征表示。接着，这些特征表示会输入到前馈神经网络中进行进一步的非线性变换。此外，每个子层都使用了残差连接（Residual Connection）和层归一化（Layer Normalization）技术，以帮助训练过程更加稳定。
   • 解码器：同样由多个相同的层堆叠构成，每个层包含三个子层：多头自注意力机制、编码器-解码器注意力机制（Encoder-Decoder Attention）和前馈神经网络。解码器的多头自注意力机制与编码器类似，但在生成序列时会进行掩码操作，以确保每个位置只能关注到之前已经生成的位置。编码器-解码器注意力机制使得解码器能够关注编码器的输出，将编码器提取的源序列特征与解码器当前的状态相结合。最后，通过前馈神经网络生成最终的输出。
2. 核心机制——注意力机制（Attention Mechanism）：Transformer 的核心是注意力机制，特别是多头自注意力机制。注意力机制的本质是计算输入序列中元素之间的相似度，以确定每个元素在不同位置的重要性权重。多头自注意力机制则是将注意力机制并行运行多个头（Head），每个头学习到不同的特征表示子空间，然后将这些子空间的结果拼接起来，使得模型能够捕捉到更丰富的信息。计算注意力分数的公式一般为 (Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V)，其中 (Q)（Query）、(K)（Key）、(V)（Value）是输入的不同表示，(d_k) 是 (K) 的维度。
3. 优点：
   • 长距离依赖处理能力强：相比传统的循环神经网络（RNN），Transformer 能够更有效地处理长序列数据中的长期依赖关系，因为它可以直接计算序列中任意两个位置之间的注意力，不受序列长度的限制。
   • 并行计算能力高：RNN 由于其循环结构，只能顺序计算，难以并行处理。而 Transformer 的各个位置之间的计算相互独立，因此可以在多个位置上同时进行计算，大大提高了训练和推理的效率，适合在 GPU 等并行计算设备上运行。
   • 可解释性相对较好：注意力机制的输出可以直观地展示输入序列中不同位置之间的关联程度，通过可视化注意力分数，能够一定程度上理解模型的决策过程和对不同信息的关注重点。
4. 应用领域：
   • 自然语言处理：是 Transformer 应用最广泛的领域，包括机器翻译、文本摘要、问答系统、语言模型（如 GPT 系列、BERT 等）等。例如，BERT 模型基于 Transformer 编码器，在大量无监督文本上进行预训练后，在各种自然语言处理任务中取得了优异的成绩。
   • 计算机视觉：近年来，Transformer 也逐渐应用于计算机视觉领域，如图像分类、目标检测、图像分割等。例如，Vision Transformer（ViT）将图像划分为多个小块，然后将这些小块视为序列元素，利用 Transformer 架构进行处理。
   • 语音处理：在语音识别、语音合成等任务中也开始采用 Transformer 架构，能够有效处理语音信号中的时间序列信息。

Transformer 以其独特的架构和强大的性能，为深度学习领域带来了新的突破和发展方向，推动了多个领域的技术进步。