小白的深度学习日常3

李哥的深度学习篇3

对应第4节分类任务
通过前面的学习，我们已经学习了全连接神经网络，接下来要学习卷积神经网络CNN
前面用全连接问题主要解决的是回归预测问题。

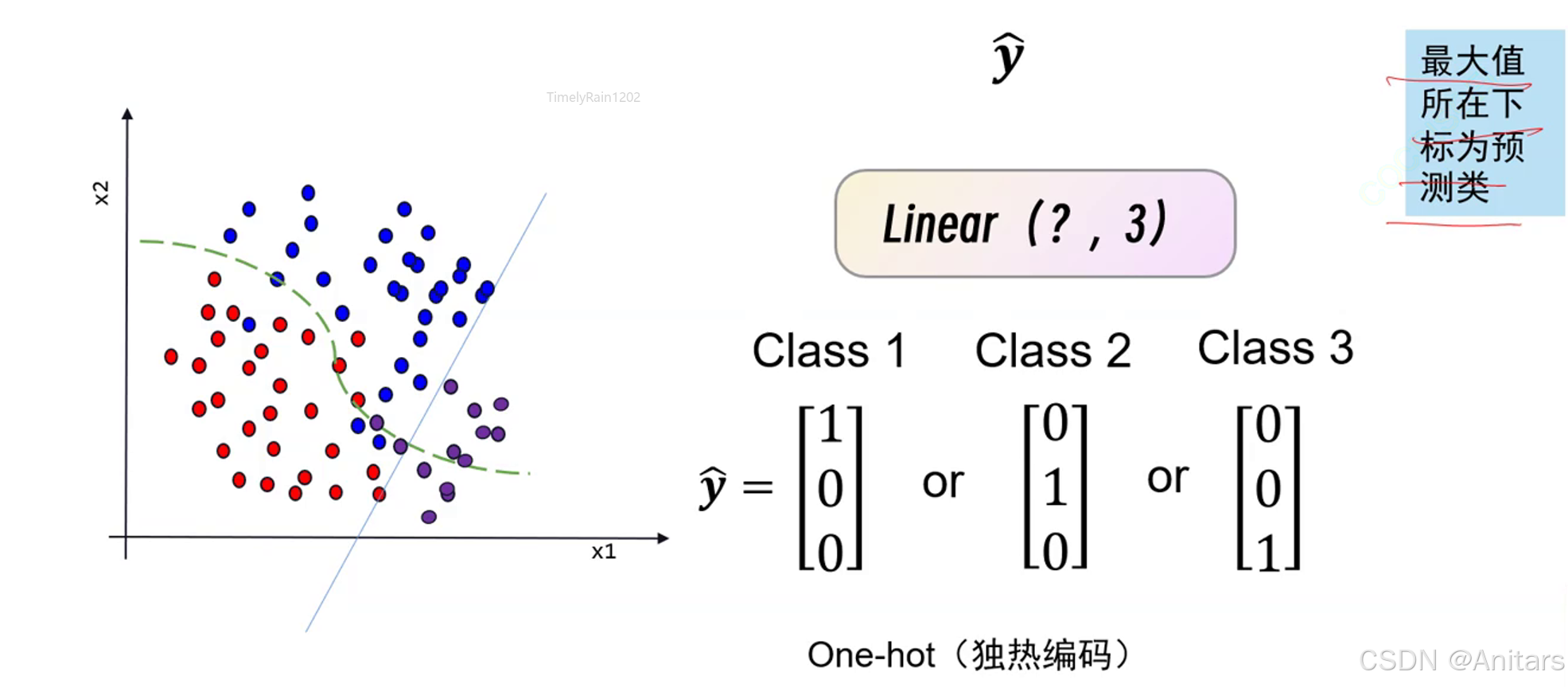
现实中除了预测问题，还有分类问题：


如何做分类的输出？用独热编码表示。
独热编码（One-Hot Encoding）是一种用于处理分类数据的编码方式。在机器学习和深度学习中，很多算法不能直接处理分类数据，因为它们期望输入是数值型的。独热编码将分类变量转换为一种可以被机器学习算法理解的格式。
原理：独热编码的原理是将每个类别映射到一个二进制向量，其中只有一个元素为1，其余元素为0。这个1所在的位置表示该样本属于哪个类别。
示例：假设有一个分类变量“颜色”，它有三个可能的取值：“红色”、“绿色”和“蓝色”。使用独热编码，这三个类别将被转换为以下向量：

• “红色”：[1, 0, 0]
• “绿色”：[0, 1, 0]
• “蓝色”：[0, 0, 1]
  
  需要注意，进行图片分类的时候，所有图片的大小需要相同。
  

交叉熵损失：交叉熵损失（Cross-Entropy Loss）是一种常用的损失函数，主要用于衡量两个概率分布之间的差异。在机器学习和深度学习中，特别是在分类问题中，交叉熵损失被广泛应用。

交叉熵损失的原理基于信息论中的交叉熵概念。对于两个概率分布 $p$ 和 $q$，它们之间的交叉熵定义为：
$$H(p,q)=-\sum _{x}p(x)\log q(x)$$

在分类问题中，$p$ 通常是真实的标签分布（one-hot编码），而 $q$ 是模型预测的概率分布。交叉熵损失衡量了模型预测的概率分布与真实标签分布之间的差异。
示例：假设有一个三分类问题，真实标签为 $[0,1,0]$，模型预测的概率分布为 $[0.1,0.7,0.2]$。则交叉熵损失计算如下：
$$H(p,q)=-(0\times \log 0.1+1\times \log 0.7+0\times \log 0.2)\approx 0.3567$$
在Python中，可以使用 torch.nn.CrossEntropyLoss（PyTorch） 或 tf.keras.losses.CategoricalCrossentropy（TensorFlow） 来计算交叉熵损失。

交叉熵损失主要应用于以下场景：

• 多分类问题：如图像分类、文本分类等。
• 神经网络的训练：作为损失函数，用于优化模型参数。

如果使用全连接，224×224×3×1000 + 1000个参数量，参数量过大，容易过拟合，所以我们使用卷积神经网络。

用卷积核在特征图上不断滑动，相乘并相加特到新的特征值，最后得到新的特征图，移动的距离称作步长。

C：chennel，一般指层数，厚度
W：width，宽度
H：height，高度

卷积减小特征图尺寸解决办法：填充0，Zeropadding。在周围填充数圈0。

感受野：简单来说，就是卷积核能看到的大小。
感受野（Receptive Field）是卷积神经网络（CNN）中的一个重要概念，用于描述网络中某一层的一个神经元能够“看到”的输入图像的区域大小。感受野的大小和位置决定了神经元能够捕捉到的特征的范围和细节。

卷积的过程：不同的卷积核对应不同的特征。

在卷积神经网络（CNN）中，不同的卷积核通常对应不同的特征。每个卷积核可以看作是一个特征提取器，用于检测输入数据（如图像）中的特定模式或特征。对于复杂的对象（如鸟），不同的卷积核可能会捕捉到对象的不同部分或特征，例如鸟头、鸟嘴、鸟爪等。

1. 卷积核的作用

   • 每个卷积核在输入数据上滑动，计算局部区域的点积，生成特征图（Feature Map）。
   • 不同的卷积核具有不同的权重，因此会提取不同的特征。
   • 例如：
     • 一个卷积核可能对边缘敏感，提取图像中的边缘特征。
     • 另一个卷积核可能对纹理敏感，提取图像中的纹理特征。

2. 卷积核与特征的关系

   • 浅层卷积核：通常提取低级特征，如边缘、角点、颜色等。
     • 例如，在鸟的图像中，浅层卷积核可能提取鸟的轮廓或羽毛的纹理。
   • 深层卷积核：通过组合低级特征，提取更高级的语义特征。
     • 例如，深层卷积核可能提取鸟头、鸟嘴、鸟爪等局部特征，甚至整个鸟的形状。

特征图如何变小？

1. 扩大步长
2. 依靠池化
   

池化（Pooling）是卷积神经网络（CNN）中的一种重要操作，用于减少特征图的空间尺寸，同时保留重要的特征信息。 池化操作通常在卷积层之后应用，有助于降低计算量、控制过拟合，并增强模型的鲁棒性。

池化的类型

1. 最大池化（Max Pooling）：在每个池化窗口内，取最大值作为输出。这种方法能够保留最显著的特征，对于图像中的边缘、纹理等特征的提取非常有效。
2. 平均池化（Average Pooling）：在每个池化窗口内，取平均值作为输出。平均池化能够平滑特征图，对整体特征的提取有一定帮助。

池化的作用

1. 降维：通过减少特征图的尺寸，降低后续层的计算量，提高计算效率。
2. 特征不变性：池化操作具有一定的平移不变性，即当输入图像发生微小的平移时，池化后的结果基本保持不变，这有助于提高模型的鲁棒性。
3. 防止过拟合：池化操作可以减少特征的数量，从而降低模型的复杂度，有助于防止过拟合。

卷积完成之后，先展平，后全连接。将卷积层和池化层提取的特征进行整合，输出最终的预测结果。

softmax：Softmax是一种常用的激活函数，主要用于多分类问题。它将一个包含任意实数的K维向量“压缩”到另一个K维实向量中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。这样，输出向量可以被解释为一个概率分布。

综合流程图

数据集：

经典神经网络：

Dropout是一种在神经网络中常用的正则化技术，用于防止过拟合。 Dropout通过在训练过程中随机丢弃一部分神经元，使得模型在训练时不能过于依赖某些特定的神经元，从而提高模型的泛化能力。

Dropout的原理基于集成学习的思想。在每次训练迭代中，Dropout以一定的概率（通常为0.5）随机将一部分神经元的输出设置为0，即“丢弃”这些神经元。这样，每次训练时网络的结构都会有所不同，相当于训练了多个不同的子网络。在测试时，所有神经元都被使用，但它们的输出会根据训练时的丢弃概率进行缩放，以保持期望输出不变。

归一化（Normalization）是一种数据预处理技术，用于将数据缩放到一个特定的范围，通常是[0, 1]或[-1, 1]。归一化的目的是消除数据的量纲和尺度差异，使得不同特征之间具有可比性，从而提高机器学习模型的性能和稳定性。

1. 最小-最大归一化（Min-Max Normalization）：

• 公式：X_normalized = (X - X_min) / (X_max - X_min)
• 作用：将数据缩放到[0, 1]的范围内。
• 适用场景：适用于数据分布较为均匀的情况。

2. Z-Score归一化（标准化）：

• 公式：X_normalized = (X - mean(X)) / std(X)
• 作用：将数据转换为均值为0，标准差为1的标准正态分布。
• 适用场景：适用于数据分布较为复杂的情况。

4. 批归一化（Batch Normalization）：

• 公式：X_normalized = (X - mean(X_batch)) / std(X_batch)
• 作用：在每个批次的数据上进行归一化，使得每个批次的均值为0，方差为1。
• 适用场景：适用于深度神经网络的训练过程，有助于加速收敛和提高模型的稳定性。

5. 层归一化（Layer Normalization）：

• 公式：X_normalized = (X - mean(X_layer)) / std(X_layer)
• 作用：在每个层的特征上进行归一化，使得每个层的均值为0，方差为1。
• 适用场景：适用于循环神经网络（RNN）和长短期记忆网络（LSTM）等序列模型。

class MyAlexNet(nn.Module):
    def __init__(self):
        super(MyAlexNet, self).__init__()
        self.relu = nn.ReLU()
        self.drop = nn.Dropout(0.5)

        self.conv1 = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=11, stride=4,padding=2)
        self.pool1 = nn.MaxPool2d(3, stride=2)
        self.conv2 = nn.Conv2d(64,192,5,1,2)
        self.pool2 = nn.MaxPool2d(3, stride=2)

        self.conv3 = nn.Conv2d(192,384,3,1,1)

        self.conv4 = nn.Conv2d(384,256,3,1,1)

        self.conv5 = nn.Conv2d(256, 256, 3, 1, 1)

        self.pool3 = nn.MaxPool2d(3, stride=2)
        self.adapool = nn.AdaptiveAvgPool2d(output_size=6)

        self.fc1 = nn.Linear(9216,4096)

        self.fc2 = nn.Linear(4096,4096)

        self.fc3 = nn.Linear(4096,1000)

    def forward(self,x):

        x = self.conv1(x)
        x = self.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool2(x)


        x = self.conv3(x)
        x = self.relu(x)

        x = self.conv4(x)
        x = self.relu(x)

        x = self.conv5(x)
        x = self.relu(x)
        x = self.pool3(x)

        x= self.adapool(x)
        x = x.view(x.size()[0], -1)

        x = self.fc1(x)
        x = self.relu(x)

        x = self.fc2(x)
        x = self.relu(x)

        x = self.fc3(x)
        x = self.relu(x)

        return x

卷积层1：64个11x11的卷积核，每个卷积核有3个通道（对应RGB图像），因此这一层的参数数量为64x11x11x3 + 64（偏置）= 23,296个。
卷积层2：192个5x5的卷积核，每个卷积核有96个通道（上一层的输出通道数），因此这一层的参数数量为192x5x5x64 + 192（偏置）= 307,392个。
卷积层3：384个3x3的卷积核，每个卷积核有256个通道，因此这一层的参数数量为384x3x3x192 + 192（偏置）= 663,744个。
卷积层4：384个3x3的卷积核，每个卷积核有384个通道，因此这一层的参数数量为256x3x3x384 + 384（偏置）= 885,120个。
卷积层5：256个3x3的卷积核，每个卷积核有384个通道，因此这一层的参数数量为256x3x3x256 + 256（偏置）= 590,080个。
全连接层1：4096个神经元，输入特征数为上一层的输出特征数（假设为9216），因此这一层的参数数量为4096x9216 + 4096（偏置）= 37,752,832个。
全连接层2：4096个神经元，因此这一层的参数数量为4096x4096 + 4096（偏置）= 16,781,312个。
全连接层3：1000个神经元（对应1000个类别），因此这一层的参数数量为4096x1000 + 1000（偏置）= 4,097,000个。

原理：2个3×3的卷积核能代替一个5×5的卷积核

class vggLayer(nn.Module):
    def __init__(self,in_cha, mid_cha, out_cha):
        super(vggLayer, self).__init__()
        self.relu = nn.ReLU()
        self.pool = nn.MaxPool2d(2)
        self.conv1 = nn.Conv2d(in_cha, mid_cha, 3, 1, 1)
        self.conv2 = nn.Conv2d(mid_cha, out_cha, 3, 1, 1)

    def forward(self,x):
        x = self.conv1(x)
        x= self.relu(x)
        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool(x)


        return x



class MyVgg(nn.Module):
    def __init__(self):
        super(MyVgg, self).__init__()

        self.layer1 = vggLayer(3, 64, 64)

        self.layer2 = vggLayer(64, 128, 128)

        self.layer3 = vggLayer(128, 256, 256)

        self.layer4 = vggLayer(256, 512, 512)

        self.layer5 = vggLayer(512, 512, 512)
        self.adapool = nn.AdaptiveAvgPool2d(7)
        self.relu = nn.ReLU()
        self.fc1 = nn.Linear(25088, 4096)
        self.fc2 = nn.Linear(4096, 4096)
        self.fc3 = nn.Linear(4096, 1000)

    def forward(self,x):

        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)
        x = self.layer5(x)
        x = self.adapool(x)

        x= self.adapool(x)
        x = x.view(x.size()[0], -1)

        x = self.fc1(x)
        x = self.relu(x)

        x = self.fc2(x)
        x = self.relu(x)

        x = self.fc3(x)
        x = self.relu(x)

        return x

layer1：
conv1：$(3\times 64\times 3\times 3+64)=1792$
conv2：$(64\times 64\times 3\times 3+64)=36928$
总参数量：$1792+36928=38720$

layer2：
conv1：$(64\times 128\times 3\times 3+128)=73856$
conv2：$(128\times 128\times 3\times 3+128)=147584$
总参数量：$73856+147584=221440$

layer3：
conv1：$(128\times 256\times 3\times 3+256)=295168$
conv2：$(256\times 256\times 3\times 3+256)=590080$
总参数量：$295168+590080=885248$

layer4：
conv1：$(256\times 512\times 3\times 3+512)=1180160$
conv2：$(512\times 512\times 3\times 3+512)=2359808$
总参数量：$1180160+2359808=3539968$

layer5：
conv1：$(512\times 512\times 3\times 3+512)=2359808$
conv2：$(512\times 512\times 3\times 3+512)=2359808$
总参数量：$2359808+2359808=4719616$

卷积层总参数量：$38720+221440+885248+3539968+4719616=9404992$

全连接层总参数量：
fc1：$(25088\times 4096+4096)=102764544$
fc2：$(4096\times 4096+4096)=16781312$
fc3：$(4096\times 1000+1000)=4097000$
全连接层总参数量：$102764544+16781312+4097000=123642856$

MyVgg 的总参数量：$9404992+123642856=133047848$

1x1卷积在深度学习中具有多种重要作用，主要包括以下几个方面：

1. 降维和升维：
   • 降维：通过1x1卷积，可以减少特征图的通道数，从而降低模型的计算量和参数量。例如，在一个具有256个通道的特征图上应用1x1卷积，将通道数减少到128，可以显著减少后续层的计算量。
   • 升维：相反，1x1卷积也可以增加特征图的通道数，从而增加模型的表达能力。例如，在一个具有128个通道的特征图上应用1x1卷积，将通道数增加到256，可以使模型学习到更复杂的特征表示。
2. 特征融合：
   • 1x1卷积可以用于融合不同通道的特征信息。在卷积神经网络中，不同通道的特征图可能包含不同的语义信息，通过1x1卷积，可以将这些信息进行融合，从而提高模型的性能。
3. 非线性变换：
   • 在1x1卷积之后，通常会应用激活函数（如ReLU），从而引入非线性变换。这有助于模型学习到更复杂的特征表示，提高模型的表达能力。
4. 减少计算量：
   • 在一些网络结构中，如Inception模块，1x1卷积可以用于减少计算量。通过先应用1x1卷积减少通道数，再进行其他卷积操作，可以显著降低计算成本。
5. 调整特征图的空间尺寸：
   • 虽然1x1卷积本身不会改变特征图的空间尺寸（高度和宽度），但它可以与其他卷积层或池化层结合使用，从而调整特征图的空间尺寸。

残差连接（Residual Connection）是一种在深度学习中常用的技术，特别是在深度卷积神经网络（CNN）中。它的主要作用是解决深度神经网络中的梯度消失和梯度爆炸问题，从而使得训练更深的网络成为可能。

原理：残差链接的基本思想是在神经网络的某一层中，将输入直接加到输出上，形成一个“短路连接”。这样做的好处是，即使在网络很深的情况下，梯度也能够通过这个短路连接直接传播到较早的层，从而避免了梯度消失或梯度爆炸的问题。

# 导入必要的库
import torch
import torch.nn as nn
import torchvision.models as models

# 加载预训练的ResNet-18模型
resNet = models.resnet18()
# 打印模型结构
print(resNet)

# 定义残差块（Residual Block）
class Residual_block(nn.Module):  #@save
    def __init__(self, input_channels, out_channels, down_sample=False, strides=1):
        super().__init__()
        # 第一个卷积层，输入通道数为input_channels，输出通道数为out_channels，卷积核大小为3，填充为1，步幅为strides
        self.conv1 = nn.Conv2d(input_channels, out_channels, kernel_size=3, padding=1, stride=strides)
        # 第二个卷积层，输入通道数为out_channels，输出通道数为out_channels，卷积核大小为3，填充为1，步幅为1
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1, stride=1)
        # 如果输入通道数不等于输出通道数，则需要一个1x1的卷积层来调整通道数
        if input_channels != out_channels:
            self.conv3 = nn.Conv2d(input_channels, out_channels, kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        # 第一个批归一化层
        self.bn1 = nn.BatchNorm2d(out_channels)
        # 第二个批归一化层
        self.bn2 = nn.BatchNorm2d(out_channels)
        # ReLU激活函数
        self.relu = nn.ReLU()

    def forward(self, X):
        # 第一个卷积层，经过批归一化和ReLU激活函数
        out = self.relu(self.bn1(self.conv1(X)))
        # 第二个卷积层，经过批归一化
        out = self.bn2(self.conv2(out))
        # 如果需要调整通道数，则对输入进行卷积操作
        if self.conv3:
            X = self.conv3(X)
        # 残差连接，将输入和输出相加
        out += X
        # 经过ReLU激活函数
        return self.relu(out)

# 定义自定义的ResNet-18模型
class MyResNet18(nn.Module):
    def __init__(self):
        super(MyResNet18, self).__init__()
        # 第一个卷积层，输入通道数为3，输出通道数为64，卷积核大小为7，步幅为2，填充为3
        self.conv1 = nn.Conv2d(3, 64, 7, 2, 3)
        # 第一个批归一化层
        self.bn1 = nn.BatchNorm2d(64)
        # 第一个最大池化层，池化核大小为3，步幅为2，填充为1
        self.pool1 = nn.MaxPool2d(3, stride=2, padding=1)
        # ReLU激活函数
        self.relu = nn.ReLU()

        # 第一个残差块，包含两个残差块，输入通道数为64，输出通道数为64
        self.layer1 = nn.Sequential(
            Residual_block(64, 64),
            Residual_block(64, 64)
        )
        # 第二个残差块，包含两个残差块，输入通道数为64，输出通道数为128，步幅为2
        self.layer2 = nn.Sequential(
            Residual_block(64, 128, strides=2),
            Residual_block(128, 128)
        )
        # 第三个残差块，包含两个残差块，输入通道数为128，输出通道数为256，步幅为2
        self.layer3 = nn.Sequential(
            Residual_block(128, 256, strides=2),
            Residual_block(256, 256)
        )
        # 第四个残差块，包含两个残差块，输入通道数为256，输出通道数为512，步幅为2
        self.layer4 = nn.Sequential(
            Residual_block(256, 512, strides=2),
            Residual_block(512, 512)
        )
        # 展平层
        self.flatten = nn.Flatten()
        # 自适应平均池化层，输出大小为1x1
        self.adv_pool = nn.AdaptiveAvgPool2d(1)
        # 全连接层，输入大小为512，输出大小为1000
        self.fc = nn.Linear(512, 1000)

    def forward(self, x):
        # 第一个卷积层，经过批归一化和ReLU激活函数
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        # 第一个最大池化层
        x = self.pool1(x)

        # 第一个残差块
        x = self.layer1(x)
        # 第二个残差块
        x = self.layer2(x)
        # 第三个残差块
        x = self.layer3(x)
        # 第四个残差块
        x = self.layer4(x)

        # 自适应平均池化层
        x = self.adv_pool(x)
        # 展平层
        x = self.flatten(x)
        # 全连接层
        x = self.fc(x)

        return x

# 创建自定义的ResNet-18模型实例
myres = MyResNet18()

# 计算模型参数数量
def get_parameter_number(model):
    # 计算总参数数量
    total_num = sum(p.numel() for p in model.parameters())
    # 计算可训练参数数量
    trainable_num = sum(p.numel() for p in model.parameters() if p.requires_grad)
    # 返回总参数数量和可训练参数数量
    return {'Total': total_num, 'Trainable': trainable_num}

# 打印自定义模型的第一个残差块的参数数量
print(get_parameter_number(myres.layer1))
# 打印自定义模型的第一个残差块的第一个卷积层的参数数量
print(get_parameter_number(myres.layer1[0].conv1))
# 打印预训练模型的第一个残差块的第一个卷积层的参数数量
print(get_parameter_number(resNet.layer1[0].conv1))

# 生成一个随机输入张量，大小为1x3x224x224
x = torch.rand((1, 3, 224, 224))
# 将输入张量传递给预训练模型，得到输出
out = resNet(x)
# 将输入张量传递给自定义模型，得到输出
out = myres(x)

1. 第一个卷积层 conv1
   nn.Conv2d(3, 64, 7, 2, 3)
   参数量：$(3\times 64\times 7\times 7+64)=9472$
2. 第一个批归一化层 bn1
   nn.BatchNorm2d(64)
   参数量：$2\times 64=128$
3. 第一个最大池化层 pool1
   nn.MaxPool2d(3, stride=2, padding=1)
   参数量：$0$（池化层没有可学习的参数）
4. 第一个残差块 layer1
   包含两个 Residual_block(64, 64)
   每个 Residual_block 中的卷积层和批归一化层参数：
   conv1：$(64\times 64\times 3\times 3+64)=36928$
   conv2：$(64\times 64\times 3\times 3+64)=36928$
   bn1：$2\times 64=128$
   bn2：$2\times 64=128$
   两个 Residual_block 的总参数量：$(36928+36928+128+128)\times 2=148672$
5. 第二个残差块 layer2
   包含两个 Residual_block(64, 128, strides=2)
   每个 Residual_block 中的卷积层和批归一化层参数：
   conv1：$(64\times 128\times 3\times 3+128)=73856$
   conv2：$(128\times 128\times 3\times 3+128)=147584$
   bn1：$2\times 128=256$
   bn2：$2\times 128=256$
   conv3：$(64\times 128\times 1\times 1+128)=8320$（因为输入通道数和输出通道数不同，需要 conv3）
   两个 Residual_block 的总参数量：$(73856+147584+256+256+8320)\times 2=460352$
6. 第三个残差块 layer3
   包含两个 Residual_block(128, 256, strides=2)
   每个 Residual_block 中的卷积层和批归一化层参数：
   conv1：$(128\times 256\times 3\times 3+256)=295168$
   conv2：$(256\times 256\times 3\times 3+256)=590080$
   bn1：$2\times 256=512$
   bn2：$2\times 256=512$
   conv3：$(128\times 256\times 1^2+256)=33024$（因为输入通道数和输出通道数不同，需要 conv3）
   两个 Residual_block 的总参数量：$(295168+590080+512+512+33024)\times 2=1838592$
7. 第四个残差块 layer4
   包含两个 Residual_block(256, 512, strides=2)
   每个 Residual_block 中的卷积层和批归一化层参数：
   conv1：$(256\times 512\times 3\times 3+512)=1180160$
   conv2：$(512\times 512\times 3\times 3+512)=2359808$
   bn1：$2\times 512=1024$
   bn2：$2\times 512=1024$
   conv3：$(256\times 512\times 1\times 1+512)=131584$（因为输入通道数和输出通道数不同，需要 conv3）
   两个 Residual_block 的总参数量：$(1180160+2359808+1024+1024+131584)\times 2=7471872$
8. 自适应平均池化层 adv_pool
   nn.AdaptiveAvgPool2d(1)
   参数量：$0$（池化层没有可学习的参数）
9. 全连接层 fc
   nn.Linear(512, 1000)
   参数量：$(512\times 1000+1000)=513000$
   总参数量
   将所有层的参数量相加：
   $9472+128+0+148672+460352+1838592+7471872+0+513000=10442088$
   因此，MyResNet18 模型的参数量为 $10,442,088$。