从零开始构建大模型第三步：损失函数优化器余弦退火调度器

昨天我们已经搭建好了transformer的骨架，有了一个数据流动的容器，接下来我们开始第三阶段：训练基础设施
需要手写训练所需的组件，而不是直接调用库函数：
Cross-Entropy Loss: 手写交叉熵损失函数，注意处理 LogSumExp 的数值稳定性 。
AdamW 优化器: 手写 AdamW 优化算法，包括动量更新和权重衰减逻辑。
学习率调度:实现 Cosine Annealing（余弦退火）学习率调度器，带 Warmup 阶段 。
Checkpointing:实现模型和优化器状态的保存与加载 。
Data Loader: 实现高效的数据加载器，使用 `np.memmap` 处理无法一次性读入内存的大文件 。

1.交叉熵损失

1. 什么是交叉熵损失？

在语言模型中，我们的目标是预测下一个 token。对于每一个位置，模型输出的是一个未归一化的数值向量（Logits），我们需要将其转化为概率，并计算目标单词的概率有多大。

公式通常分为两步：

1.Softmax: 将 Logits 转化为概率 。

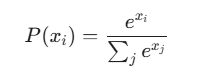
2.Negative Log Likelihood (NLL): 计算真实目标 target 的负对数概率。

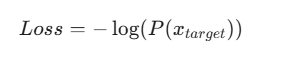
将两步合并，就得到了 Cross-Entropy Loss 的最终公式：

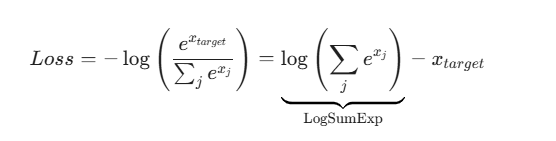
2. 为什么要处理数值稳定性？

看上面公式中的 。

如果 很大（例如 1000）， 会在计算机中直接变成 （上溢出），导致 Loss 变成 NaN。

如果 很小（例如 -1000），会变成 0（下溢出），导致分母为 0。

3. LogSumExp Trick (核心技巧)

为了解决这个问题，利用数学恒等式：

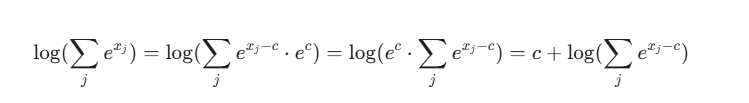
通常取 。

这样做的好处：

• 指数部分变成了 。

• 最大值的项变成了 。

• 其他项都是负数，指数结果在 之间。

• 彻底消除了上溢出问题，且保证了分母至少为 1（不会除以 0）。

PyTorch 代码实现

下面我将从零手写一个带有数值稳定性处理的 Cross-Entropy Loss，并将其与 PyTorch 官方的实现进行对比验证。

import torch
import torch.nn.functional as F

def manual_cross_entropy(logits, target):
    """
    手写 Cross Entropy Loss，包含 LogSumExp 技巧。
    
    Args:
        logits: 模型的原始输出，形状为 (batch_size, vocab_size)
        target: 真实的标签索引，形状为 (batch_size,)
    
    Returns:
        loss: 标量损失值
    """
    
    # --- 步骤 1: LogSumExp (数值稳定性处理) ---
    
    # 1.1 找到每一行的最大值 c
    # keepdim=True 是为了保持形状为 (batch_size, 1)，方便后续广播计算
    c, _ = torch.max(logits, dim=1, keepdim=True)
    
    # 1.2 将 logits 减去最大值，防止 exp 溢出
    logits_shifted = logits - c
    
    # 1.3 计算 exp
    exp_logits = torch.exp(logits_shifted)
    
    # 1.4 求和
    sum_exp = torch.sum(exp_logits, dim=1, keepdim=True)
    
    # 1.5 取对数，并加回 c
    # log_sum_exp 的形状是 (batch_size, 1)
    log_sum_exp = torch.log(sum_exp) + c
    
    # --- 步骤 2: 获取目标 target 对应的 logits ---
    
    # 我们需要从 logits 中取出 target 索引对应的那个值。
    # logits 形状: (B, V), target 形状: (B)
    # gather 需要 index 和 input 维度一致，所以先把 target 变成 (B, 1)
    target_logits = logits.gather(dim=1, index=target.unsqueeze(1))
    
    # --- 步骤 3: 计算 Loss ---
    
    # 公式: Loss = LogSumExp - x_target
    # 此时 loss_per_sample 形状为 (batch_size, 1)
    loss_per_sample = log_sum_exp - target_logits
    
    # --- 步骤 4: 求平均 ---
    return loss_per_sample.mean()

# ================= 验证环节 =================

# 模拟数据：Batch size = 2, Vocab size = 5
batch_size = 2
vocab_size = 5

# 随机生成 logits (模拟模型输出)
fake_logits = torch.randn(batch_size, vocab_size, requires_grad=True)
# 随机生成 target (模拟真实标签)
fake_target = torch.randint(0, vocab_size, (batch_size,))

print(f"Logits:\n{fake_logits}")
print(f"Target indices: {fake_target}")

# 1. 调用我们手写的函数
my_loss = manual_cross_entropy(fake_logits, fake_target)
print(f"\n我的 Loss: {my_loss.item():.6f}")

# 2. 调用 PyTorch 官方函数
# PyTorch 的 CrossEntropyLoss 内部自动做了 LogSoftmax + NLLLoss，也处理了数值稳定性
torch_loss = F.cross_entropy(fake_logits, fake_target)
print(f"官方 Loss: {torch_loss.item():.6f}")

# 3. 检查是否一致
assert torch.allclose(my_loss, torch_loss), "报错：两者结果不一致！"
print("\n✅ 验证通过。")

2.Adamw优化器：

1. 为什么我们需要 AdamW？

我们都知道，在标准的随机梯度下降（SGD）中，L2 正则化（在损失函数中加 ）和权重衰减（在更新参数时减去 ）在数学上是等价的。

但是在 Adam 中，它们不等价。

• Adam 的问题：Adam 会根据梯度的二阶矩（，即梯度的平方）来调整每个参数的学习率。如果你使用 L2 正则化，正则项的梯度会被加入到 中，然后被放入 和 中计算。这意味着，正则化的力度会被 Adam 的自适应学习率“扭曲”。参数的梯度越大，正则化力度反而越小，这与 L2 正则化的初衷（抑制过大的权重）相悖。

• AdamW 的解决：Decoupled Weight Decay（解耦权重衰减）。AdamW 将权重衰减从梯度更新的过程中剥离出来。它照常计算 Adam 的动量和自适应步长，但在最后更新参数的一瞬间，直接对参数进行一次衰减。

2. AdamW 的数学公式

这是我们需要实现的目标逻辑：

1. 梯度计算：

2. 动量更新 (1st Moment)：

3. 二阶矩更新 (2nd Moment)：

4. 偏差修正 (Bias Correction)：

   

   

5. 参数更新 (核心区别)：

   

注意公式最后一部分： 是直接加在更新项里的（或者说直接从权重中减去），并没有除以 。这就是解耦。

手写 PyTorch 实现 AdamW

import torch
from torch.optim import Optimizer
import math

class MyAdamW(Optimizer):
    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=1e-2):
        """
        初始化 AdamW 优化器
        
        Args:
            params: 待优化的参数 (通常是 model.parameters())
            lr: 学习率 (Learning Rate, 也就是公式中的 eta)
            betas: 包含两个系数的元组 (beta1, beta2)，用于控制动量和二阶矩的衰减
            eps: 一个极小值，防止分母为 0
            weight_decay: 权重衰减系数 (lambda)
        """
        # 1. 检查参数合法性 (这也是 PyTorch 源码的标准做法)
        if not 0.0 <= lr:
            raise ValueError(f"Invalid learning rate: {lr}")
        if not 0.0 <= eps:
            raise ValueError(f"Invalid epsilon value: {eps}")
        if not 0.0 <= betas[0] < 1.0:
            raise ValueError(f"Invalid beta parameter at index 0: {betas[0]}")
        if not 0.0 <= betas[1] < 1.0:
            raise ValueError(f"Invalid beta parameter at index 1: {betas[1]}")
        if not 0.0 <= weight_decay:
            raise ValueError(f"Invalid weight_decay value: {weight_decay}")

        # 2. 将超参数打包成一个字典，称为 'defaults'
        defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay)
        
        # 3. 调用父类 Optimizer 的初始化
        # 这步操作会将 params 分组管理，虽然我们通常只有一个组
        super(MyAdamW, self).__init__(params, defaults)

这是优化器最关键的方法。每次调用 optimizer.step() 时，就会执行这里的代码。

请仔细看每一行注释，我将动量更新和权重衰减的逻辑完全拆解了。

def step(self, closure=None):
        """
        执行一步参数更新
        """
        loss = None
        if closure is not None:
            loss = closure()

        # 遍历每一个参数组 (param_group)
        # 大多数情况下，你只有一个组，包含了模型的所有参数
        for group in self.param_groups:
            
            # 获取该组的超参数
            beta1, beta2 = group['betas']
            weight_decay = group['weight_decay']
            lr = group['lr']
            eps = group['eps']

            # 遍历该组中的每一个参数 (parameter)
            for p in group['params']:
                # 如果参数没有梯度 (grad is None)，则跳过
                if p.grad is None:
                    continue
                
                # 获取当前的梯度数据
                grad = p.grad.data
                
                # --- 状态管理 (State) ---
                # 优化器需要记住上一步的动量(m)和二阶矩(v)，这些存储在 self.state 中
                state = self.state[p]

                # 如果是第一次运行 (step 0)，需要初始化 m 和 v 为全 0 张量
                if len(state) == 0:
                    state['step'] = 0
                    # m_0: 指数移动平均的梯度 (Momentum)
                    state['exp_avg'] = torch.zeros_like(p.data)
                    # v_0: 指数移动平均的梯度平方 (Variance)
                    state['exp_avg_sq'] = torch.zeros_like(p.data)

                # 取出 m 和 v
                exp_avg = state['exp_avg']
                exp_avg_sq = state['exp_avg_sq']
                
                state['step'] += 1
                
                # --- 逻辑 1: 权重衰减 (Weight Decay) 的解耦实现 ---
                # 在 AdamW 中，权重衰减通常先于梯度更新执行，或者独立执行。
                # 公式: theta = theta - lr * lambda * theta
                if weight_decay != 0:
                    # p.data.mul_(scalar) 是原地乘法操作
                    p.data.mul_(1 - lr * weight_decay)

                # --- 逻辑 2: 更新动量 (Momentum / 1st Moment) ---
                # 公式: m_t = beta1 * m_{t-1} + (1 - beta1) * g_t
                exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)

                # --- 逻辑 3: 更新二阶矩 (Variance / 2nd Moment) ---
                # 公式: v_t = beta2 * v_{t-1} + (1 - beta2) * (g_t ^ 2)
                # addcmul_ 意味着: output = output + alpha * (tensor1 * tensor2)
                exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)

                # --- 逻辑 4: 偏差修正 (Bias Correction) ---
                # 因为 m 和 v 初始化为 0，在初期会偏向 0，需要放大回来
                bias_correction1 = 1 - beta1 ** state['step']
                bias_correction2 = 1 - beta2 ** state['step']
                
                # 计算分母: sqrt(v_t_hat) + eps
                # 这里为了计算效率，我们直接操作数值
                # 真实的 step size = lr / bias_correction1
                step_size = lr / bias_correction1
                
                denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(eps)

                # --- 逻辑 5: 参数更新 ---
                # 公式: theta = theta - step_size * (m_t / denom)
                # 注意：这里的 theta 已经是被 Weight Decay 衰减过的了
                p.data.addcdiv_(exp_avg, denom, value=-step_size)

        return loss

3.学习率调度

需要设计一种策略，让模型在训练初期先缓慢“热身”（Warmup），然后把学习率提高，接着随着训练的进行，用一种像余弦波浪一样的曲线（Cosine Annealing）慢慢降低学习率，直到训练结束。

一、 什么是学习率调度 (Learning Rate Scheduling)？

想象你在山上（初始状态），你的目标是下到山谷的最低点（损失函数 Loss 最小的地方）。“学习率”就是你下山时迈出的步长。

• 如果不调度（固定学习率）：

  • 步子太大：你可能会直接跨过最低点，在山谷两边反复横跳，永远下不去（无法收敛）。

  • 步子太小：你走得太慢，天黑了还没走到山脚（训练时间过长，或者卡在半山腰的小坑里）。

• 学习率调度：

  • 这就是根据时间调整你的步长。通常的策略是：刚开始步子大一点以便快速下山，越接近谷底，步子越小，以便精准地停在最低点。

二、 什么是 Warmup + Cosine Annealing？

这种策略是目前训练大模型（如 Transformer, BERT, GPT）和许多计算机视觉模型的标配。它结合了两个阶段：

1. Warmup 阶段（热身）

• 动作： 在训练开始的前几轮（Epoch），学习率从 0慢慢线性增加到预设的 最大学习率。

• 为什么要这样做？

  • 模型刚开始训练时，参数是随机初始化的，对数据一无所知。

  • 这时候如果学习率太大（步子迈太大），模型会根据第一批数据剧烈震荡，导致参数乱飞，甚至直接导致训练崩溃（NaN）。

  • Warmup 就像运动员热身，先让模型慢慢适应数据，稳定下来。

2. Cosine Annealing 阶段（余弦退火）

• 动作： 热身结束后，学习率开始下降。但不是像下楼梯一样突然下降，而是沿着 余弦函数（Cosine Function） 的曲线，平滑、缓慢地下降到 0（或一个极小值）。

• 为什么要这样做？

  • 余弦曲线在刚开始下降时比较慢，中间快，最后又变慢。

  • 这种平滑的下降方式通常能比阶梯式下降（Step Decay）找到更好的模型参数，因为它保留了较高的学习率更长时间，有机会跳出局部的坏坑（Local Minima）。

我们将使用 PyTorch 来实现这个功能。为了方便你理解，我使用了 PyTorch 官方推荐的组合方式：LinearLR (用于 Warmup) + CosineAnnealingLR (用于退火)，并通过 SequentialLR 把它们串联起来。

import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import LinearLR, CosineAnnealingLR, SequentialLR
import matplotlib.pyplot as plt

# 1. 设置一些基本参数
# -------------------------
initial_lr = 0.1      # 我们的目标最大学习率
total_epochs = 100    # 总共训练多少轮
warmup_epochs = 10    # 前10轮用于热身

# 2. 创建一个虚拟模型和优化器
# -------------------------
# 我们这里不需要真的训练模型，只需要优化器来模拟学习率的变化
model = nn.Linear(10, 1) 
optimizer = optim.SGD(model.parameters(), lr=initial_lr)

# 3. 定义调度器 (Schedulers)
# -------------------------

# 阶段 A: Warmup 调度器
# start_factor=0.01 表示从 0.01 * initial_lr 开始
# end_factor=1.0 表示结束时达到 1.0 * initial_lr
# total_iters=warmup_epochs 表示这个过程持续多少轮
scheduler_warmup = LinearLR(
    optimizer, 
    start_factor=0.01, 
    end_factor=1.0, 
    total_iters=warmup_epochs
)

# 阶段 B: Cosine Annealing 调度器
# T_max 是退火阶段的长度（总轮数 - 热身轮数）
# eta_min 是最后降到的最低学习率（通常为0）
scheduler_cosine = CosineAnnealingLR(
    optimizer, 
    T_max=total_epochs - warmup_epochs, 
    eta_min=0
)

# 阶段 C: 把它们串联起来
# milestones=[warmup_epochs] 意思是：到了第10轮，就从 Warmup 切换到 Cosine
scheduler = SequentialLR(
    optimizer, 
    schedulers=[scheduler_warmup, scheduler_cosine], 
    milestones=[warmup_epochs]
)

# 4. 模拟训练过程并记录学习率
# -------------------------
lrs = [] # 用来保存每一轮的学习率，方便画图

print("开始模拟训练...")
for epoch in range(total_epochs):
    # 获取当前的学习率
    current_lr = optimizer.param_groups[0]['lr']
    lrs.append(current_lr)
    
    # 模拟一步优化器更新 (optimizer.step)
    # 在真实代码中，这里会有 loss.backward()
    optimizer.step()
    
    # 更新学习率 (这是关键！每轮结束都要调用)
    scheduler.step()

print("模拟结束。")

# 5. 可视化 (如果运行这段代码，你会看到一条曲线)
# -------------------------
# 这是一个上升再下降的曲线
plt.figure(figsize=(10, 5))
plt.plot(lrs, label='Learning Rate')
plt.title('Cosine Annealing with Warmup')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.axvline(x=warmup_epochs, color='r', linestyle='--', label='End of Warmup') # 画一条红线标记热身结束
plt.legend()
plt.grid(True)
plt.show()

4.Checkpointing（检查点机制）

一、 核心概念：我们需要存什么？

新手往往以为只需要保存“模型参数”（Model Weights）。但这是一个误区。如果你想完美地“断点续传”，你需要保存整个训练现场的信息。

这就好比你存档游戏时，不仅要保存角色的属性（模型参数），还要保存角色的位置（训练轮数）、背包里的道具（优化器状态）等。

通常我们需要在一个 Python 字典（Dictionary）里打包以下内容：

1. model_state_dict: 模型的参数（权重和偏置）。

2. optimizer_state_dict: (非常重要) 优化器的状态。

   • 为什么？ 还记得我们刚才学的“动量”吗？优化器会记住之前的梯度方向。如果你不存这个，恢复训练时优化器就会“失忆”，导致训练曲线剧烈波动。

3. scheduler_state_dict: (非常重要) 学习率调度器的状态。

   • 为什么？ 如果你用了 Cosine Annealing，不存这个，恢复训练时学习率会重置回初始的大数值，破坏已经收敛的模型。

4. epoch: 当前训练到了第几轮（为了知道从哪里继续）。

5. loss: 当前的损失值（用于记录和对比）。

我们将实现两个核心函数：save_checkpoint（存档）和 load_checkpoint（读档）。

import torch
import torch.nn as nn
import torch.optim as optim
import os # 用于处理文件路径

# 定义一个简单的玩具模型
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.fc = nn.Linear(10, 1)

    def forward(self, x):
        return self.fc(x)

# 初始化组件
model = SimpleModel()
optimizer = optim.Adam(model.parameters(), lr=0.001)

这个函数负责把内存里的状态打包，写入硬盘。

def save_checkpoint(state, filename="my_checkpoint.pth.tar"):
    """
    保存检查点
    :param state: 一个字典，包含模型、优化器等所有状态
    :param filename: 保存的文件名，通常以 .pth 或 .pt 结尾
    """
    print("=> 正在保存 Checkpoint...")
    torch.save(state, filename)
    print(f"=> 保存成功: {filename}")

# --- 模拟使用场景 ---
# 假设现在是第 5 轮训练结束
current_epoch = 5
current_loss = 0.35

# 打包我们需要保存的所有东西
checkpoint = {
    "state_dict": model.state_dict(),             # 模型参数
    "optimizer": optimizer.state_dict(),          # 优化器记忆
    "epoch": current_epoch,                       # 当前轮数
    "loss": current_loss                          # 当前Loss
}

# 调用函数保存
save_checkpoint(checkpoint)

这个函数负责从硬盘读取文件，并把状态恢复到模型和优化器中。

def load_checkpoint(checkpoint_file, model, optimizer):
    """
    加载检查点
    :param checkpoint_file: 存档文件的路径
    :param model: 需要恢复的模型实例
    :param optimizer: 需要恢复的优化器实例
    :return: 恢复后的起始轮数 (start_epoch)
    """
    print(f"=> 正在加载 Checkpoint: {checkpoint_file} ...")
    
    # 1. 加载文件到内存
    # map_location='cpu' 意思是如果之前是用GPU存的，现在强制加载到CPU上（防止报错）
    # 如果你在GPU上跑，可以去掉 map_location
    checkpoint = torch.load(checkpoint_file, map_location='cpu')
    
    # 2. 恢复模型参数
    model.load_state_dict(checkpoint["state_dict"])
    
    # 3. 恢复优化器状态 (这就恢复了动量等信息)
    optimizer.load_state_dict(checkpoint["optimizer"])
    
    # 4. 获取之前的轮数，以便我们要知道从第几轮开始继续
    start_epoch = checkpoint["epoch"] + 1 
    
    # 5. 获取之前的 loss (可选，用于打印)
    previous_loss = checkpoint["loss"]
    
    print(f"=> 加载完成！将从第 {start_epoch} 轮继续训练 (上次 Loss: {previous_loss})")
    
    return start_epoch

# --- 模拟：程序重新启动了 ---

# 1. 重新实例化全新的模型和优化器 (此时它们是初始状态，什么都没学到)
new_model = SimpleModel()
new_optimizer = optim.Adam(new_model.parameters(), lr=0.001)

# 2. 尝试加载存档
checkpoint_path = "my_checkpoint.pth.tar"
start_epoch = 0 # 默认从0开始

# 检查文件是否存在
if os.path.exists(checkpoint_path):
    # 如果存在存档，就覆盖当前的模型和优化器，并更新 start_epoch
    start_epoch = load_checkpoint(checkpoint_path, new_model, new_optimizer)
else:
    print("=> 没有发现存档，从头开始训练")

# 3. 继续训练循环
total_epochs = 10
print(f"\n开始训练循环，从 Epoch {start_epoch} 到 {total_epochs}")

for epoch in range(start_epoch, total_epochs):
    # ... 这里执行你的训练代码 (Forward, Backward, Step) ...
    print(f"正在训练 Epoch {epoch} ...")
    
    # 假设每轮结束我们都存一次档
    # 这样如果程序在 Epoch 7 崩溃，下次就能从 Epoch 7 继续
    checkpoint = {
        "state_dict": new_model.state_dict(),
        "optimizer": new_optimizer.state_dict(),
        "epoch": epoch,
        "loss": 0.123 # 假装这是当前的loss
    }
    save_checkpoint(checkpoint)

5.data loader

核心概念：什么是 np.memmap？

把它想象成一个“滑动窗口”。

• 普通读取：把你家里的所有书（数据）都搬到书桌（内存）上。如果书太多，桌子就塌了。

• 内存映射：书还是放在书架（硬盘）上。你只把你需要读的那一页（数据片段）拿到了桌子上。

下面我将分步实现一个基于 PyTorch 的高效数据加载器。

第一步：准备模拟数据

为了演示，我们先创建一个比较大的二进制文件保存在硬盘上。

import numpy as np
import os

# 1. 定义文件名和数据大小
filename = 'large_dataset.bin'
num_samples = 10000     # 假设有 1万 个样本
feature_dim = 256       # 每个样本有 256 个特征
dtype = 'float32'       # 数据类型

# 2. 生成一些随机数据
print(f"正在生成数据: {num_samples} x {feature_dim} ...")
data = np.random.randn(num_samples, feature_dim).astype(dtype)

# 3. 将数据写入硬盘 (使用 memmap 的写入模式 'w+')
# 这里我们创建一个内存映射文件，用来写入数据
fp = np.memmap(filename, dtype=dtype, mode='w+', shape=(num_samples, feature_dim))
fp[:] = data[:]  # 将内存中的随机数据写入硬盘映射区
fp.flush()       # 确保数据写入磁盘

# 删除内存中的 data 变量，模拟我们现在只有硬盘上的文件
del data, fp
print(f"文件 '{filename}' 已创建完毕。")

第二步：实现 Dataset 类 (核心部分)

这是最关键的一步。我们将继承 PyTorch 的 Dataset 类，并使用 np.memmap 以只读模式打开文件。

import torch
from torch.utils.data import Dataset

class MemmapDataset(Dataset):
    def __init__(self, filename, shape, dtype='float32'):
        """
        初始化函数：在这里我们只建立映射，不加载数据。
        """
        self.filename = filename
        self.shape = shape
        self.dtype = dtype
        
        # 关键点：使用 mode='r' (只读模式)
        # 这行代码几乎瞬间完成，因为它只是建立了文件和内存的链接，
        # 并没有真正把几百 GB 的数据读进来。
        self.data = np.memmap(
            self.filename, 
            dtype=self.dtype, 
            mode='r', 
            shape=self.shape
        )

    def __len__(self):
        """
        告诉 PyTorch 数据集一共有多少个样本。
        """
        # shape[0] 是样本数量 (10000)
        return self.shape[0]

    def __getitem__(self, index):
        """
        获取单个样本：只有在这里，数据才真正从硬盘被读取到内存。
        """
        # 1. 从 memmap 中切片读取一行数据
        # 这一步就像在普通的 numpy 数组中取值一样简单
        sample = self.data[index]
        
        # 2. 将 numpy 数组转换为 PyTorch 张量 (Tensor)
        # 为了避免数据拷贝，通常 copy=True 比较安全，但这里为了演示直接转换
        tensor_sample = torch.from_numpy(sample)
        
        return tensor_sample

第三步：使用 DataLoader 加载数据

现在我们有了 Dataset，接下来用 DataLoader 来进行批量读取、打乱顺序等操作。

from torch.utils.data import DataLoader

# 1. 实例化我们的数据集
# 注意：在实际项目中，你需要知道数据的 shape。
# 通常我们会把 shape 信息单独存在一个元数据文件(json/txt)里。
dataset = MemmapDataset(
    filename='large_dataset.bin', 
    shape=(10000, 256), 
    dtype='float32'
)

# 2. 创建 DataLoader
# batch_size=32: 每次训练给模型喂 32 个样本
# shuffle=True:  每个 epoch 开始时打乱数据顺序
# num_workers=2: 使用 2 个子进程并行加载数据 (加速读取)
dataloader = DataLoader(
    dataset, 
    batch_size=32, 
    shuffle=True, 
    num_workers=2
)

# 3. 模拟训练循环
print("开始模拟训练循环...")

for i, batch in enumerate(dataloader):
    # batch 是一个形状为 [32, 256] 的 Tensor
    # 在这里，数据已经从硬盘读入内存，并被整理成了 Batch
    
    # [此处可以是你的模型前向传播代码]
    # output = model(batch)
    
    if i < 3: # 只打印前3个batch演示一下
        print(f"Batch {i}: 形状 {batch.shape}, 数据类型 {batch.dtype}")
    else:
        break

print("演示结束。")

# 清理生成的临时文件
import os
try:
    # 关闭 memmap 对象以释放文件句柄
    del dataset.data 
    os.remove('large_dataset.bin')
    print("临时文件已清理。")
except PermissionError:
    print("无法删除文件，可能仍被占用。")

为什么这样做最高效？

1. 极低的内存占用：哪怕文件有 1TB，你的 Python 进程可能只占用了几百 MB 内存（仅包含当前的 Batch 数据）。

2. 操作系统级优化：np.memmap 利用了操作系统的虚拟内存机制（Virtual Memory）。如果你的 RAM 还有空闲，操作系统会自动把频繁读取的硬盘数据缓存到 RAM 里（Page Cache），下次读取会飞快。

3. 支持并行：配合 DataLoader 的 num_workers，可以让 CPU 在训练模型的同时，预先从硬盘把下一批数据读取好。