算法基础教学：哈希表

深入理解哈希表原理与实现

最新推荐文章于 2025-12-09 19:50:25 发布

原创最新推荐文章于 2025-12-09 19:50:25 发布 · 829 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #散列表 #数据结构

算法初级教学专栏收录该内容

6 篇文章

订阅专栏

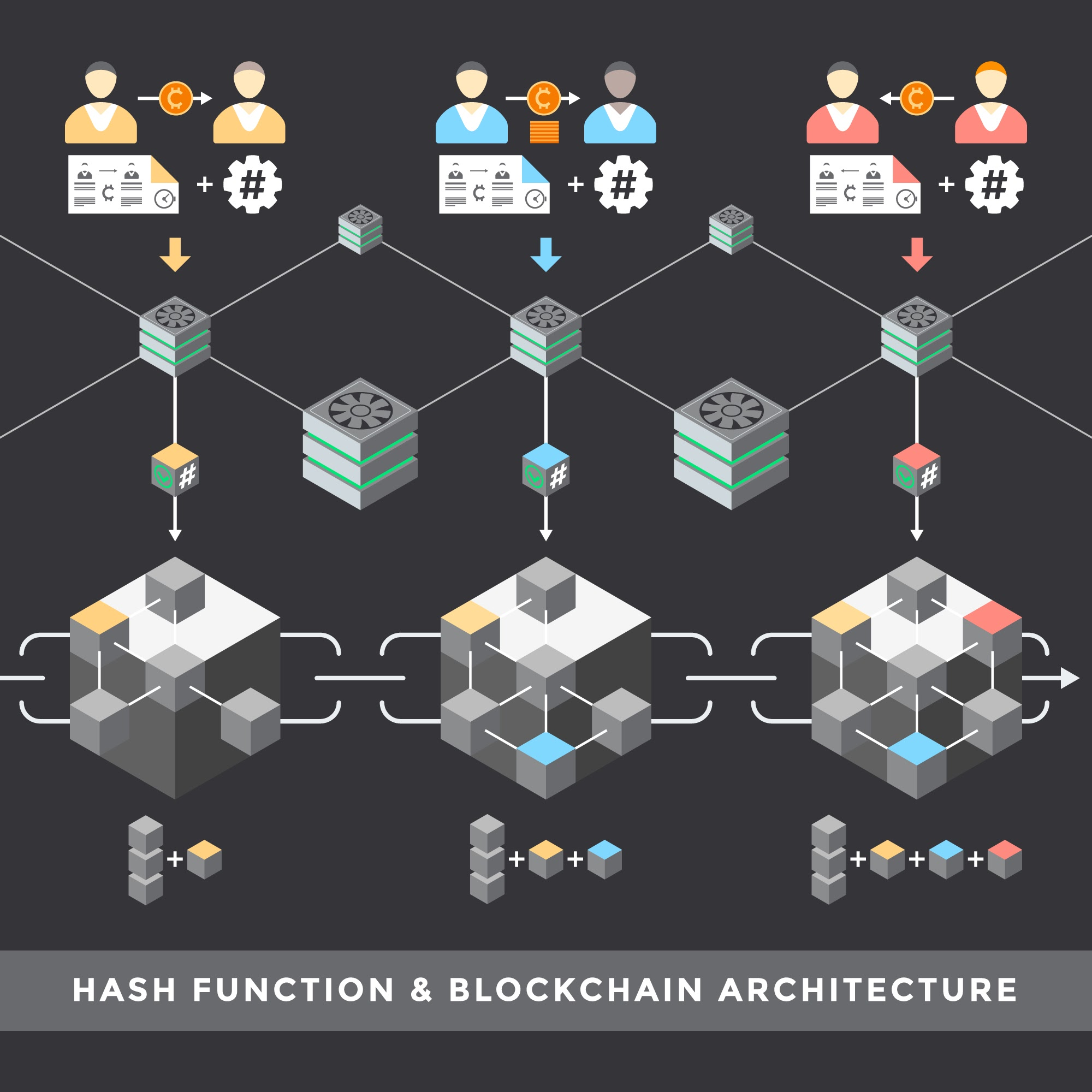
第一部分：哈希的起源

1. 计算机硬件的“物理特权”：数组 (Array)

要理解哈希表，我们必须先看一眼你的内存条（RAM）。

在计算机底层，内存是一块巨大的、线性的存储空间。你可以把它想象成一条无限长的街道，每个房子都有一个唯一的门牌号（内存地址，Memory Address）。

CPU 有一个物理特权：随机访问（Random Access）。

只要你给 CPU 一个内存地址（比如 0x00A1），它就能用 O(1)的时间瞬间由硬件电路直接定位并取出数据。它不需要像链表那样从头遍历。

这就是为什么数组（Array） 如此之快。

数组在内存中是连续存放的。
如果你知道数组的起始地址 Start，你想访问第 i个元素，CPU 只需要做一次简单的加法运算
算出地址后，直接去取。这就是 O(1)的物理本质。

2. 完美的理想：直接寻址表 (Direct Addressing)

假设我们现在要存储这一届研究生的数据。如果学号是连续的整数：0, 1, 2, 3 ... 100。我们根本不需要哈希表，直接申请一个长度为 101 的数组 Student[101]。

查学号为 5 的人？直接访问 Student[5]。
速度：光速。

但现实很骨感，我们面临两个问题：

数据稀疏（浪费内存）： 如果学号是 20250001 到 20259999，中间只有 50 个人。为了存这 50 个人，你要申请一个长度一千万的数组吗？内存会爆炸。

键值非整数（CPU 听不懂）： 如果我想存的名字是字符串 "Alice"，或者是一个复杂的 Object。内存地址必须是整数，CPU 不知道 "Alice" 是第几个格子。

3. 哈希表的诞生：一种“映射”的魔法

为了解决上面两个问题，计算机科学家想出了一个绝妙的主意：

能不能搞一个“转换器”（函数），把世界上万事万物（字符串、图片、很大的数字），都“映射”成一个比较小的、数组能容纳的下标范围？

这个转换器，就是 哈希函数 (Hash Function)。

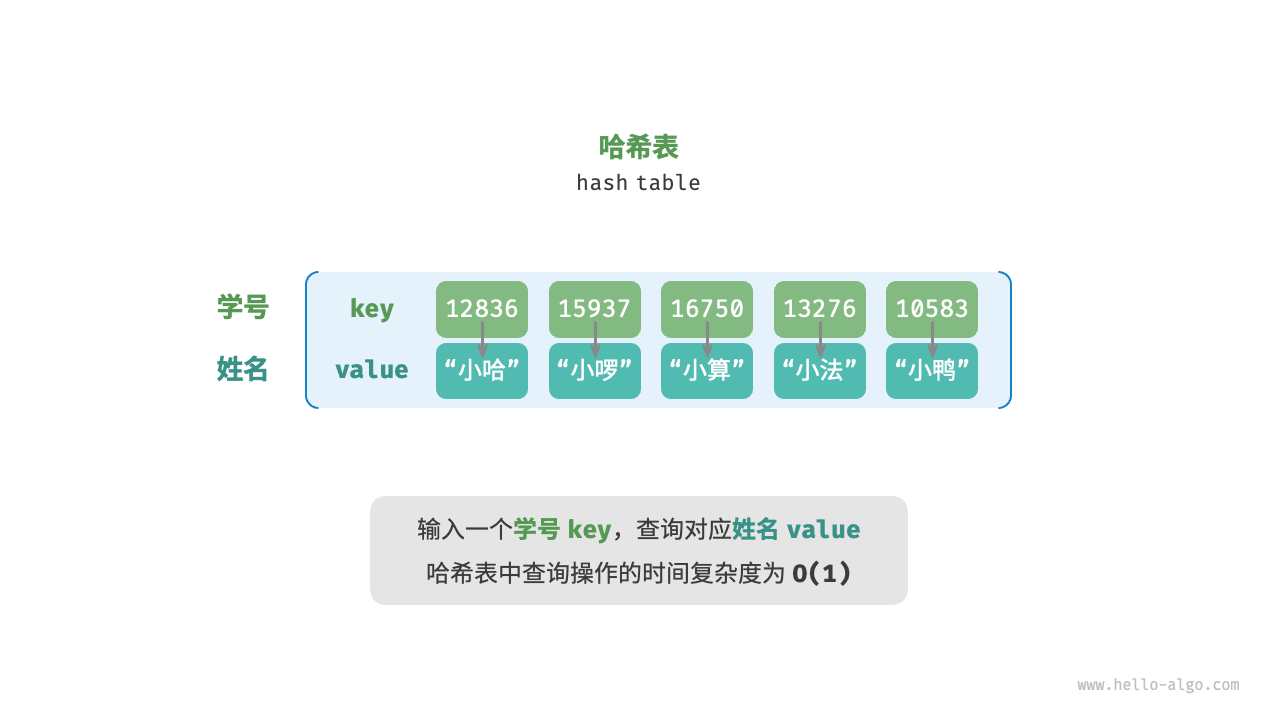
请看上图（或想象这个过程）：

输入 (Key)： 比如字符串 "Alice"。
黑盒处理 (Hash Function)：
- 计算机底层把 "Alice" 看作一串二进制数字（ASCII 码）。
- 通过某种复杂的数学运算（比如位运算、取模），把这串巨大的二进制数字，压缩变成一个小的整数。
- 假设算出来是 3。
落槽 (Buckets)： 我们申请一个较小的数组（比如长度为 8）。既然算出来是 3，我们就把 "Alice" 的数据扔进数组下标为 3 的格子里。

这就是哈希表的核心逻辑： 它本质上还是一个数组（为了利用 O(1) 的硬件特权），但它在外面包裹了一层“数学计算”，把人类逻辑中的 Key，强行翻译成了 CPU 能听懂的 Array Index。

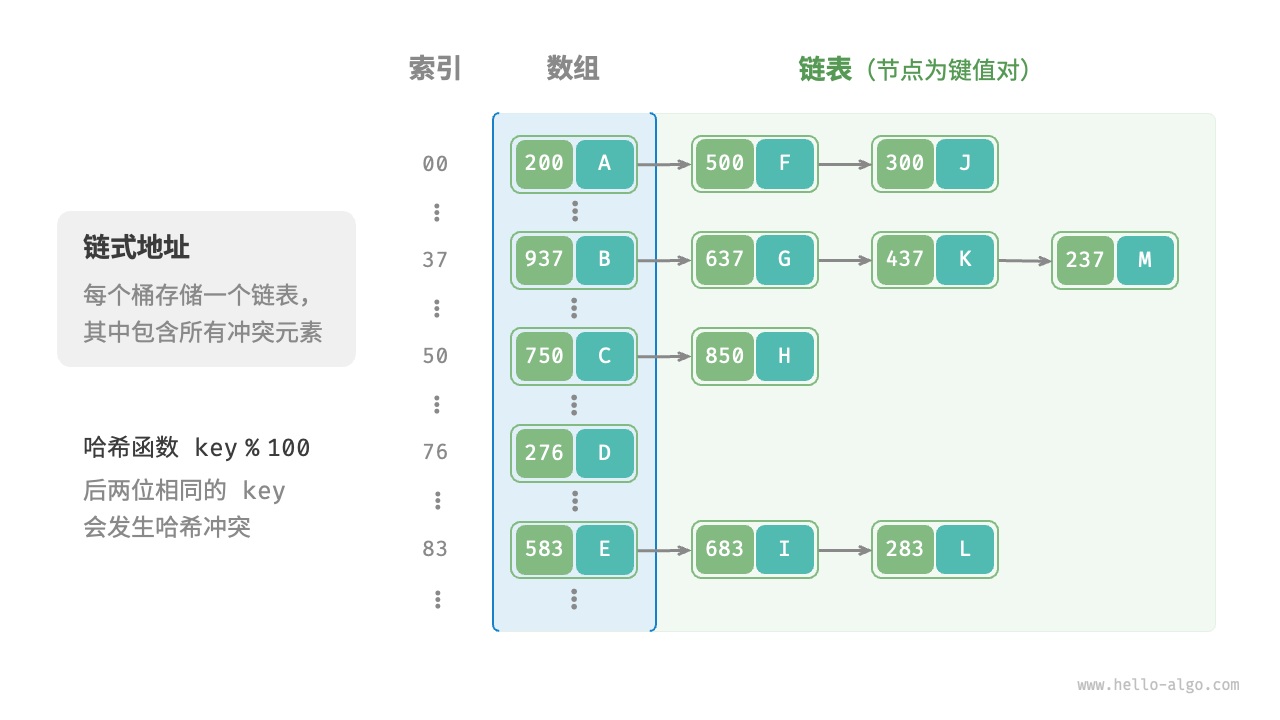
第二部分：哈希冲突

哈希冲突（Hash Collision）是所有哈希表实现中必须面对的“物理铁律”。

为什么？这就要提到数学上的抽屉原理（Pigeonhole Principle）：如果你有 10 个苹果（无限可能的输入 Key），但只有 9 个抽屉（有限的数组空间），那么必然有一个抽屉里至少装了两个苹果。

当 "Alice" 和 "Bob" 都要抢占数组下标 3 时，我们作为“上帝”（架构师），必须制定规则来平息这场战争。

在计算机底层，主要有两种经典的解决流派。这两种流派体现了完全不同的内存哲学。

1. 拉链法 (Separate Chaining)

这是最直观、也是教科书最常讲的方法。

底层逻辑： 我们不再把数组的每个格子看作是一个“座位”，而是把它看作一个“挂钩”（也就是一个指针 head pointer）。

场景： "Alice" 来了，算出 Hash 值为 3。
- 数组 Arr[3] 原本是空的（NULL）。
- 我们申请一块新内存存 "Alice"，把 Arr[3] 指向她。
冲突： "Bob" 来了，算出 Hash 值也是 3。
- CPU 发现 Arr[3] 已经挂着 "Alice" 了。
- 没关系，我们使用链表 (Linked List) 的逻辑。我们在 "Alice" 后面再申请一块内存存 "Bob"，让 "Alice" 的 next 指针指向 "Bob"。

优点： 逻辑简单，永远不会填满（只要内存够，链表可以无限长）。
缺点（关键）： 对 CPU 缓存（Cache）非常不友好。
- 链表的节点在物理内存中是“散落”的。
- 当你遍历这个链表查找 "Bob" 时，CPU 必须在内存中跳来跳去（Pointer Chasing），这会导致大量的 Cache Miss。对于追求极致性能的系统，这很致命。

2. 开放寻址法 (Open Addressing)

这是 Python 的 dict（早期版本）和许多高性能系统偏爱的方式。

底层逻辑： 数组的每个格子只能存一个数据。绝不使用额外的链表。

场景： "Alice" 占了下标 3。
冲突： "Bob" 来了，算出也是 3。
- CPU 发现 3 被占了。
- 线性探测 (Linear Probing)： 那我去看看下标 4 有没有人？如果 4 也没人，我就坐这儿。
- 如果 4 还有人，我就看 5……以此类推，直到找到一个空位。

优点： 极度利用 CPU 缓存。
- 因为数据都存放在同一个大数组里，物理内存是连续的。
- 当 CPU 读取下标 3 时，它会顺便把 4、5、6 也加载到 L1/L2 缓存中（利用局部性原理）。如果是线性探测，查找速度会非常快。
缺点： 团块效应 (Clustering)。
- 如果你运气不好，数据都挤在了一块，查找一个人可能要从 3 一直走到 100。这会让 O(1) 的理想直接退化成 O(n)。

性能的隐患：O(1) 只是理想

你可能在想：“不是说哈希表是 O(1) 吗？”

这是哈希表的平均情况。

在最坏的情况下（Worst Case），比如所有人的 Hash 值都算出来是 3：

拉链法： 变成了一个超长的链表。
开放寻址法： 变成了从头走到尾的线性扫描。

这时候，查询速度退化为 O(n)。这在网络安全中甚至是一种攻击方式（Hash Collision DoS Attack），黑客故意构造大量产生相同 Hash 值的请求，把服务器 CPU 跑死。

第三部分：扩容 (Rehashing)

现在我们知道了如何存数据，也知道了如何解决冲突。但还有一个更可怕的问题在等着我们。

想象一下，你申请了一个长度为 8 的数组。如果你一直在往里面塞数据，用开放寻址法，很快 8 个位置就满了。用拉链法，虽然能存，但每个挂钩下面的链表都变得巨长无比，查询越来越慢。

这就引出了第三部分： 当房间太拥挤时，哈希表如何进行一次惊心动魄的“搬家”——扩容（Rehashing）？这是工程实现中最耗时、最容易导致系统卡顿的环节。

1. 警戒线：装载因子 (Load Factor)

哈希表怎么知道自己“太挤了”？

我们引入一个概念：装载因子 (Load Factor, $\alpha$ )。

$\alpha = \frac{\text{now}}{\text{len}}$

如果数组长度是 10，里面装了 7 个元素， $\alpha = 0.7$ 。
在工业界（比如 Java 的 HashMap 或 Python 的 dict），通常把警戒线设定在 0.75 (3/4) 左右。
一旦 $\alpha$ 超过 0.75，哈希表就会判定：“现在的冲突概率太高了，必须扩容！”

2. 为什么不能直接“把房子变大”？

这是初学者最容易误解的地方。你可能会想：“如果数组满了，我在后面追加一段内存不就行了吗？”

不行。 这会进行一次全员大迁徙。

底层原因： 还记得我们是怎么算出元素位置的吗？通常是取模运算：

$Index = Hash(Key) \pmod{Size}$

注意那个 Size（数组长度）。

搬家前： 假设 Size = 8。Key "Alice" 的 Hash 是 11。 $11 \pmod 8 = 3$ 。它住在 3 号房。
搬家后： 我们把数组扩大两倍，Size = 16。
问题来了： $11 \pmod{16} = 11$ 。

看到了吗？

当数组长度改变时，几乎所有元素原本的居住地址（下标）都失效了！ "Alice" 必须从 3 号房搬到 11 号房。

这意味着： 扩容时，计算机必须遍历旧数组里的每一个元素，重新计算它们的 Hash 值，重新取模，重新寻找新数组里的位置。

这是一个 O(n)的重型操作。如果你的哈希表里有 10 亿个数据，这次扩容可能会让你的程序突然“卡顿”好几秒。这也是为什么在高性能计算中，如果我们预先知道数据量，一定要预分配（Pre-allocate） 足够大的空间，避免中间发生扩容。

进阶：Python 的 `dict` 到底是怎么实现的？

紧凑哈希表”（Compact Dict）

在老版本的 Python（和大多数传统哈希表）中，哈希表是一个稀疏的大数组：

老版本结构 (稀疏):
Index 0: [ NULL ]
Index 1: [ Hash | Key | Value ]
Index 2: [ NULL ]  <-- 浪费空间
Index 3: [ Hash | Key | Value ]
...

Python 3.6+ 把它拆成了两个数组：

索引数组 (Indices)： 一个只存整数的小数组（非常紧凑）。
实体数组 (Entries)： 一个存具体数据的数组（按插入顺序紧密排列）。

工作流程：

当你要存 "Alice" 时，算出 Hash 对应下标 3。
Python 不直接把 Alice 存在 Indices[3] 里。
它把 Alice 的数据（Key/Value）追加到 实体数组 的末尾（比如是第 0 个存进来的）。
然后在 Indices[3] 里记下一个数字：0。意思是“去实体数组的第 0 个位置找数据”。

这样做的好处（非常硬核）：

省内存： Indices 数组只存简单的整数（int8 或 int32），空位再多也不占多少地。而真正的重头数据 Entries 是紧密排列的，没有空隙。
保留插入顺序： 这就是为什么 Python 3.7+ 官方宣布 dict 是有序的！因为 Entries 数组是按时间顺序往后追加的。