从零开始构建大模型第二步：优化版transformer架构搭建

原创于 2025-11-28 13:38:16 发布 · 1k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#transformer #深度学习 #人工智能 #机器学习 #神经网络 #语言模型 #nlp

从零开始一步步构建大模型专栏收录该内容

12 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

昨天已经构建好了分词器，今天进入我们的第二部分:

手写优化版本的 Transformer 架构

这是最核心的部分。你不能使用 `torch.nn.Linear`, `torch.nn.LayerNorm`, `torch.nn.MultiheadAttention` 等

必须继承 `nn.Module` 并手写前向传播逻辑。
需要逐个实现以下模块：
1. Linear 层: 实现 y = Wx，注意权重初始化。

2. Embedding 层:实现 token ID 到向量的查找表。

3. RMSNorm: 实现 Root Mean Square Layer Normalization（Llama 用的归一化方式）。

4. SwiGLU 前馈网络: 实现带门控机制的激活函数（SiLU + GLU），这是现代 LLM 的标配。

5. RoPE (旋转位置编码): 实现 Rotary Positional Embeddings，这比绝对位置编码更先进。

6. 多头注意力 (Attention):实现 Masked Multi-Head Self-Attention。需要手动处理 Q, K, V 的投

影、缩放点积、因果遮罩以及 Softmax 的数值稳定性。

7. Transformer Block & LM: 将上述组件组装成完整的 Transformer 模块和语言模型。

这一章节会非常长，我们不仅要会写代码，回顾知识点，当然我不会再深入的讲基础知识，仅仅做个回顾和深化，但我们不满足简单的定理，以及我会问一些及其深刻的问题，作为一个小点收尾，我敢打包票的事，你用一周或者两周时间吃透这篇博客，你的能力会有质的飞跃。

第一步：从零开始实现线性层

1. 什么是线性层？ (直觉理解)

在神经网络中，线性层（也叫全连接层或 Dense 层）就像是一个变换器。

输入：一堆数字（比如一个 512 维的向量，代表“苹果”这个词的特征）。
作用：它通过矩阵乘法，把这堆数字“揉捏、拉伸、旋转”，变换成另一组维度的数字。
目的：
- 改变维度：比如把 512 维的特征压缩成 64 维（降维），或者扩展到 2048 维（升维）。
- 信息融合：它让输入向量里的每一个数字都参与运算，混合出新的特征。

2. 数学原理

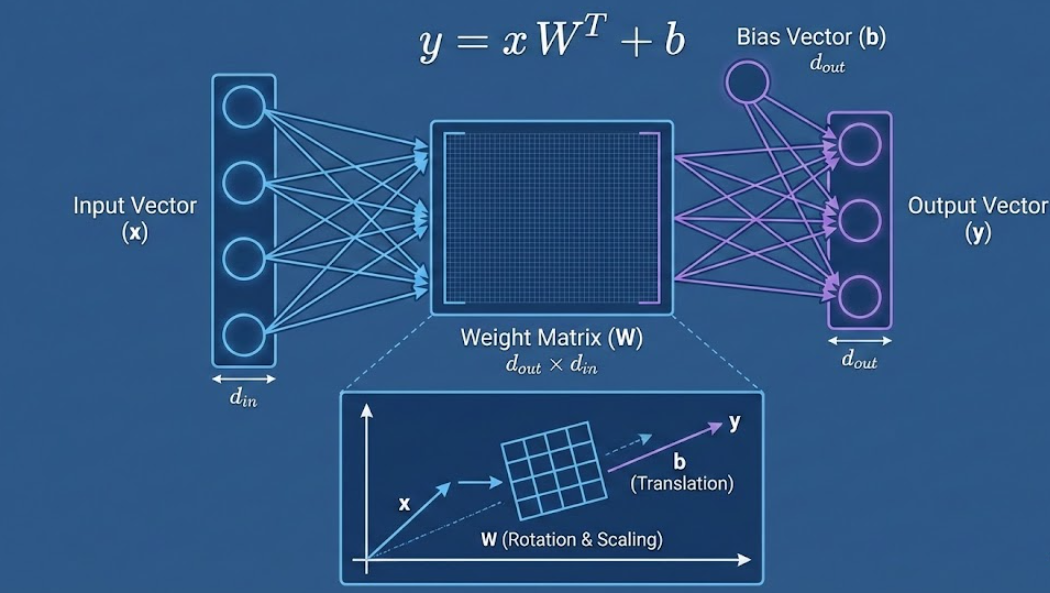
线性层的核心公式非常简单，就是初中/高中数学的直线方程 $y = ax + b$ 的矩阵版本：

$y = x W^T + b$

其中：

$x$ (Input): 输入向量（或者矩阵）。
$W$ (Weight): 权重矩阵。这是模型要学习的“参数”。它决定了如何“翻译”输入。
$b$ (Bias): 偏置向量。这也是参数。它决定了输出结果的基础偏移量（就像直线的截距）。
$y$ (Output): 输出结果。

注意形状 (Shape) 的小细节：

在 PyTorch 的 nn.Linear 标准实现中，为了计算效率，权重矩阵 W$的形状通常存储为 [out_features, in_features]。

所以在前向传播时，我们需要把W转置（Transpose，即 $W^T$ ）或者直接用 $x$ 乘以 $W$ 的转置，这就变成了矩阵乘法。

import torch
import torch.nn as nn
import math

class MyLinear(nn.Module):
    def __init__(self, in_features, out_features, bias=True):
        """
        初始化线性层。
        
        Args:
            in_features (int): 输入向量的维度大小。
            out_features (int): 输出向量的维度大小。
            bias (bool): 是否使用偏置项 (b)。
        """
        super().__init__() # 必须调用父类的初始化，这是 PyTorch 的规矩
        
        self.in_features = in_features
        self.out_features = out_features
        
        # --- 1. 定义权重 W ---
        # 我们使用 nn.Parameter 来包装 Tensor。
        # 只有被 nn.Parameter 包装过的 Tensor，PyTorch 才会把它当作"模型参数"，
        # 在 model.parameters() 中才能看到它，优化器才会去更新它。
        # 形状通常是 [输出维度, 输入维度]
        self.weight = nn.Parameter(torch.Tensor(out_features, in_features))
        
        # --- 2. 定义偏置 b ---
        if bias:
            # 偏置的形状就是输出的维度 [out_features]
            self.bias = nn.Parameter(torch.Tensor(out_features))
        else:
            # 如果不需要偏置，就设为 None
            self.register_parameter('bias', None)

        # --- 3. 权重初始化 (非常重要！) ---
        # 如果不初始化，Tensor 里是内存中的随机垃圾值，模型根本无法训练（会梯度爆炸或消失）。
        # 这里我们模拟 PyTorch 默认的 Kaiming Uniform 或 Xavier 初始化。
        # 简单来说：我们需要把权重限制在一个很小的范围内，比如 [-k, k]。
        self.reset_parameters()

    def reset_parameters(self):
        """
        初始化权重的数值。
        为了让训练稳定，权重的方差通常需要和输入维度的平方根成反比。
        """
        # 这是一个经验公式，用于保证一开始输出的数值不会太大也不会太小
        k = 1.0 / math.sqrt(self.in_features) 
        
        # 使用均匀分布初始化权重 W，范围在 [-k, k] 之间
        nn.init.uniform_(self.weight, -k, k)
        
        # 同样初始化偏置 b
        if self.bias is not None:
            nn.init.uniform_(self.bias, -k, k)

    def forward(self, input):
        """
        前向传播逻辑：y = x @ W.T + b
        
        Args:
            input (Tensor): 输入数据，形状通常是 [Batch_Size, Sequence_Length, in_features]
        
        Returns:
            output (Tensor): 输出数据，形状是 [Batch_Size, Sequence_Length, out_features]
        """
        # --- 核心计算步骤 ---
        
        # 1. 矩阵乘法
        # input 的最后一位是 in_features
        # self.weight 的形状是 [out_features, in_features]
        # 为了能相乘，我们需要把 weight 转置变成 [in_features, out_features]
        # input @ weight.T  <-- '@' 是矩阵乘法符号
        output = input @ self.weight.t()
        
        # 2. 加上偏置
        if self.bias is not None:
            output = output + self.bias
            
        return output

提问：

问题 1：为什么线性层可以被视为一种“空间变换器”？如果去掉激活函数，堆叠 100 层线性层会发生什么？

答：

1.坐标系的旋转与缩放：

矩阵 $W$ 其实定义了一组新的“基底”（Basis）。当你做 $x @ W^T$ 时，你实际上是把输入向量 $x$ 投影到了 $W$ 定义的新坐标系中。

如果 $W$ 是正交矩阵，它就是旋转（不改变向量长度）。
如果 $W$ 是对角矩阵，它就是缩放（拉伸或压缩轴）。
核心直觉：线性层在试图找到一个“更好”的视角来观察数据。比如，在一个乱成一团的数据堆里，线性层试图旋转一下视角，让不同类别的数据在空间中分得更开。

2.恐怖的“秩塌陷”（Rank Collapse）：

如果你在两个线性层之间不加非线性激活函数（如 ReLU, SiLU），那么：

$y = (x W_1) W_2 = x (W_1 W_2) = x W_{new}$

无论你堆叠多少层，它们最终都能在数学上合并成仅仅一层矩阵。这意味着，100 层纯线性网络的能力 $\equiv$ 1 层线性网络。

深层含义：深度学习的本质力量来自于非线性（把纸揉皱再展开），线性层只是负责在每次非线性变换前，把数据调整到最适合被“切分”的位置。

问题 2：在 Transformer 的 FFN（前馈网络）中，线性层通常是“升维”再“降维”（比如从 d 到 4d 再回到 d）。为什么要多此一举？这里发生了什么？

这是目前大模型可解释性研究（Mechanistic Interpretability）最前沿的话题之一（参考 Anthropic 的 "Superposition" 论文）。

答：

1.Cover 定理 (Cover's Theorem)：

低维空间中纠缠在一起、无法线性区分的数据（比如“苹果”既是水果又是科技公司），投射到高维空间后，往往变得线性可分。

第一层 Linear $d \to 4d$ ：把原本挤在一起的概念“撒开”。在 4096 维的空间里，“苹果(水果)”和“苹果(公司)”可能挤在一起；但在 16384 维的空间里，模型可以把它们拉得很远，分别处理。

2.多义性与叠加 (Polysemanticity & Superposition)：

神经网络中的神经元往往是“多义”的。一个神经元可能同时响应“猫”和“汽车”。

线性层的升维操作，是为了解开这些叠加态。
你可以把 FFN 中的第一个 Linear 层看作是模式匹配器。W 中的每一行都是一个“模版”（Key）。输入 x与这些模版做点积，激活值越大，说明 x 越像这个模版。
第二个 Linear 层则是重组器，把检测到的特征重新组合回原本的维度流向下一层。

问题 3：为什么我们刚才在代码里初始化权重时，要用 1/sqrt(in_features)？如果我把它改成常数 0.01 或者 100 会怎样？

这涉及到了信号传播理论 (Signal Propagation) 和 等距性 (Isometry)，是训练超深网络（如 100+ 层的 LLM）不崩溃的关键。

答：

1.方差守恒 (Variance Preservation)：

想象一下，输入 $x$ 的方差是 1。

经过 $y = \sum w_i x_i$ 运算后，如果 $w$ 和 $x$ 都是独立的随机变量， $y$ 的方差大约是 $n \times Var(w) \times Var(x)$ （ $n$ 是输入维度）。

如果 $Var(w)$ 不除以 $n$ （即 $\frac{1}{\sqrt{n}}$ 的平方），输出的方差就会放大 $n$ 倍。
经过 10 层，方差放大 $n^{10}$ 倍 $\to$ 数值爆炸（NaN）。
如果初始化太小，经过 10 层，方差 $\to$ 0 $\to$ 信号消失（模型学不到东西）。

最优秀的架构设计，是让数据流过 100 层网络后，其模长（Norm）和方差依然保持稳定，既不爆炸也不消失。

第二步，从零实现embedding层

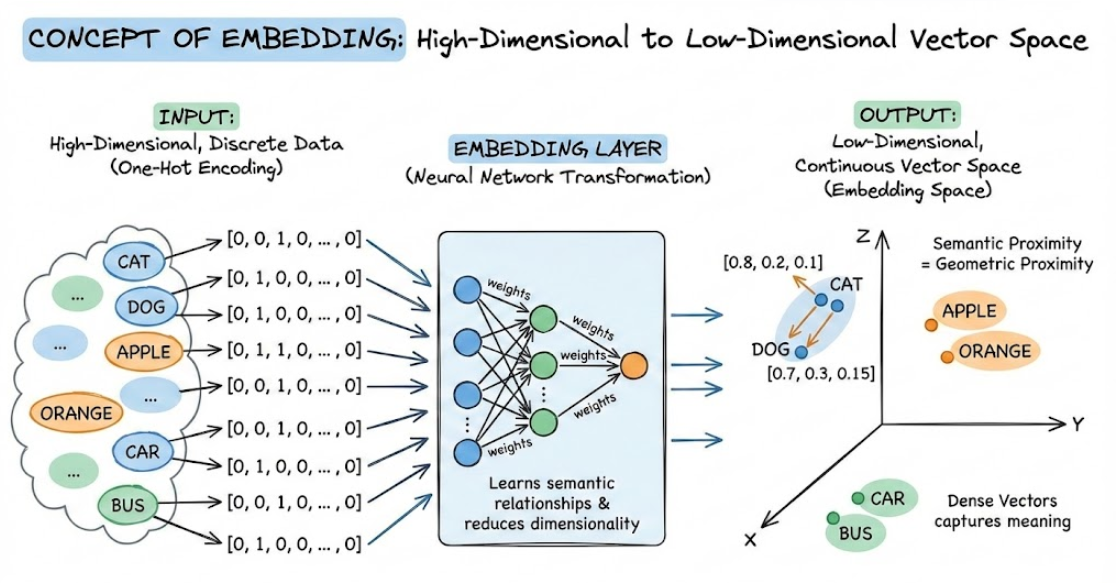
用最直白的话来说，Embedding 层就是一座“桥梁”。它负责把人类能理解的离散符号（比如单词的 ID），转换成计算机神经网络能高效处理的连续向量。

1. 直观理解：从“编号”到“特征”

假设我们词表里有“苹果”这个词，它的 Token ID 是 5。

输入（ID）：5。这只是一个数字，对神经网络来说，5 和 6 只差 1，但“苹果(5)”和“香蕉(6)”的意思可能很近，而“苹果(5)”和“汽车(100)”的意思很远。单纯的数字无法体现这种语义关系。
Embedding 层的作用：它把 5 变成一串浮点数，比如 [0.8, -0.1, 0.5, ...]。
- 这串数字代表了“苹果”在数学空间里的特征（比如：是红色的吗？是食物吗？是圆的吗？）。
- 经过训练后，语义相近的词，它们对应的向量在空间距离上也会很近。

2. 核心实现机制：查找表 (Lookup Table)

在代码实现层面，Embedding 层其实就是一个巨大的、可训练的矩阵。

矩阵的形状： $V \times D$
- $V$ (Vocab Size)：词表大小（例如 Llama 3 是 128k，一般小模型可能是 30k-50k）。
- $D$ (Embedding Dimension)：每个词向量的长度（例如 512, 768, 4096）。
操作逻辑：

当输入一个 Token ID 为 $i$ 时，Embedding 层所做的，仅仅是取出这个矩阵的第 $i$ 行。

注意：虽然在数学上，这等同于用一个 One-Hot 向量去乘以这个矩阵，但在计算机工程实现（PyTorch）中，为了速度，我们直接做数组索引（Array Indexing）。

假设词表大小 $V=4$ ，维度 $D=3$ ：

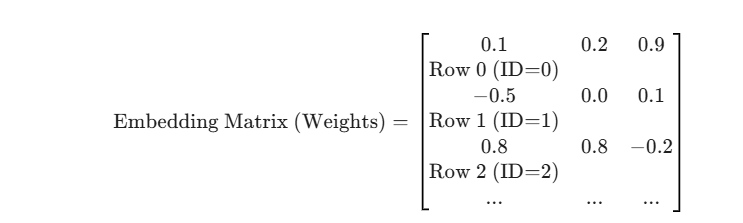
在原始的《Attention Is All You Need》论文中，Embedding 输出后，需要乘以 $\sqrt{d_{model}}$ 。

原因：Embedding 初始化后的数值通常比较小（方差为 1 或更小），而后续的位置编码（Positional Encoding）数值在 -1 到 1 之间。为了不让语义信息被位置信息“淹没”，通常会放大 Embedding 的数值。

Embedding 层就是一个形状为 [vocab_size, d_model] 的可训练矩阵（查找表）。

输入：一堆整数索引 [Batch, Length]。
动作：根据索引“查表”。
输出：一堆稠密向量 [Batch, Length, Dim]。

class MyEmbedding(nn.Module):
    def __init__(self, vocab_size, d_model):
        """
        手动实现嵌入层。
        vocab_size: 词表大小 (行数)
        d_model: 嵌入维度 (列数)
        """
        super().__init__()
        self.vocab_size = vocab_size
        self.d_model = d_model

        # 这是一个巨大的查找表
        self.weight = nn.Parameter(torch.Tensor(vocab_size, d_model))

        # 初始化：通常使用正态分布
        self.reset_parameters()

    def reset_parameters(self):
        # 标准正态分布初始化
        nn.init.normal_(self.weight, mean=0.0, std=1.0)

    def forward(self, x):
        """
        x: Token IDs, Shape (Batch, Seq_Len), 例如 [[1, 5], [2, 9]]
        """
        # 手动查表
        # PyTorch 的 tensor 支持高级索引
        # self.weight[x] 会自动根据 x 里的 ID，去 weight 里把对应的行“扣”出来
        # 并保持 x 的形状结构

        return self.weight[x]

提问：

1.在标准的反向传播（Backpropagation）中，Embedding 层（作为查找表）的梯度更新与普通的全连接层（Dense/Linear Layer）有什么本质区别？这种区别决定了我们在训练 Transformer 时，为什么通常偏好 Adam/AdamW 优化器，而不是标准的 SGD（即使带 Momentum）？

考察点： 你是否理解 Lookup Table 操作在数学上导致了梯度的稀疏性。

2.在 Transformer 中，我们将 Word Embedding 和 Positional Embedding 直接相加（Element-wise Sum），然后送入下一层。为什么是相加而不是拼接（Concatenation）？既然相加了，位置信息和语义信息混在一起，模型怎么区分哪个是“词的含义”，哪个是“位置”？请利用高维空间的近似正交性（Almost Orthogonality in High Dimensions）来解释。

考察点： 你是否具备高维空间的几何直觉。这是很多初学者最困惑的地方——“加在一起不就乱了吗？”

3.在理想情况下，我们将词映射到向量空间，希望它们均匀分布（Isotropy），充分利用空间容量。但研究发现，训练好的 LLM Embedding 往往呈现严重的各向异性（Anisotropy）——即所有词向量都挤在一个狭窄的圆锥（Cone）里。请从 Softmax 损失函数（Cross Entropy Loss）的角度推导，为什么模型会倾向于把 Embedding 推向同一个方向？

考察点： 这是前沿研究级别的问题。考察你对 Loss Function 如何塑造 Latent Space 的理解。

场景模拟：

假设训练一个模型，词表里有两个词：

常用词：“的” (ID: 1)，出现了 10,000 次。
生僻词：“熵” (ID: 999)，只出现了 1 次。

SGD 的视角（一视同仁）：

SGD 的更新公式是 $w = w - \eta \cdot \nabla w$ 。

对于“的”，它更新了 10,000 次，参数调整得很完美。
对于“熵”，它只在某一个 Batch 里更新了 1 次。
问题来了：因为 SGD 用的是全局统一的学习率 $\eta$ ，对于“熵”来说，这一次更新可能太微不足道了，还没来得及走到正确的位置，训练就结束了。

Adam 的视角（自适应）：

Adam 会为每个参数维护一个“二阶动量”（可以理解为该参数历史梯度的方差/活跃度）。

Adam 发现 Embedding 矩阵第 1 行（“的”）经常动，所以它会保持正常的更新步长。
Adam 发现 Embedding 矩阵第 999 行（“熵”）几百年不动一次（稀疏性）。
神来之笔：Adam 会对自己说：“这个 ID:999 好不容易出现一次，它的梯度历史方差很小，说明它是稀疏特征，我要放大这次更新的步长，让它学快点”

结论：

Embedding 层本质上是稀疏更新的（一个 Batch 只更新一小部分行）。Adam 能够自动为那些“生僻词”提供更大的更新力度，这对于自然语言处理（长尾分布）至关重要。这就是为什么 Transformer 几乎标配 Adam/AdamW。

为什么“语义”+“位置”不会混成一锅粥？

这确实反直觉。在二维平面上，$(1,0)$ 加上 $(0,1)$ 变成了 $(1,1)$，既不像 X 也不像 Y，混了。

但在高维空间（比如 4096 维），有一个数学定理叫 “高维空间的近似正交性”。

直觉模拟：

想象你在一个巨大的球面上随机插两根针。

在 2 维圆上，这两根针很容易重合或方向相近。
在 1000 维球面上，你随机选两个方向，计算它们的点积，你会发现几乎总是接近 0。也就是说，在高维空间随便抓两个向量，它们大概率是相互垂直（正交）的。

“加法”的真相：

$\text{Input} = \text{Word\_Emb} + \text{Pos\_Emb}$

因为维度足够高， $D=4096$ ：

Word Embedding 占据了一个子空间。
Positional Embedding 占据了另一个几乎垂直的子空间。
虽然它们数值加在一起了，但并没有发生严重的“干涉”。

后续层怎么区分？

后续的 Linear 层（比如 $W_Q, W_K, W_V$ ）只是一个矩阵乘法。矩阵乘法可以看作是旋转和缩放。

模型可以学习一个 $W$ 矩阵，把它投影到“语义轴”上，这时候位置信息就被抵消了。
模型也可以学习另一个 $W$ 矩阵，把它投影到“位置轴”上，提取位置信息。

结论：

加法是最高效的信息融合方式。如果不加，而是拼接（Concat），维度会翻倍（计算量翻4倍）。因为高维空间足够空旷，我们才敢直接把它们叠在一起，模型能够毫不费力地把它们拆分开。

Embedding 的“锥形坍缩”这是一个关于 Loss 函数如何“作弊”的故事。

目标： 我们用 Softmax 预测下一个词。公式核心包含 $e^{x \cdot w_y}$ 。为了降低 Loss，模型希望正确单词的 Logits ( $x \cdot w_y$ ) 尽可能大。

点积公式：

$A \cdot B = \|A\| \|B\| \cos(\theta)$

要让点积变大，模型有两个选择：

正道：调整方向 $\theta$ ，让 $A$ 和 $B$ 语义对齐（ $\cos \theta \to 1$ ）。这是我们想要的。
邪道（作弊）：无脑增大模长 $\|A\|$ 和 $\|B\|$ 。不管方向对不对，只要向量够长，点积就很大。

为什么会坍缩成一个锥形？

在训练语料中，有些词（如 "the", "is", ","）出现频率极高。
为了让整体 Loss 最小，模型发现一个偷懒的办法：把所有词向量都推向同一个方向（通常是那些高频词的方向），并且把模长拉得很长。
这样一来，随便拿两个词算点积，值都很大，模型觉得“我很棒”。
后果：所有词向量都挤在一个狭窄的圆锥里（各向异性），这极大地浪费了高维空间的表达能力（本来应该均匀分布在球面上）。

结论： 这就是为什么后来的模型（如 BERT, Llama）经常需要 LayerNorm（强制把模长拉回正常水平）或者在推理时做一些修正。这也解释了为什么如果你直接计算原生 Embedding 的 Cosine 相似度，很多完全不相关的词相似度也会很高——因为它们都指向同一个角落。

第三步，从零实现RMSNorm归一化

RMSNorm (Root Mean Square Layer Normalization) 是一种用于神经网络（特别是 Transformer）的归一化技术。

简单来说，它是经典的 Layer Normalization (LayerNorm) 的简化版和加速版。目前最流行的开源大模型（如 Llama 系列、Gemma、PaLM）几乎都放弃了 LayerNorm 而选择了 RMSNorm。

1. 核心直觉：只要“缩放”，不要“平移”

要理解 RMSNorm，得先看它的前辈 LayerNorm 做了什么。LayerNorm 为了让数据分布稳定，做了两件事：

Re-centering (去中心化/平移)： 减去均值（Mean），让数据中心对齐到 0。
Re-scaling (重缩放)： 除以标准差（Std），让数据的发散程度（方差）归一化。

RMSNorm 的作者发现了一个事： 在 Transformer 的训练中，LayerNorm 带来的收益（加速收敛、稳定训练），绝大部分来自于 Re-scaling (重缩放)，而 Re-centering (减均值) 并没有带来多少实质性的帮助，反而浪费了计算资源。

RMSNorm 的逻辑是：

“既然减均值没用，那我就不减了。我只保留缩放功能，根据输入的均方根 (RMS) 来把数据强行拉回到一个标准的尺度。”

2. 数学原理对比

假设我们有一个输入向量 $\mathbf{x}$ ，包含 $d$ 个元素。

传统 LayerNorm 的步骤：

计算均值 $\mu$ 。
计算方差 $\sigma^2$ (基于与均值的差)。
归一化： $\hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}}$
仿射变换 (Learnable parameters)：乘以缩放因子 $\gamma$ 并加上偏置 $\beta$ 。

$y = \hat{x} \cdot \gamma + \beta$

RMSNorm 的步骤 (更简单)：

RMSNorm 假设均值为 0 (或者说不在乎均值)，直接计算均方根 (Root Mean Square)：

计算 RMS：

$\text{RMS}(\mathbf{x}) = \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2 + \epsilon}$

(注意：这里是直接对 x^2 求平均，不需要减去均值 $\mu$ )
归一化：

$\bar{x}_i = \frac{x_i}{\text{RMS}(\mathbf{x})}$
缩放 (Learnable parameters)：

$y_i = \bar{x}_i \cdot \gamma_i$

(注意：RMSNorm 通常没有偏置项 $\beta$ ，只有缩放权重 $\gamma$ )

3. 为什么现代 LLM (如 Llama) 都用它？

计算速度更快 (Less Overhead)：

少算了一个均值 $\mu$ ，少做了一次减法操作。虽然单层看起来微不足道，但在几十层、几千亿参数的大模型中，这能节省可观的计算开销。
效果相当甚至更好：

实验证明，去掉均值偏移并不影响 Transformer 的收敛速度和最终精度。
数值稳定性：

RMSNorm 在处理极深网络时，对梯度的缩放更加自然，有助于防止梯度爆炸或消失。
简单的线性缩放特性：

它具有线性缩放不变性（Scaling Invariance），这对于基于点积注意力的模型（Transformer）非常友好。

class MyRMSNorm(nn.Module):
    def __init__(self, d_model, eps=1e-5):
        """
        d_model: 输入向量的维度
        eps: 防止分母为 0 的极小值
        """
        super().__init__()
        self.eps = eps
        # 这里的 weight 就是公式里的 gamma (缩放参数)
        # 它是一个可学习的参数，让模型自己决定每一层的数据缩放比例
        self.weight = nn.Parameter(torch.ones(d_model))

    def forward(self, x):
        """
        x shape: (Batch, Seq_Len, d_model)
        """
        # 1. 计算均方值 (Mean Square)
        # x.pow(2) 是平方
        # mean(-1) 是在最后一个维度（d_model）求平均
        # keepdim=True 保持形状，方便后续广播计算
        mean_square = x.pow(2).mean(dim=-1, keepdim=True)

        # 2. 计算均方根的倒数 (Reciprocal Square Root)
        # rsqrt(y) 等价于 1 / sqrt(y)
        # 加 eps 是为了防止分母为 0
        rsqrt = torch.rsqrt(mean_square + self.eps)

        # 3. 归一化并缩放
        # 原始向量 * 倒数 * 缩放参数
        return x * rsqrt * self.weight

# 测试一下
# rms = MyRMSNorm(512)
# x = torch.randn(2, 10, 512)
# out = rms(x)
# print(out.shape) # (2, 10, 512)且数值分布更稳定
# 假设 MyLinear 已经在上面定义好了

提问：

1.RMSNorm 具有“尺度不变性 (Scale Invariance)”。即对于输入 $x$ 和任意标量 $\alpha > 0$ ，有 $\text{RMSNorm}(\alpha x) = \text{RMSNorm}(x)$ 。请问，这种特性在反向传播（Backpropagation）时，对权重矩阵 $W$ 的梯度有什么具体影响？它如何隐式地调节了“有效学习率”？

答：

这道题考察你是否理解 Normalization 技术为什么能加速训练的根本原因。

梯度的正交性与缩放：

设 Loss 为 L，输入为 x，权重为 w。由于前向传播是不变的（ $f(w) = f(\alpha w)$ ），根据链式法则，权重的梯度 $\nabla_w L$ 会表现出特殊的性质。

数学推导会告诉你：梯度的模长与权重的模长成反比。

$||\nabla_w L|| \propto \frac{1}{||w||}$

如果不加 Normalization，当 $w$ 变大时，输出变大，梯度往往也变大（导致梯度爆炸）。但在 RMSNorm 下，如果 $w$ 变大（例如变为 $2w$ ），输出不变，Error 不变，但为了抵消前向传播中 $2$ 倍的放大，反向传播回来的梯度反而会缩小为原来的 $1/2$ 。

隐式学习率调度 (Adaptive Learning Rate)：

如果你使用标准的 SGD 更新： $w_{t+1} = w_t - \eta \nabla L$ 。

结合上面的性质，当权重范数 $||w||$ 很大时，梯度 $||\nabla L||$ 会很小。这相当于实际上步长变小了。

权重小 -> 梯度大 -> 更新步子大 -> 快速逃离初始区域。
权重大 -> 梯度小 -> 更新步子小 -> 在局部极小值附近微调。

结论： RMSNorm（以及 LayerNorm）实际上为模型引入了一种自动的、基于参数模长的学习率衰减机制，这比手动调参 learning rate 更能适应不同层的参数分布。

在现代 LLM 训练中（例如 Llama 3），我们通常使用 BF16 (BFloat16) 或 FP16 进行混合精度训练。在实现 RMSNorm 的时候：

$\bar{x}_i = \frac{x_i}{\sqrt{\frac{1}{d} \sum x_j^2 + \epsilon}}$

，如果直接按照公式实现，会有什么潜在的数值风险？你应该如何在代码层面规避这个问题？

答：这道题考察你是否有大规模训练的实战意识。理论完美的公式在计算机里可能会炸。

下溢出与上溢出 (Underflow/Overflow)：

在 FP16/BF16 中，能表示的最大数值有限（FP16 大约是 65504）。

如果 $x_j$ 的值比较大（比如 100）， $x_j^2$ 就会变成 10000。如果 $d$ （hidden size）是 4096，累加和 $\sum x_j^2$ 极易超过 FP16 的上限，导致变为 inf（无穷大），归一化结果变成 0，训练崩塌。
反之，如果 $x_j$ 很小， $x_j^2$ 可能下溢出为 0。

解决方案：

在手写代码时，必须强制类型转换。

不管输入 x 是什么精度（FP16/BF16），在计算平方和（ $\sum x^2$ ）和均值时，必须先转为 FP32 (float32) 进行累加，算完开根号后，再转回 FP16/BF16 参与后续计算。

Q: RMSNorm 相比 LayerNorm，去掉了减去均值 $\mu$ 的操作（Re-centering），并且通常去掉了加性偏置 $\beta$ （Bias）。从表示能力（Representation Power）的角度看，这种简化是否限制了模型的能力？为什么在 Transformer 的深层网络中，"平移不变性"（Shift Invariance）似乎变得不那么重要了？

这道题考察你对 Transformer 内部数据流动的直觉。

高维空间的各向同性：

LayerNorm 强制把数据中心移到 0。RMSNorm 允许数据在空间中有偏移。

但在高维空间（High Dimension）中，绝大多数随机向量几乎都是正交的，且分布在超球面上。研究发现，LayerNorm 学习到的 $\mu$ (shift) 通常非常接近于 0，或者对后续的 Attention/FFN 影响极小。

Transformer 中的非线性主要来自 FeedForward (SwiGLU/GeLU) 和 Attention。

如果下一层是 Linear 层（ $y = Wx + b$ ），那么 Linear 自带的 bias $b$ 其实已经提供了平移能力。
如果下一层是 Softmax（Attention 中），由于 Softmax 是平移不变的 $\text{softmax}(x+c) = \text{softmax}(x)$ ，RMSNorm 中保留的任何公共偏移量（Common Shift）在 Attention score 计算中都会被抵消掉。

结论： 减均值操作在 Transformer 架构中是冗余的。去掉它不仅没损失表达能力，反而因为减少了强制约束（让数据可以自由地在原点附近漂移），可能让模型更容易找到简单的解，同时正如你所知，计算更快。

第四步，从零实现ROPE旋转位置编码

1. 核心直觉：为什么是“旋转”？

传统的问题

绝对位置编码 (Absolute): 给每个 token 加一个固定的向量（比如第 5 个位置的 embedding）。缺点是模型很难理解“第 1005 个词”和“第 1000 个词”的关系，与“第 5 个词”和“第 0 个词”的关系是一样的。它只记住了“我在哪里”，没记住“我离你多远”。
相对位置编码 (Relative): 直接在计算 Attention 分数时，加入一个表示距离的偏置项。效果好，但计算稍微麻烦，且难以利用缓存优化（KV Cache）。

RoPE 的天才想法

RoPE 说：我们不要去“加”一个位置信息，我们把词向量在空间里“转”一个角度。

想象一下：

Token A 在位置 0，向量方向不变。
Token B 在位置 1，向量逆时针转 10 度。
Token C 在位置 2，向量逆时针转 20 度。

当我们要计算 Token B 和 Token C 的关系（点积）时，关键来了：它们的夹角差了 10 度。 如果你看 Token A 和 Token B，它们的夹角也差了 10 度。

在向量点积中，数值大小很大程度上取决于夹角。通过旋转，RoPE 使得两个 Token 的 Attention 分数只取决于它们的相对距离（角度差），而与它们的绝对位置无关。

2. 数学原理（由简入繁）

为了理解，我们先只看向量中的 2 个维度（二维平面）。

假设我们有一个 Query 向量 $\mathbf{q}$ 和一个 Key 向量 $\mathbf{k}$ 。

在位置 $m$ 的 Query 向量，我们记为 $\mathbf{q}_m$ 。

在位置 $n$ 的 Key 向量，我们记为 $\mathbf{k}_n$ 。

RoPE 的操作：

我们将向量 $\mathbf{q}$ 乘以一个旋转矩阵，旋转的角度是 $m \cdot \theta$ （位置 $m$ 乘以基准角度 $\theta$ ）。

$\mathbf{q}'_m = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \end{pmatrix}$

同理，对 $\mathbf{k}$ 在位置 $n$ 进行旋转 $n \cdot \theta$ 。

Attention 的核心是计算 $Attention Score = \mathbf{q}^T \mathbf{k}$ 。当我们计算带旋转位置信息的 $\mathbf{q}'_m$ 和 $\mathbf{k}'_n$ 的点积时，根据三角恒等式，你会发现绝对位置 $m$ 和 $n$ 消失了，只剩下 $m-n$ ：

$\mathbf{q}'_m \cdot \mathbf{k}'_n = |\mathbf{q}| |\mathbf{k}| \cos((m - n)\theta)$

结论： 两个向量的相关性，只取决于它们隔了多远（ $m-n$ ），这就是我们梦寐以求的相对位置性质！并且它是通过给每个 token 赋予绝对的旋转角度自然获得的。

3. 拓展到多维 (d_model)

实际模型维度 $d$ 很大（比如 4096）。RoPE 的做法是：两两分组。

把 4096 维的向量切成 2048 对 $(x_0, x_1), (x_2, x_3), ..., (x_{d-2}, x_{d-1})$ 。

每一对都在自己的二维平面里旋转。

但是，每一对的旋转速度（频率 $\theta$ ）是不一样的！

第一对转得很快（捕捉局部信息）。
最后一对转得很慢（捕捉长距离信息）。

公式如下（ $\theta_i$ 是频率）：

$\theta_i = 10000^{-2i/d}$

这就是为什么代码里常看到 10000.0 这个底数。

实现 RoPE 时有几个坑要注意：

只对 Q 和 K 使用：Value 向量是不需要旋转位置编码的（虽然加上去也没大错，但标准做法是不加）。
KV Cache 的处理：当你实现推理生成（KV Cache）时，传入的 seq_len 只有 1（当前生成的那个词）。但是，它的位置索引 m 必须是它在整句话里的真实位置。
- 错误做法：每次都用位置 0 的旋转角度。
- 正确做法：如果你已经生成了 10 个词，现在的第 11 个词应该用位置索引 10 的旋转角度。
Head Dimension：RoPE 是作用在每个 Attention Head 的维度上的，而不是整个 d_model 上。比如 Llama 7B，d_model=4096，32 个头，那么 head_dim = 128。RoPE 是在 128 维上计算的。

总结 RoPE 的优越性

外推性 (Extrapolation)：因为它是基于旋转角度的，模型更容易泛化到比训练时更长的序列上（虽然不是无限的，但比绝对位置好太多）。
无需参数：它没有可学习的参数，纯数学计算，初始化简单。
衰减特性：随着相对距离 $m-n$ 变大，Attention 的相关性会自然衰减（震荡衰减），这符合语言模型的直觉（离得越远的词关系通常越弱）。

class MyRoPE(nn.Module):
    def __init__(self, dim, max_seq_len=2048, base=10000.0):
        super().__init__()
        
        self.dim = dim
        self.base = base
        inv_freq = 1.0 / (self.base ** (torch.arange(0, dim, 2).float() / dim))
        self.register_buffer("inv_freq", inv_freq)
        self.cached_cos = None
        self.cached_sin = None
        self._update_cache(max_seq_len)

    def _update_cache(self, seq_len):
        
        if self.cached_cos is None or seq_len > self.cached_cos.shape[1]:
            t = torch.arange(seq_len, device=self.inv_freq.device, dtype=self.inv_freq.dtype)
            freqs = torch.outer(t, self.inv_freq)
            emb = torch.cat((freqs, freqs), dim=-1)
            self.cached_cos = emb.cos()[None, :, None, :]
            self.cached_sin = emb.sin()[None, :, None, :]

    def forward(self, x, start_pos=0):
        """
        start_pos: 告诉 RoPE 当前输入是从句子的第几个词开始的
        """
        seq_len = x.shape[1]

        # 截取对应的 cos/sin
        # 比如 start_pos=10, seq_len=1
        # 我们就取 cached_cos[10 : 11] 这一行
        cos = self.cached_cos[:, start_pos: start_pos + seq_len, :, :].to(x.device)
        sin = self.cached_sin[:, start_pos: start_pos + seq_len, :, :].to(x.device)

        return self._apply_rotary_emb(x, cos, sin)

    # _apply_rotary_emb 和 _rotate_half 和之前一样
    def _apply_rotary_emb(self, x, cos, sin):
        return (x * cos) + (self._rotate_half(x) * sin)

    def _rotate_half(self, x):
        x1, x2 = x.chunk(2, dim=-1)
        return torch.cat((-x2, x1), dim=-1)

# --- 测试代码 ---
# dim = 64 (假设每个头的维度是 64)
# rope = MyRoPE(dim)
# q = torch.randn(2, 10, 8, 64) # (Batch, Seq, Heads, Dim)
# q_rotated = rope(q)
# print(f"原始形状: {q.shape}, 旋转后形状: {q_rotated.shape}")
# print("RoPE 应用成功！注意形状没有变化，但是数值包含了位置信息。")

提问：

1.我们知道 RoPE 的核心性质是： $\langle f(\mathbf{q}, m), f(\mathbf{k}, n) \rangle = g(\mathbf{q}, \mathbf{k}, m-n)$ 。

请证明：为什么必须是复数域上的“旋转”（或者说正交变换），才能在点积中仅保留相对位置信息？如果是“缩放”或者“平移”操作，能实现这个性质吗？

如果我们将位置编码改为 $f(\mathbf{x}, m) = \mathbf{x} + \mathbf{p}_m$ 加法，这在点积 Attention 中展开后会多出哪些项？这些项为什么阻碍了纯粹的“相对位置”感知？

RoPE 中的频率由 $\theta_i = b^{-2i/d}$ 定义（通常 $b=10000$ ）。

当我们需要将模型扩展到比训练长度更长的序列时（Length Extrapolation），原本的 RoPE 表现会迅速下降。

请从“频率”和“波长”的角度解释，为什么 RoPE 在未见过的长距离上会失效？

追问：如果你了解 NTK-Aware Scaled RoPE 或 YaRN（这些是 Llama 扩展上下文用到的技术），它们是通过“插值（Interpolation）”还是“外推（Extrapolation）”来解决这个问题的？为什么在高频维度（ $\theta$ 大）和低频维度（ $\theta$ 小）上，我们需要不同的处理策略？

在标准的 Transformer 中，RoPE 是作用在 $W_q \mathbf{x}$ 和 $W_k \mathbf{x}$ 之后的。

如果我们在 Linear 层之前就对输入 $\mathbf{x}$ 应用 RoPE（即先旋转，再投影），这在数学上等价吗？为什么？

追问：RoPE 是针对 1D 序列设计的。假设现在我们要处理 2D 图像（Vision Transformer），你需要给图像的 $(x, y)$ 坐标设计位置编码。如果你简单地将 RoPE 分别应用在 x 轴和 y 轴上，根据矩阵乘法的性质（非交换性），会有什么潜在问题？

答：

1.为什么必须是“旋转”？（加法 vs 乘法）

你的直觉可能在想：“如果直接加一个位置向量，好像也能区分位置啊？”

核心目标：解耦（Decoupling）

Attention 的计算公式是点积： $\mathbf{q}^T \mathbf{k}$ 。

我们要实现的相对位置性质是： $Attention(m, n) = g(m-n)$ 。也就是说，结果只能包含 $m-n$ ，不能包含单独的 m 或 n。

加法位置编码的“污染”

假设我们用加法（像 BERT）： $\mathbf{q}' = \mathbf{q} + \mathbf{p}_m$ 。

带入点积公式：

看到那两个交叉污染项了吗？

$\mathbf{q}^T \mathbf{p}_n$ 意思是：“我的查询内容（比如‘苹果’）和绝对位置 $n$ （比如第100个词）的关系”。
这破坏了纯粹的相对性。模型需要花额外的力气（权重）去抵消这些绝对位置带来的噪声，才能学会“只关注前面第 3 个词，不管我们在第 10 句还是第 100 句”。

加法会引入“内容-位置”的交叉噪声，而旋转利用几何性质，在点积中完美保留了相对距离，没有任何多余的项。

2.长文本外推为何失效？（频率与 OOD）

你的直觉可能在想：“训练时见过的长度，模型学会了；没见过的长度，模型就懵了。”

神经网络是“内插（Interpolation）”的高手，却是“外推（Extrapolation）”的白痴

神经网络在训练数据的范围内（Convex Hull）表现很好，一旦跳出这个范围，它的行为是不可控的。

“时钟”比喻（频率视角）

RoPE 的不同维度就像不同转速的时钟指针：

高频维度（秒针）：转得飞快。在训练长度（比如 2048）内，它已经转了几百几千圈了。模型见过它在 0度、90度、180度、270度的所有样子。
低频维度（时针）：转得极慢（这是为了捕捉长距离依赖）。在训练长度 2048 内，它可能只转了 0 到 30 度。

当你推理长度达到 4096 时（外推）：

秒针没事，反正它一直在转圈，模型见过它。
时针转到了 60 度！
模型从未在训练中见过这个维度的向量指向 60 度！ 模型的激活函数、权重矩阵对这个“全新的角度”没有任何准备，输出的数值可能瞬间崩坏（Attention Score 异常大或小），导致生成乱码。

解决方案：插值 (PI, YaRN)

所以现在的长文本技术（如 Llama 3.1 的处理）不是让时针转到 60 度，而是骗模型： “嘿，虽然现在是第 4096 个词，但我把所有的刻度都缩小一半。现在的 4096 当作以前的 2048 来看。” 这样时针还是指在 30 度，模型就觉得“哦，这个我熟”，从而恢复了能力。这叫位置插值 (Position Interpolation)。

一句话总结： 外推失效是因为低频维度旋转到了训练时从未见过的“未知角度区域”（Out-of-Distribution），模型对此没有任何泛化能力。

3.先旋转还是先 Linear？（线性代数与特征语义）

你的直觉可能在想：“反正都是乘法，换个顺序有区别吗？”

1. 数学上的不可交换性

Linear 层是矩阵乘法 $y = Wx$ 。
RoPE 是旋转操作 $x' = Rx$ 。
矩阵乘法一般是不满足交换律的： $W(Rx) \neq R(Wx)$ 。除非 $W$ 是单位矩阵或某种特殊的循环矩阵，但神经网络的 $W$ 是随机初始化并学习出来的杂乱矩阵。

我们要思考 $W$ （Query/Key 的投影矩阵）在学什么？

$W$ 的作用是将 Token 的原始语义（Embedding）映射到 Attention 的特征空间。比如，它提取“名词属性”、“动词属性”等。

如果先旋转 (RoPE -> Linear)：

输入 $x$ 是带着位置信息在转圈的。 $W$ 看到的是一个忽左忽右、一直在变的向量。

$W$ 会很痛苦：“大哥，你一会儿头朝上，一会儿头朝下，我怎么提取特征啊？”

模型必须消耗大量的参数容量去学习“旋转不变性”，这是巨大的浪费。

如果先 Linear (Linear -> RoPE)：

$W$ 先从稳定的 Embedding 中提取出语义特征向量 $\mathbf{q}$ 和 $\mathbf{k}$ 。

然后，RoPE 再给这个特征向量加上位置属性（旋转它）。

最后，Attention 机制比较这两个“带着位置的特征向量”。

这样， $W$ 只需要专注于语义，RoPE 专注于位置，各司其职，效率最高。

2D 图像的陷阱

如果你做 Vision Transformer，想把 RoPE 用在 $(x, y)$ 坐标上。

如果你试图混合旋转（比如三维球体旋转），你会发现先转 X 轴再转 Y 轴，和先转 Y 轴再转 X 轴，结果是不一样的！

这意味着位置编码失去了唯一性。

解决办法：切分维度。前一半维度只编码 $x$ ，后一半维度只编码 $y$ 。让它们互不干扰，各自在自己的子空间里旋转。

一句话总结： Linear 层需要稳定的语义输入来提取特征，先旋转会破坏输入的稳定性；而后旋转则是将提取好的特征安放于时空坐标中，符合逻辑。

第五步：从零实现多头注意力机制

都看到这里了，我默认你们都懂注意力机制哈，今天我讲点和网上不一样的，有兴趣可以看一下

多头注意力机制（Multi-Head Attention, MHA）在数学上本质是：将原有的高维向量空间切分为多个独立的子空间（Subspaces），在不同的子空间内并行地寻找相关性，最后通过线性变换将信息融合。

1. 核心直觉：为何需要“多头”？(The Geometry of Subspaces)

在单个向量 $x \in \mathbb{R}^{d_{model}}$ 中，所有的语义信息（语法、指代、情感、位置）都纠缠（Entangled）在一起。

单头注意力的局限性： 如果只用一组 $W_Q, W_K, W_V$ ，我们实际上是在寻找一种特定的“加权平均”模式。虽然数学上 $W$ 矩阵可以很大，但 Softmax 是“赢家通吃”的（Winner-take-all）。如果一个词既要关注前面的主语（语法关系），又要关注后面的形容词（语义修饰），单头注意力往往会被其中最强的一个关系主导，无法同时捕捉多重关系。

多头的数学意义： 通过不同的投影矩阵，我们将输入向量 $X$ 投影到了 $h$ 个不同的语义子空间。在子空间 $i$ 中，向量可能只编码了“词性”信息；在子空间 $j$ 中，可能只编码了“时态”信息。

结论： 多头注意力不仅仅是“并行计算”，它是为了解决特征解耦（Feature Disentanglement）的问题。

2. 数学推导：从投影到融合

假设输入序列矩阵为 $X \in \mathbb{R}^{L \times d_{model}}$ ，其中 $L$ 是序列长度。

第一步：线性投影（Linear Projections）

这是将高维空间映射到子空间的过程。对于每一个“头” $i$ （i=1, ..., h），我们要学习三组独立的线性变换矩阵：

$W_i^Q \in \mathbb{R}^{d_{model} \times d_k}, \quad W_i^K \in \mathbb{R}^{d_{model} \times d_k}, \quad W_i^V \in \mathbb{R}^{d_{model} \times d_v}$

通常为了计算方便，设 $d_k = d_v = d_{model} / h$ 。

生成的 Query, Key, Value 分别为：

$Q_i = X W_i^Q, \quad K_i = X W_i^K, \quad V_i = X W_i^V$

数学直觉： 这里 X 被旋转、缩放并降维到了 $d_k$ 维度的流形上。每个 $W_i$ 就像是一个滤镜，只允许特定类型的特征通过。

第二步：缩放点积注意力（Scaled Dot-Product Attention）

在每个子空间内，我们计算注意力分数。这是核心的几何操作：

$\text{head}_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}\left(\frac{Q_i K_i^T}{\sqrt{d_k}}\right) V_i$

计算完 $h$ 个头的输出后，我们得到了一组结果。现在需要将它们“缝合”回原来的 $d_{model}$ 空间。

$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O$

其中 $W^O \in \mathbb{R}^{h \cdot d_v \times d_{model}}$ 。

拼接（Concat）： 物理上将各个子空间的信息并列在一起。此时的向量维度恢复为 $L \times d_{model}$ 。
线性变换 $W^O$ ： 这不仅仅是改变维度，它的数学作用是特征混合（Feature Mixing）。它决定了应该采纳哪个头的信息，或者如何组合不同头的信息来形成最终的上下文表示。

3. 为什么多头比单头更强？（低秩瓶颈理论）

这涉及到矩阵的秩（Rank）的概念。

在注意力矩阵 $A = \text{softmax}(\dots)$ 中，如果 $d_k$ 很小（单头情况下 $d_k$ 必须很大），注意力矩阵往往倾向于低秩（即每一行都差不多，或者非常稀疏）。

有研究表明（如 Google 的论文 Low-Rank Bottleneck in Multi-Head Attention），多头机制允许模型构建出具有更高“表达能力”的注意力图。通过拼接多个低秩的注意力头，最终的输出矩阵能够表达更复杂的依赖关系，打破了单头注意力的低秩瓶颈。

提问：

问题1： 假设 $d_k$ （每个头的维度）设置得过小（例如远小于序列长度 $L$ ），注意力矩阵 $A = \text{softmax}(QK^T/\sqrt{d_k})$ 会发生什么数学上的病态现象？这如何解释为什么我们不能简单地用“多而小”的头来无限堆叠？

问题2： 许多简化的实现（甚至某些教科书）会忽略 $W_O$ 或者认为它只是为了调整维度。如果去掉 $W_O$ ，仅仅将多头输出拼接（Concat），模型性能会如何变化？从线性代数的角度看， $W_O$ 究竟是在做一个什么操作，使得“多头”不仅仅是“多个独立的单头”？

问题3： 标准的 Softmax Attention 计算复杂度是 $O(L^2)$ 。如果我们把 $\text{softmax}(Q K^T)$ 看作是一个核函数（Kernel Function） $K(q, k)$ ，我们能否通过 $\phi(Q) \phi(K)^T$ 的形式重写它，从而先计算 $K^T V$ ，将复杂度降为 $O(L)$ ？

1.投影维度的限制导致表达力上限。

数学事实：注意力矩阵 $A$ 的原始形式是 $QK^T$ 。其中 $Q, K \in \mathbb{R}^{L \times d_k}$ 。根据线性代数定理，矩阵乘积的秩不可能超过中间维度：

$\text{Rank}(QK^T) \leq \min(L, d_k)$
推论： 当序列长度 $L$ 很长（例如 4096），而单头的维度 $d_k$ 很小（例如 64）时，注意力矩阵 $A$ 虽然是 $L \times L$ 的，但它是一个极低秩（Low-Rank）矩阵。
后果： 低秩意味着注意力矩阵的行向量是线性相关的。换句话说，模型在 $L$ 个位置上能生成的“注意力模式”是非常有限的。
为何多头能解：虽然每个头都是低秩的，但我们有 $h$ 个头。

$\text{Output} = \sum_{i=1}^h \text{head}_i W_i^O$

多个低秩矩阵的和（或拼接后的线性变换）可以形成一个高秩甚至满秩的矩阵。多头机制本质上是通过集成多个低秩投影来逼近全秩的复杂语义依赖。

2.它是一个“基变换”和“信息路由器”

如果没有 $W_O$ ： 假设直接输出拼接结果 $[h_1, h_2, ..., h_h]$ 。这时的残差连接（Residual Connection）会将这个向量直接加到输入 $X$ 上。这意味着：第 $i$ 个头的输出被迫只能更新嵌入向量中第 $i$ 个切片（slice）的信息。子空间之间是永久隔离的。
线性代数视角： $W_O$ 是一个全连接矩阵。它的作用是：
1. 混合（Mix）： 它允许 Head 1 提取的“主语”信息和 Head 2 提取的“谓语”信息进行加权组合。
2. 重定位（Re-orientation）： 注意力层的输出是一组由 V向量组成的集合。W_O 将这些向量旋转（Rotate）回残差流（Residual Stream）的最佳基（Basis）方向，以便后续的 FFN 层能够最有效地处理它们。
结论： W_O决定了“哪些头的信息更重要”，以及“如何将这些分散的特征整合成统一的语义表示”。

3. 注意力与核方法

标准 Attention： $\text{Softmax}(QK^T)V$ 。这里必须先算 $QK^T$ （ $L \times L$ 矩阵），复杂度 $O(L^2)$ 。
核方法视角：如果我们能找到特征映射 $\phi(\cdot)$ 使得 $\text{Softmax}(q^T k) \approx \phi(q)^T \phi(k)$ ，那么公式变为：

$(\phi(Q) \phi(K)^T) V$
结合律魔法：矩阵乘法满足结合律 $A(BC) = (AB)C$ 。我们可以改变计算顺序：

$\phi(Q) (\phi(K)^T V)$
- 先计算 $\phi(K)^T V$ ：维度是 $(d \times L) \times (L \times d) \rightarrow d \times d$ 。复杂度 $O(L)$ 。
- 再用 $\phi(Q)$ 去乘这个 $d \times d$ 矩阵。
代价： 标准 Softmax 是指数函数，具有极强的聚焦（Focusing）能力（大的更大，小的趋零）。大多数线性核函数（Linear Kernels）如 $1+ELU(x)$ 产生的分布过于“平滑”。在需要精确检索（如“查找第 5 个词”）的任务中，线性 Attention 表现往往不如标准 Attention。

class MyAttention(nn.Module):
    def __init__(self, d_model, n_heads, max_len=2048):
        """
        d_model: 输入向量维度 (如 512)
        n_heads: 注意力头数 (如 8)
        """
        super().__init__()
        assert d_model % n_heads == 0, "d_model 必须能被 n_heads 整除"

        self.d_model = d_model
        self.n_heads = n_heads
        self.head_dim = d_model // n_heads

        # 1. 定义 Wq, Wk, Wv, Wo 投影层
        # 这里使用我们自己写的 MyLinear
        self.w_q = MyLinear(d_model, d_model, bias=False)
        self.w_k = MyLinear(d_model, d_model, bias=False)
        self.w_v = MyLinear(d_model, d_model, bias=False)
        self.w_o = MyLinear(d_model, d_model, bias=False)

        # 2. 初始化 RoPE
        # 注意：RoPE 是作用在每个头的维度上的 (head_dim)
        self.rope = MyRoPE(self.head_dim, max_seq_len=max_len)

    def forward(self, x, kv_cache=None, start_pos=0):
        """
        kv_cache: (past_k, past_v) 之前的记忆
        start_pos: 当前的起始位置 (传给 RoPE 用)
        """
        batch_size, seq_len, _ = x.shape

        # 1. 投影
        q = self.w_q(x).view(batch_size, seq_len, self.n_heads, self.head_dim).transpose(1, 2)
        k = self.w_k(x).view(batch_size, seq_len, self.n_heads, self.head_dim).transpose(1, 2)
        v = self.w_v(x).view(batch_size, seq_len, self.n_heads, self.head_dim).transpose(1, 2)

        # 2. RoPE (传入 start_pos!)
        # Q 和 K 都要旋转，而且必须基于它们在全句中的真实位置
        q = self.rope(q, start_pos)
        k = self.rope(k, start_pos)

        # 3. 处理 KV Cache
        if kv_cache is not None:
            past_k, past_v = kv_cache
            # 拼接：把过去的历史 (past) 和现在算出来的 (k, v) 接在一起
            k = torch.cat([past_k, k], dim=2)
            v = torch.cat([past_v, v], dim=2)

        # 保存最新的 Cache，传给下一次用
        current_cache = (k, v)

        # 4. Attention 计算
        # Q (B, H, 1, D) @ K_total (B, H, Total_Len, D)
        scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(self.head_dim)

        # 注意：使用 Cache 时，Mask 需要稍微变一下
        # 但如果是推理模式 (seq_len=1)，Q 只有一个，K 有很多个
        # 其实不需要 Mask (因为只能看过去，过去全在 K 里)，或者 Mask 逻辑非常简单
        # 这里为了演示简单，我们假设推理时不需要显式传入 mask，因为 K 都是过去的
        if seq_len > 1:
            mask = torch.triu(torch.ones(seq_len, seq_len), diagonal=1).to(x.device)
            scores = scores.masked_fill(mask == 1, float('-inf'))

        attn_weights = F.softmax(scores, dim=-1)
        output = torch.matmul(attn_weights, v)

        output = output.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)

        # 返回 output 和 新的 cache
        return self.w_o(output), current_cache

# --- 测试代码 ---
# attn = MyAttention(d_model=512, n_heads=8)
# x = torch.randn(2, 10, 512) # 2句话，每句10个词
# out = attn(x)
# print(out.shape) # 应该是 (2, 10, 512)
# print("Attention 模块构建成功！")

第6步：transformer层

这里就很简单了，就是我们之前定义的堆叠。：

一、堆叠的基本单元：Transformer Block

虽然我们常说“堆叠注意力层”，但实际上我们堆叠的是一个完整的 Transformer Block（块）。

一个标准的 Transformer Block 包含两个核心子层（Sub-layers）：

多头注意力层（MHA）： 负责处理序列内部的信息交换（提取上下文）。
前馈神经网络（Feed-Forward Network, FFN/MLP）： 负责对特征进行加工和整合（提取非线性特征）。

为了让这个 Block 可以无限堆叠，必须引入两个机制：

残差连接（Residual Connection）： 防止梯度消失。
层归一化（Layer Normalization）： 稳定数值分布。

现在的标准架构（Pre-Norm）

目前的大模型（如 LLaMA, GPT-3）通常采用 Pre-Norm 结构。一个 Block 的数学表达如下：

$x_{attn} = x + \text{Attention}(\text{RMSNorm}(x))$

$x_{out} = x_{attn} + \text{FFN}(\text{RMSNorm}(x_{attn}))$

class TransformerBlock(nn.Module):
    def __init__(self, d_model, n_heads, hidden_dim, max_len):
        super().__init__()

        # 1. Attention 部分
        self.norm1 = MyRMSNorm(d_model)
        self.attention = MyAttention(d_model, n_heads, max_len=max_len)

        # 2. Feed Forward (SwiGLU) 部分
        self.norm2 = MyRMSNorm(d_model)
        self.feed_forward = MySwiGLU(d_model, hidden_dim)

    def forward(self, x, kv_cache=None, start_pos=0):
        # Attention 部分
        _x = self.norm1(x)
        # 把 cache 传进去，接收新的 cache
        attn_out, new_kv_cache = self.attention(_x, kv_cache=kv_cache, start_pos=start_pos)
        x = x + attn_out

        # FFN 部分 (FFN 不需要 cache)
        _x = self.norm2(x)
        x = x + self.feed_forward(_x)

        return x, new_kv_cache

最后组装模型

class MyLanguageModel(nn.Module):
    def __init__(self, vocab_size, d_model, n_layers, n_heads, hidden_dim, max_len=2048):
        """
        组装完整的 Llama 模型
        """
        super().__init__()

        # 1. 嵌入层 (Token Embeddings)
        self.token_embedding = MyEmbedding(vocab_size, d_model)

        # 2. Transformer 层堆叠
        # nn.ModuleList 就像一个普通的 Python List，但是 PyTorch 能识别里面的参数
        self.layers = nn.ModuleList([
            TransformerBlock(d_model, n_heads, hidden_dim, max_len)
            for _ in range(n_layers)
        ])

        # 3. 最终归一化
        # Llama 在输出层之前还会再做一次 Norm，保证输出稳定
        self.norm_final = MyRMSNorm(d_model)

        # 4. 语言模型头 (LM Head)
        # 把 d_model 维度的向量投影回 vocab_size，这样才能预测下一个词是啥
        # bias=False 是 Llama 的习惯
        self.lm_head = MyLinear(d_model, vocab_size, bias=False)

    def forward(self, x, kv_caches=None, start_pos=0):
        """
        kv_caches: 一个列表，列表里存着每一层的 (k, v)
        """
        # 如果是第一次运行，初始化一个空列表
        if kv_caches is None:
            kv_caches = [None] * len(self.layers)

        new_caches = []

        x = self.token_embedding(x)

        # 遍历每一层
        for i, layer in enumerate(self.layers):
            # 取出这一层对应的 cache
            layer_cache = kv_caches[i]

            # 跑这一层
            x, new_layer_cache = layer(x, kv_cache=layer_cache, start_pos=start_pos)

            # 存下这一层的新 cache
            new_caches.append(new_layer_cache)

        x = self.norm_final(x)
        logits = self.lm_head(x)

        return logits, new_caches

您可能感兴趣的与本文相关的镜像