MATLAB实现三天体（三体运动）相互纠缠的混沌运行可视化

最新推荐文章于 2025-11-23 20:38:09 发布

原创最新推荐文章于 2025-11-23 20:38:09 发布 · 614 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言 #三体问题 #物理仿真

数学同时被 3 个专栏收录

15 篇文章

订阅专栏

MATLAB

14 篇文章

订阅专栏

物理

10 篇文章

订阅专栏

## 核心功能
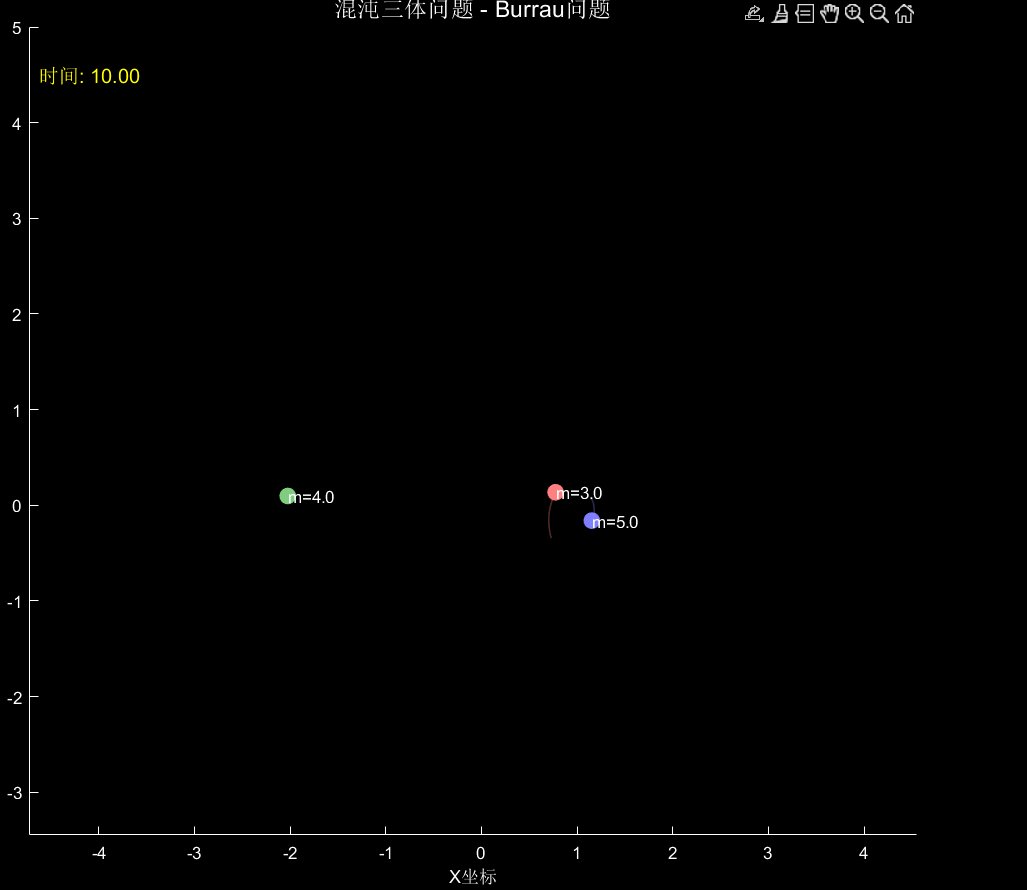
该MATLAB代码实现了**混沌三体系统的数值模拟与可视化**，基于经典的Burrau问题初始条件，展示三个不同质量天体在相互引力作用下的混沌运动。

## 关键特性

### 🔬 物理模型
- **牛顿引力定律**：完整实现三体引力相互作用
- **数值求解**：使用ODE45求解器进行高精度积分
- **质量设置**：三个天体质量比为3:4:5（归一化）
- **初始条件**：Burrau问题设置，从静止状态开始

### 🎯 混沌特征体现
- **不可预测轨迹**：复杂且永不重复的运动路径
- **敏感依赖性**：对初始条件的极端敏感性
- **不规则振荡**：天体间距离的混沌变化
- **长期不可预测性**：确定性系统中的随机行为

### 📊 可视化功能
1. **实时动画**
- 彩色轨迹跟踪显示
- 实时位置更新
- 时间进度显示
- 质量标签动态跟随

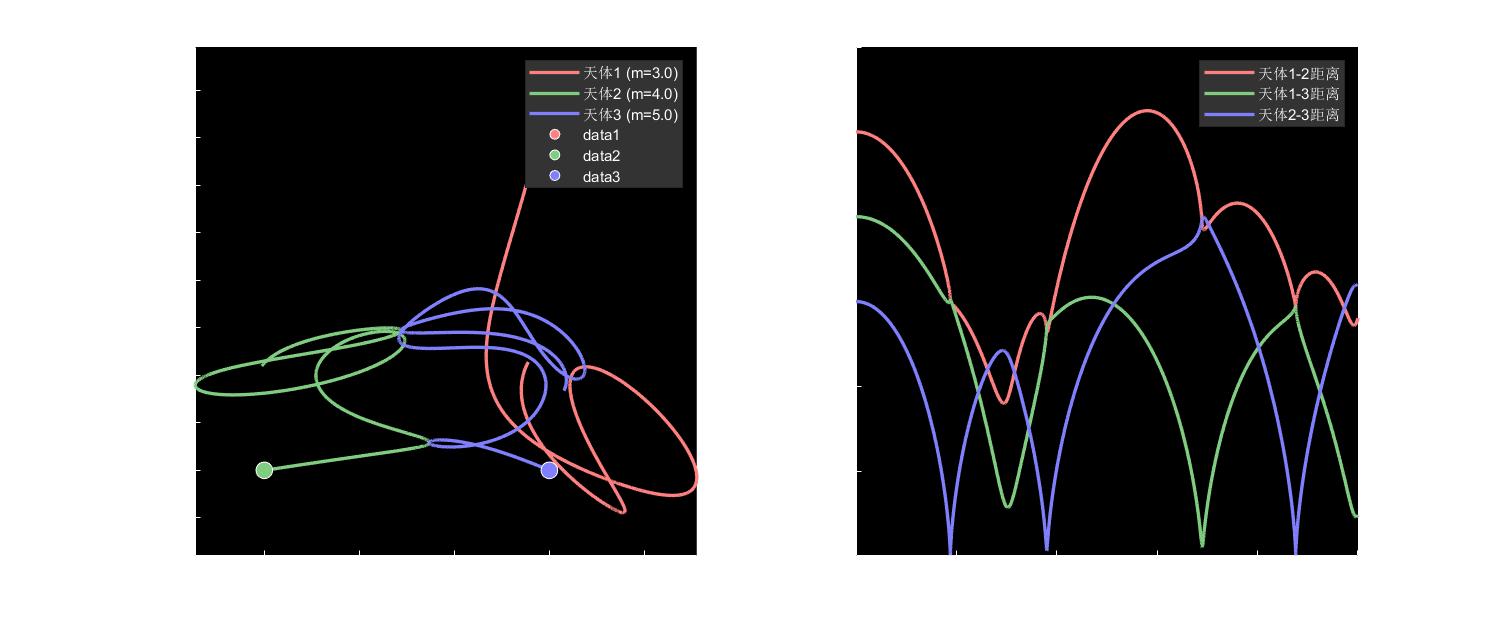
2. **分析图表**
- 完整运动轨迹图
- 天体间距离随时间变化曲线
- 多子图对比分析

### ⚙️ 技术实现
- **坐标系**：二维平面运动模拟
- **时间参数**：可调节模拟时长和步长
- **视觉效果**：黑色背景配合彩色轨迹，优化观察体验
- **性能优化**：跳帧显示和轨迹长度控制

## 科学意义
该代码完美展现了**三体问题的本质特征**：
- 从简单物理定律衍生出极端复杂行为
- 混沌系统中确定性方程产生不可预测结果
- 为理解非线性动力学和混沌理论提供直观示例

## 应用价值
- 天体力学教学演示
- 混沌理论可视化研究
- 数值方法验证
- 复杂系统行为分析

这个模拟生动地再现了《三体》小说中描述的那种"永恒混乱、不可预测"的宇宙环境，将抽象的数学概念转化为直观的视觉体验。

function three_body_chaotic
% 混沌三体问题模拟
% 使用Burrau问题初始条件

clf;
clear;

% 物理常数
G = 1;  % 引力常数 (归一化)

% 三个天体的质量 (归一化)
m = [3, 4, 5];

% 初始位置 - Burrau问题
r0 = [1, 3;    % 天体1 [x, y]
     -2, -1;   % 天体2 [x, y]
     1, -1];   % 天体3 [x, y]

% 初始速度
v0 = [0, 0;    % 天体1 [vx, vy]
     0, 0;     % 天体2 [vx, vy]
     0, 0];    % 天体3 [vx, vy]

% 模拟参数
tspan = [0, 10];  % 时间范围
dt = 0.01;        % 时间步长

% 初始状态向量 [x1,y1,x2,y2,x3,y3, vx1,vy1,vx2,vy2,vx3,vy3]
y0 = [r0(1,:), r0(2,:), r0(3,:), v0(1,:), v0(2,:), v0(3,:)];

% 求解ODE
options = odeset('RelTol',1e-8,'AbsTol',1e-10);
[t, y] = ode45(@three_body_ode, tspan, y0, options, m, G);

% 提取轨迹
r1 = y(:,1:2);
r2 = y(:,3:4);
r3 = y(:,5:6);

% 创建动画
figure('Position', [100, 100, 1000, 800]);
set(gcf, 'Color', 'black');
axis equal;
hold on;

% 设置坐标轴范围
margin = 2;
x_vals = [r1(:,1); r2(:,1); r3(:,1)];
y_vals = [r1(:,2); r2(:,2); r3(:,2)];
xlim([min(x_vals)-margin, max(x_vals)+margin]);
ylim([min(y_vals)-margin, max(y_vals)+margin]);

% 颜色设置
colors = [1, 0.5, 0.5;    % 浅红色
          0.5, 0.8, 0.5;  % 浅绿色
          0.5, 0.5, 1];   % 浅蓝色

% 轨迹线
trace1 = plot(nan, nan, 'Color', [colors(1,:), 0.3], 'LineWidth', 1);
trace2 = plot(nan, nan, 'Color', [colors(2,:), 0.3], 'LineWidth', 1);
trace3 = plot(nan, nan, 'Color', [colors(3,:), 0.3], 'LineWidth', 1);

% 天体点
body1 = scatter(nan, nan, 100, colors(1,:), 'filled');
body2 = scatter(nan, nan, 100, colors(2,:), 'filled');
body3 = scatter(nan, nan, 100, colors(3,:), 'filled');

% 质量标签
text(r0(1,1), r0(1,2), sprintf('m=%.1f', m(1)), 'Color', 'white', 'FontSize', 10);
text(r0(2,1), r0(2,2), sprintf('m=%.1f', m(2)), 'Color', 'white', 'FontSize', 10);
text(r0(3,1), r0(3,2), sprintf('m=%.1f', m(3)), 'Color', 'white', 'FontSize', 10);

title('混沌三体问题 - Burrau问题', 'Color', 'white', 'FontSize', 14);
xlabel('X坐标', 'Color', 'white');
ylabel('Y坐标', 'Color', 'white');
set(gca, 'Color', 'black', 'XColor', 'white', 'YColor', 'white');

% 动画参数
skip_frames = 5;  % 跳帧以提高动画速度
trace_length = 100;  % 轨迹长度

% 动画循环
for i = 1:skip_frames:length(t)
    % 更新轨迹（只显示最近的部分）
    start_idx = max(1, i-trace_length);
    idx_range = start_idx:i;
    
    set(trace1, 'XData', r1(idx_range,1), 'YData', r1(idx_range,2));
    set(trace2, 'XData', r2(idx_range,1), 'YData', r2(idx_range,2));
    set(trace3, 'XData', r3(idx_range,1), 'YData', r3(idx_range,2));
    
    % 更新天体位置
    set(body1, 'XData', r1(i,1), 'YData', r1(i,2));
    set(body2, 'XData', r2(i,1), 'YData', r2(i,2));
    set(body3, 'XData', r3(i,1), 'YData', r3(i,2));
    
    % 更新质量标签位置
    delete(findall(gca, 'Type', 'text', 'String', sprintf('m=%.1f', m(1))));
    delete(findall(gca, 'Type', 'text', 'String', sprintf('m=%.1f', m(2))));
    delete(findall(gca, 'Type', 'text', 'String', sprintf('m=%.1f', m(3))));
    
    text(r1(i,1), r1(i,2), sprintf('m=%.1f', m(1)), 'Color', 'white', 'FontSize', 10);
    text(r2(i,1), r2(i,2), sprintf('m=%.1f', m(2)), 'Color', 'white', 'FontSize', 10);
    text(r3(i,1), r3(i,2), sprintf('m=%.1f', m(3)), 'Color', 'white', 'FontSize', 10);
    
    % 添加时间显示
    time_text = sprintf('时间: %.2f', t(i));
    if i == 1
        time_display = text(min(xlim)+0.1, max(ylim)-0.5, time_text, 'Color', 'yellow', 'FontSize', 12);
    else
        set(time_display, 'String', time_text);
    end
    
    drawnow;
    
    % 暂停以控制动画速度
    pause(0.01);
end

% 绘制最终轨迹
figure('Position', [100, 100, 1200, 500]);
set(gcf, 'Color', 'black');

subplot(1,2,1);
set(gca, 'Color', 'black', 'XColor', 'white', 'YColor', 'white');
hold on;
plot(r1(:,1), r1(:,2), 'Color', colors(1,:), 'LineWidth', 2, 'DisplayName', sprintf('天体1 (m=%.1f)', m(1)));
plot(r2(:,1), r2(:,2), 'Color', colors(2,:), 'LineWidth', 2, 'DisplayName', sprintf('天体2 (m=%.1f)', m(2)));
plot(r3(:,1), r3(:,2), 'Color', colors(3,:), 'LineWidth', 2, 'DisplayName', sprintf('天体3 (m=%.1f)', m(3)));
scatter(r1(1,1), r1(1,2), 100, colors(1,:), 'filled', 'MarkerEdgeColor', 'white');
scatter(r2(1,1), r2(1,2), 100, colors(2,:), 'filled', 'MarkerEdgeColor', 'white');
scatter(r3(1,1), r3(1,2), 100, colors(3,:), 'filled', 'MarkerEdgeColor', 'white');
xlabel('X坐标', 'Color', 'white');
ylabel('Y坐标', 'Color', 'white');
title('三体运动轨迹', 'Color', 'white', 'FontSize', 14);
legend('TextColor', 'white', 'Color', [0.2, 0.2, 0.2]);
axis equal;

subplot(1,2,2);
set(gca, 'Color', 'black', 'XColor', 'white', 'YColor', 'white');
hold on;
% 计算相对距离
dist12 = vecnorm(r1 - r2, 2, 2);
dist13 = vecnorm(r1 - r3, 2, 2);
dist23 = vecnorm(r2 - r3, 2, 2);

plot(t, dist12, 'Color', colors(1,:), 'LineWidth', 2, 'DisplayName', '天体1-2距离');
plot(t, dist13, 'Color', colors(2,:), 'LineWidth', 2, 'DisplayName', '天体1-3距离');
plot(t, dist23, 'Color', colors(3,:), 'LineWidth', 2, 'DisplayName', '天体2-3距离');
xlabel('时间', 'Color', 'white');
ylabel('距离', 'Color', 'white');
title('天体间距离变化', 'Color', 'white', 'FontSize', 14);
legend('TextColor', 'white', 'Color', [0.2, 0.2, 0.2]);

fprintf('模拟完成！\n');
fprintf('系统展现了典型的混沌行为：\n');
fprintf('- 轨迹复杂且不可重复\n');
fprintf('- 对初始条件极其敏感\n');
fprintf('- 距离变化呈现不规则振荡\n');

end

function dydt = three_body_ode(t, y, m, G)
% 三体问题ODE函数
% y = [x1,y1,x2,y2,x3,y3, vx1,vy1,vx2,vy2,vx3,vy3]

% 提取位置和速度
r = [y(1:2)'; y(3:4)'; y(5:6)'];
v = [y(7:8)'; y(9:10)'; y(11:12)'];

% 初始化加速度
a = zeros(3,2);

% 计算每个天体受到的引力
for i = 1:3
    for j = 1:3
        if i ~= j
            r_ij = r(j,:) - r(i,:);
            r_norm = norm(r_ij);
            a(i,:) = a(i,:) + G * m(j) * r_ij / (r_norm^3);
        end
    end
end

% 组装导数向量
dydt = zeros(12,1);
dydt(1:6) = [v(1,:), v(2,:), v(3,:)]';      % 速度
dydt(7:12) = [a(1,:), a(2,:), a(3,:)]';    % 加速度

end